Une courbe peut être vue dans sa globalité comme un objet statique, mais aussi comme la trajectoire d'un point se mouvant dans l'espace. De la dynamique à la cinématique, les courbes permettent de représenter naturellement les mouvements des corps, des astres les plus volumineux aux particules les plus minuscules ou aux rayons lumineux.
Un autre lien entre théorie et pratique est matérialisé par les systèmes mécaniques, ces assemblages parfois étonnants que l'on peut utiliser pour tracer les courbes.
LES ARTICLES
Les liens entre mathématiques et sciences physiques sont anciens et profonds. Ils se matérialisent de manière privilégiée sous la forme des courbes, trajectoires et autres lieux géométriques obtenus par l'expérience. Les coniques sont particulièrement présentes, et ce à toutes les échelles, du microscopique au macroscopique.
Les propriétés géométriques des cycloïdes et des trochoïdes ont mis des décennies avant d'être mises au jour. Les savants qui les ont étudiées se sont d'abord posées des questions physiques ou pratiques, avant de se lancer dans l'examen de ces courbes remarquables.
Les roulettes n'épuisent pas les possibilités offertes par le mouvement plan sur plan, ni les merveilles géométriques qui s'y cachent. Toujours munis d'une feuille de papier à dessin, d'un calque et de stylos, l'exploration se poursuit avec des courbes un peu oubliées, les glissettes.
Étonnamment, il est possible d'adapter les profils de roue et de route pour que l'axe de la roue reste à hauteur constante, pour le plus grand confort du voyageur.
Du papier à dessin, du papier calque, des crayons de couleur, un peu de curiosité et d'astuce pratique... Vous voici armés pour partir à la rencontre des roulettes et pour redécouvrir un classique aujourd'hui oublié de la géométrie dynamique, le mouvement plan sur plan.
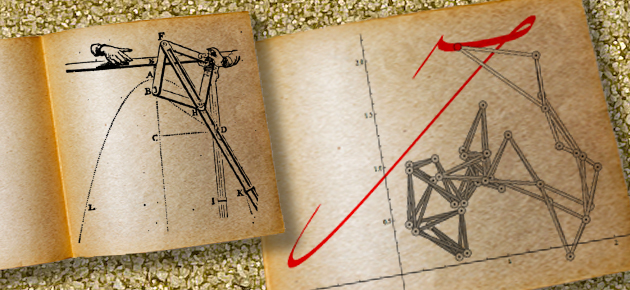
Machines à tracer
Jean-Jacques Dupas
Si l'on considère les courbes comme des lieux géométriques, de tout temps on a utilisé des instruments, voire des machines, pour les tracer sur un support matériel. Les assemblages mécaniques conçus permettent effectivement de représenter fidèlement la courbe étudiée.
En bref : Dévier la trajectoire d'un astéroïde ?
Bertrand Hauchecorne
Une équipe internationale a pour mission d'étudier la possibilité de dévier la trajectoire d'astéroïdes en cas de risque de collision avec la Terre.
En bref : Améliorer le record du 200 m grâce aux maths !
Bertrand Hauchecorne
Et si les records de vitesse pouvaient être améliorés en changeant la forme des pistes d'athlétisme ?