Les débuts de la cycloïde

Dans l’Antiquité, Archimède définissait « sa » spirale par deux mouvements (voir « Les spirales ») et il l’étudiait de manière géométrique. Dans les années 1630, la cycloïde et la trochoïde étaient vues comme des trajectoires et étudiées de manière cinématique. La cycloïde (voir « Des roues et des routes adaptées ») donna lieu à l’invention de méthodes fructueuses puis servit de banc d’essai aux nouvelles méthodes infinitésimales. Les mathématiciens ont associé beaucoup de propriétés géométriques aux deux courbes, mais montré aussi qu’elles répondent à des phénomènes de la nature, ce qui les rend étonnantes.

Mersenne et le paradoxe de la roue

Dans les années 1620, Marin Mersenne s’intéresse au paradoxe de la roue du pseudo-Aristote, à savoir que deux cercles parcourent des espaces proportionnels à leurs diamètres, tandis qu’ils parcourent un même espace s’ils sont solidaires et de même centre.

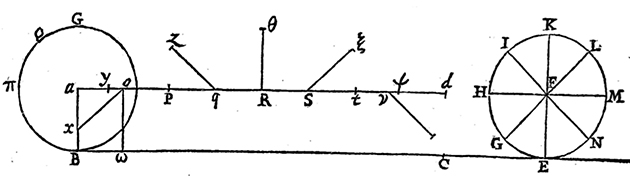
Il envisage le paradoxe en se demandant quelle est la courbe parcourue par un point de la circonférence d’un cercle qui roule. Il écrit dans ses Questions inouïes de 1634 que c’est « la moitié d’une ellipse », mais il questionne Gilles de Roberval sur cette réponse. Comment savoir si la courbe est ou non une ellipse ? En janvier 1637, Roberval lui répond en donnant une construction de la courbe par points (voir la figure ci-dessous) et en annonçant que « cette ligne n’est ni ellipse, ni pas une des lignes courbes que nous trouvons dans les livres ; qu’au contraire elle a ses propriétés à part, que je décrirais toutes, si j’avais assez de loisir ».

La construction de la cycloïde par points de Roberval.
Figure extraite de [1].

Il est alors en possession de résultats sur l’aire sous une arche et sur la tangente qui lui permettent d’affirmer que la cycloïde n’est pas l’une des courbes déjà étudiées. Apprenant par Mersenne les résultats de Roberval, René Descartes et Pierre de Fermat se lanceront à leur tour à l’assaut de la cycloïde.

Pour déterminer la tangente à la cycloïde, Roberval introduit une méthode qui sera publiée par l’Académie des sciences en 1693 dans les Observations sur la composition des mouvements et sur le moyen de trouver les touchantes aux lignes courbes. Son « principe d’invention » s’appuie sur le cas du cercle pour affirmer que « la direction du mouvement d’un point qui décrit une ligne courbe est la touchante [la tangente] de la ligne courbe en chaque position de ce point-là ». La méthode est donc cinématique : une courbe est la trajectoire d’un point en mouvement et la tangente est la direction du mouvement au point considéré. Pour trouver une tangente en un point d’une courbe, il faut donc examiner « les divers mouvements du point qui la décrit et composer tous ces mouvements en un seul ».

Dans le cas de la cycloïde, la tangente est facile à déterminer puisqu’elle est définie comme une trajectoire : un point de la courbe E est soumis à un mouvement horizontal [EF) et à un mouvement de rotation dont la direction est la tangente (EP) du cercle qui roule. Il écrit que « les deux mouvements sont égaux » puisque la base AC de la cycloïde est égale à la circonférence du cercle, et il construit la bissectrice de l’angle \( \widehat{\mathrm{PEF}}\)  pour obtenir la tangente.

La méthode de Roberval pour déterminer la tangente à la cycloïde.  Le lecteur remarquera une erreur dans la représentation de la bissectrice. Figure extraite de [1].

Roberval applique cette règle à toutes les courbes, nouvelles ou anciennes, étudiées à son époque. Pour cela, il faut d’abord redéfinir les courbes comme des trajectoires.

Dans la Géométrie de 1637, Descartes a fourni une méthode algébrique pour déterminer les tangentes aux courbes algébriques. On peut imaginer son embarras lorsque Mersenne lui apprend que son ennemi Roberval a trouvé la tangente à la cycloïde, puisque cette courbe est une « courbe mécanique » (ou « transcendante » aujourd’hui). Dans une lettre à Mersenne d’août 1638, il emploie donc un autre moyen que sa méthode des tangentes.

La méthode de Descartes. Figure extraite de [5].

Descartes fait rouler un polygone

La démonstration est « fort courte et fort simple », écrit-il. Il fait rouler un polygone rectiligne, par exemple un hexagone, alors la courbe est composée des arcs de cercles  \( \widehat{\mathrm{EH}},\, \widehat{\mathrm{HI}},\,\, \widehat{\mathrm{IA}}.\)  Donc la normale (c’est-à-dire la perpendiculaire de la tangente) en chacun des points de cette courbe est le rayon de l’arc de cercle correspondant. Pour l’arc de cercle  \( \widehat{\mathrm{HI}}\) , la normale en un point est la droite qui joint ce point au point G, point de contact de l’hexagone « qui roule » sur la base (ED). En considérant la cycloïde « comme un polygone qui a une infinité de côtés », il conclut que la normale en un point B de la cycloïde est (BO), où O est le point de contact du cercle sur la base (AD). Le point O est construit en considérant le demi-cercle de diamètre CD, (BN) parallèle à (AD) et (BO) parallèle à (ND).

Dans les années 1580, Galilée avait eu l’idée de réguler les horloges en leur adaptant un pendule car il croyait qu’un pendule est isochrone (c’est-à-dire que le temps de descente à la position verticale est le même, quelle que soit l’amplitude). Il est démenti par Mersenne en 1636.

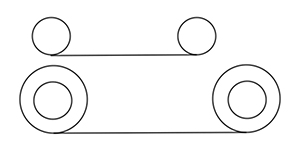
En 1656, Huygens cherche à construire une horloge pour déterminer la longitude d’un bateau en mer, afin de bien conserver l’heure du port de départ du bateau pour pouvoir la comparer avec l’heure à bord. Pour obtenir un pendule isochrone, il commence par faire osciller un pendule entre deux lames de métal, puis en 1659, il démontre que les lames doivent avoir exactement la forme d’arcs de cycloïde (voir Un monde d’oscillations, San Vu Ngoc, Tangente 179, 2017).

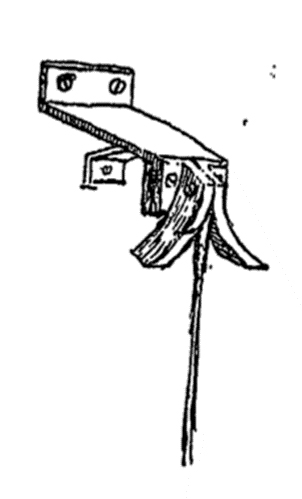
Le pendule est fixé entre deux lames de métal de forme cycloïdale.
Figure extraite de [2].

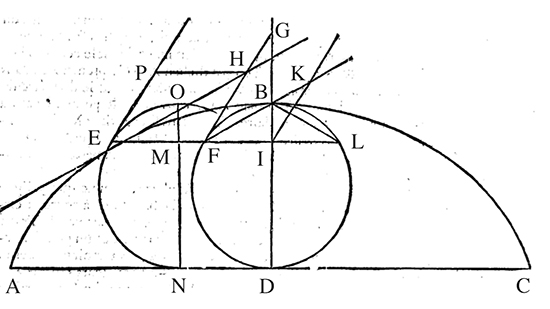
Huygens présente son pendule isochrone dans son traité Horologium Oscillatorium de 1673. Dans la partie II, il démontre que la cycloïde est tautochrone, c’est-à-dire que les temps de descente sur une pente cycloïdale sont égaux, quel que soit le point de départ sur la cycloïde. Puis, dans la partie III, il démontre que si un pendule oscille entre deux lames de métal ayant la forme de deux demi-cycloïdes alors l’extrémité du pendule décrit une cycloïde, ce qui assure l’isochronisme du pendule. Cette partie est consacrée à sa « théorie des développées et des développantes ». Étant donnée une courbe AB appelée développée, on considère pour tous les points D de AB une portion de tangente CD de longueur égale à la portion de courbe DA. La courbe parcourue par l’extrémité C est la développante de AB. La proposition I énonce que toute tangente (DC) à la développée AB est une normale à la développante (voir la figure ci-dessous).

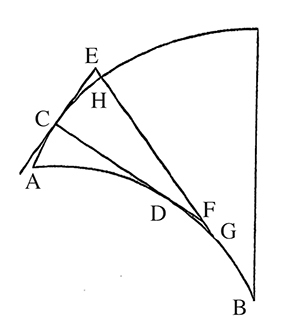
Développées et développantes. Figure extraite de [2].

Dans la proposition V, Huygens démontre que la développante de la demi-cycloïde AC est une demi-cycloïde AF qui lui est égale (voir la figure ci-dessous). Pour cela il utilise la propriété de la tangente obtenue par Descartes et la « propriété spécifique » de la courbe donnée par Pierre de Fermat en 1638, à savoir que, pour tout point B de AC, le segment [HB] est égal à l’arc de cercle  \( \widehat{\mathrm{AH}}\) . Il se demande alors si d’autres courbes sont égales à leurs développantes. La réponse sera donnée en 1729 par George Wolfgang Krafft (1701–1754), qui montre que la cycloïde et la spirale logarithme sont les deux seules courbes à posséder cette propriété.

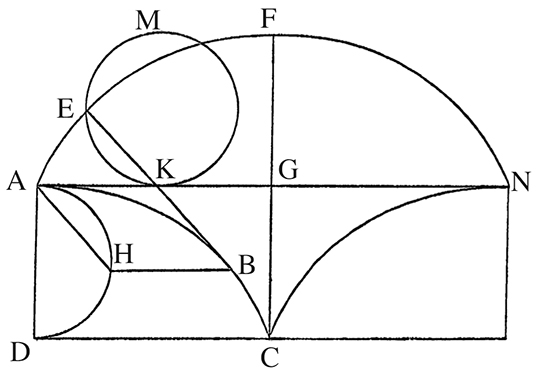
Illustration de la démonstration de la proposition V de Huygens. Figure extraite de [2].

Avec le calcul infinitésimal

Dans un mémoire de 1684 intitulé Nouvelle Méthode pour chercher les maxima et les minima, ainsi que les tangentes, Leibniz divulgue son calcul infinitésimal. Il y considère que « dans son principe, trouver la tangente consiste à tracer une droite joignant deux points infiniment proches de la courbe, c’est-à-dire tracer le côté d’un polygone infinitangulaire qui équivaut à la courbe ». Sa méthode a l’avantage de s’appliquer aux courbes transcendantes, comme il l’explique en 1686 en leur associant une équation, dite aujourd’hui différentielle. Il prend l’exemple d’une courbe transcendante qui a beaucoup occupé les géomètres : la cycloïde. Il part de la « propriété spécifique » de la cycloïde, et, en supposant que le cercle est de rayon l’unité et en notant  \( \widehat{\mathrm{NC}}=a,\)  MP = y et PB = x, il obtient y = sin a + a et x = 1 – cos a.

L’équation différentielle de la cycloïde d’après [3].

Il en déduit que dx = sin a da, donc  \( a=\int \frac{dx}{\sin a}=\int \frac{dx}{\sqrt{2x-x^2}}.\)  

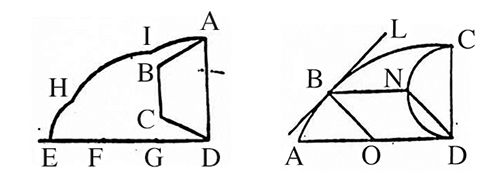
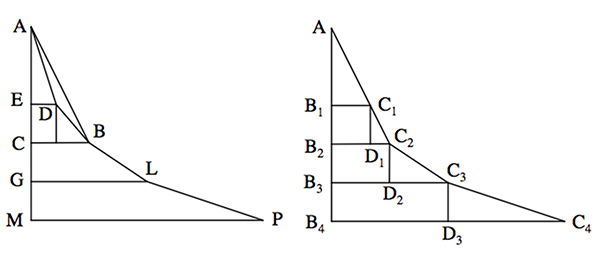
Dans un prospectus de juin 1696, Jean Bernoulli pose aux géomètres le problème de trouver « la courbe la plus rapide » pour descendre entre deux points de hauteurs différentes ; il l’appelle « brachistochrone », par référence à la « tautochrone » de Huygens. Leibniz « tombe sous son charme » et il donne une solution dans une lettre à Jean : pour qu’une trajectoire soit la plus rapide, elle doit être composée de portions infinitésimales qui soient les plus rapides. Le problème est donc ramené à trouver un polygone brachistochrone ABLP (voir la figure ci-dessous). Pour cela, il fait varier un point D horizontalement et il cherche le temps de descente minimum sur ADB. D’après l’étude sur les plans inclinés de Galilée, si r et n sont les temps de descente le long de [AE] et [EC], alors les temps de descente t_AD et t_DB le long de [AD] et [DB] sont tels que :
  \( t_{\mathrm{AD}}=r\frac{\mathrm{AD}}{\mathrm{AE}}\,\, \hbox{et}\,\, t_{\mathrm{DB}}=n\frac{\mathrm{DB}}{\mathrm{EC}}.\)

Leibniz additionne les deux temps de descente pour obtenir le temps cumulé sur ADB, il différencie selon ED et il écrit que le résultat doit être nul pour obtenir un minimum : 
\( \frac{r}{\mathrm{AD}}\frac{\mathrm{ED}}{\mathrm{AD}}- \frac{n}{\mathrm{EC}}\frac{\mathrm{FB}}{\mathrm{DB}}=0.\)

Le polygone brachistochrone de Leibniz. D’après [3].

En prenant pour dx les segments [D_n-1C_n] et pour dy les segments [C_nD_n], il obtient une équation :  \( \frac{dy}{dx}=\sqrt{\frac{x}{2-x}}.\)

Dans sa lettre, Leibniz n’indique pas que cette équation est celle d’une cycloïde alors qu’elle est celle d’une symétrique de la développée de la cycloïde examinée en 1686, qui est  \( \frac{dy}{dx}=\sqrt{\frac{2-x}{x}}.\)

Mais il le montre en 1697, en exhibant une belle propriété géométrique de la courbe. Jean Bernoulli résout à son tour le problème par analogie avec un rayon lumineux qui se réfracte et il reconnaît la cycloïde. Ensuite son frère Jacques trouve une autre solution. La brachistochrone frappe les esprits : comment imaginer que la courbe la plus rapide ne soit pas la plus « simple », la droite ?

La forme des vagues

Les trochoïdes sont les trajectoires d’un point à l’intérieur d’un cercle qui roule sur une droite ou d’un point à l’extérieur attaché au cercle. Elles sont étudiées dans les années 1630 et seront appelées d’abord respectivement cycloïdes raccourcies et cycloïdes allongées  (voir « Des roues et des routes adaptées »).

Le phénomène de la houle est remarqué par Leonard de Vinci dans son livre Del moto e di mesura de l’acqua, parce que le mouvement de l’eau se propage sans qu’il y ait translation de masses comme « l’ondulation que fait le vent dans les blés sans que les blés aient changé de place ». Dans ses Principia de 1687, Isaac Newton examine le mouvement des particules dans un fluide, et un siècle plus tard, Pierre-Simon de Laplace et Joseph-Louis Lagrange essaient de déterminer ce mouvement. Une première « théorie des vagues » est donnée par Franz Josef von Gerstner dans le mémoire Theorie der Wellen, paru à Prague en 1804. Adhémar Barré de Saint-Venant le fait connaître en France en publiant sa traduction en français en 1887 ; il explique que Gerstner se place dans le cas de vagues simples, régulières et également espacées, comme celles de la houle par temps calme, avec des sommets et des creux paraissant se transporter transversalement avec une vitesse constante, les particules d’eau ne faisant que glisser entre elles.

Gerstner considère un point A au-dessous de la surface de l’eau et la ligne AMN constituée de tous les points où la pression est la même qu’en A, ce qui correspond à une ligne de niveau. Il prend (AQ) l’horizontale qui lui est tangente en A et il mène par un point M la perpendiculaire (MP) à (AQ). Il note la ligne AM = s, AP = x, PM = y et g la vitesse qu’une chute libre fait acquérir aux corps en une seconde. Il considère v la vitesse de M suivant la direction MN, dM la force de gravité en M, qui se décompose selon la tangente (MD) et la normale (ME), et R le rayon de courbure au point M.

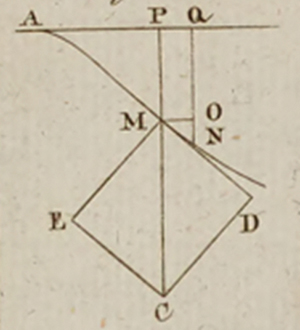
Par définition de la ligne AMN, il faut que la pression  \( \frac{d\mathrm{M}}{ds}\Big(\frac{dx}{ds}-\frac{v^2}{g\mathrm{R}}\Big)\)  soit constante. Étant donnés R₀ le rayon de courbure et v₀ la vitesse au point A, il introduit, pour simplifier les calculs, m et d tels que  \( \frac{1}{m}=\frac{g}{v^2_0}-\frac{1}{\mathrm{R}_0}\)  et  \( d=\frac{2m^2}{\mathrm{R}_0}.\)  Puis il considère le cercle ERB de diamètre d, avec B le point le plus bas, et  \( \varphi\)  l’angle  \( \widehat{\mathrm{ECR}}\) . Il calcule les vitesses horizontale et verticale de M et il obtient respectivement :
\( v\frac{dx}{ds}=\frac{mg}{v_0}-\frac{mv_0}{\mathrm{R}_0}\cos\varphi \,\,\hbox{et}\,\, v\frac{dy}{ds}=\frac{mv_0}{\mathrm{R}_0}\sin\varphi .\)
Il intègre ces équations et il aboutit à
\( y\frac{m^2}{\mathrm{R}_0}(m-\cos\varphi) \,\,\hbox{et}\,\, x\frac{m^2g}{v^2_0}\varphi-\frac{m^2}{\mathrm{R}_0}\sin\varphi.\)
Gerstner en déduit que AMB est une trochoïde, dont il calcule l’abscisse et l’ordonnée.

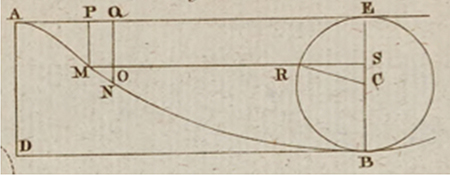
Figure extraite de [4].

Gerstner écrit que « la simplicité, que la nature garde dans tant d’autres phénomènes, sera encore, ici, l’objet de notre admiration ». Sa théorie sera complétée par la suite en incluant le cas où le fond de l’eau n’est pas à une distance infinie, notamment par Tullio Levi-Civita en 1925 et par Marie-Louise Dubreil-Jacotin dans sa thèse soutenue à l’université de Paris en 1934.