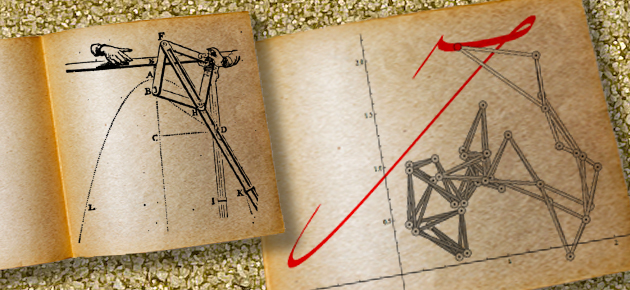
La courbe la plus simple est la droite ; on utilise la règle pour la tracer (voir la Droite, Bibliothèque Tangente 59, 2017). Pour le cercle, on utilise le compas (voir le Cercle, Bibliothèque Tangente 36, 2009). Les Grecs ont utilisé d’autres courbes comme la cissoïde de Dioclès, la conchoïde de Nicomède ou la quadratrice d’Hippias pour résoudre des problèmes tels la quadrature du cercle ou la trisection de l’angle (voir article « Des courbes pour dépasser le compas »). En s’attelant à la duplication du cube, Ménechme, au IV e siècle avant notre ère, découvrit la triade « ellipse, hyperbole, parabole ». Ce sera surtout Apollonius de Perge, contemporain d’Archimède, qui rendra ces courbes célèbres sous le nom de « coniques ». Existe-t-il des machines pour tracer des coniques ?
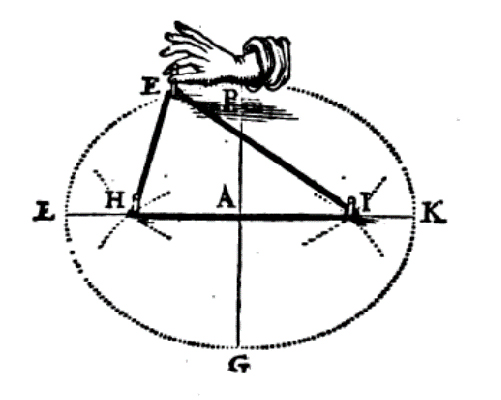
Le tracé d’une ellipse par la méthode du jardinier.
Pour les coniques...
Pour tracer une ellipse, on peut utiliser l’ellipsographe d’Archimède (voir Mathematical Models, Henry Martyn Cundy et Arthur Percy Rollett, Oxford University Press, 1961), aussi appelé trammel d’Archimède dans la littérature anglo-saxonne (trammel signifiant « entrave », on a avec cette terminologie une référence explicite aux deux rainures prismatiques du mécanisme). Ce mécanisme est-il l’œuvre d’Archimède, au III e siècle avant notre ère ? C’est peu plausible, aucun texte de lui n’attestant de cette construction. Par contre, c’était un fin mécanicien ; il est probable qu’il ait rencontré Ctésibios le fondateur de l’école de mécanique d’Alexandrie.
De même, Proclus (412 – 485) a bien cité la propriété des ellipses qui aurait pu conduire à la construction mécanique de l’ellipsographe, mais là encore les preuves font défaut. Pour la première construction avérée d’une telle machine, il faut attendre le marquis de l’Hôpital (1661 – 1704). Un exemplaire de son ellipsographe se trouve au musée des sciences de Florence.
De nombreux mécanismes vont servir à tracer des coniques. Frans van Schooten (1615 – 1660) publie plusieurs constructions en 1646 dans son De Organica Conicarum Sectionum. Il commence par la méthode du jardinier pour l’ellipse. Puis il construit la conique grâce au losange OIPG de point fixe I (foyer de l’ellipse) quand P tourne autour de I ; le point courant est donné par l’intersection des droites (HG) et (OP).
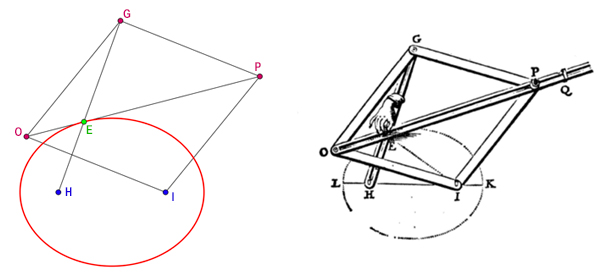
La construction de van Schooten de l’ellipse.
Pour la construction de l’hyperbole, le losange DMFL est articulé au point fixe F. Quand D tourne autour de F, l’intersection des droites (CD) et (LM) donne le point courant de l’hyperbole.
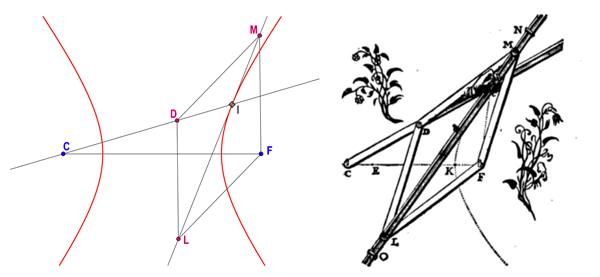
La construction de van Schootende l’hyperbole.
Enfin, pour la construction de la parabole, le losange FGHB est articulé autour du point fixe B. Quand la règle [AD] glisse perpendiculairement à elle-même, l’intersection de la droite (FH) et (AG) donne le point courant D.
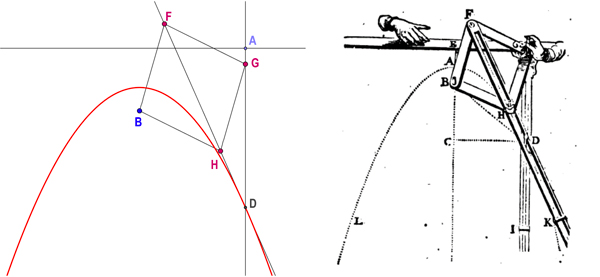
La construction de van Schooten de la parabole.
Barres articulées et pivots
L’invention de la machine à vapeur relance l’intérêt pour ces mécanismes et va permettre la création de la cinématique (l’étude des mouvements). Un piston poussé par la vapeur se déplace en ligne droite, et l’on voudrait récupérer un mouvement circulaire (ou réciproquement obtenir un mouvement linéaire à partir d’un mouvement circulaire). De nombreux mécanismes vont être inventés.
En 1876, le mathématicien britannique Alfred Bray Kempe (1849 – 1922) montre que non seulement on peut tracer des droites avec des systèmes articulés mais que toute courbe algébrique continue peut être tracée avec un mécanisme de type système articulé (c’est-à-dire composé de barres rigides reliées entre elles par des articulations). De plus, le théorème de Weierstrass affirme que toute courbe continue est approchée par un polynôme (voir le dossier « Les polynômes du quotidien », Tangente 193, 2020). De fait, toute courbe continue peut être générée avec un système articulé !
Comment Kempe s’y prend-il ? Il transforme les coordonnées cartésienne x et y de la courbe f (x, y) = 0, où f est un polynôme des deux variables x et y, en coordonnées polaires r et θ. La fonction f peut alors être exprimée en sommes de cos(θ ), cos(2θ ), cos(3θ )… Grâce à des parallélogrammes et des parallélogrammes croisés, Kempe construit des multiplicateurs (dispositifs qui transforment θ en nθ, avec n un entier), des additionneurs et des translateurs. La combinaison astucieuse de ces mécanismes permet la construction de la courbe ! C’est la magie du théorème d’universalité de Kempe. Le regretté mathématicien américain William Thurston (1946 – 2012) l’aurait résumé, lors d’une conférence, par : « Si votre signature est une suite continue de courbes, alors il existe un mécanisme pouvant exécuter votre signature ! »
Ce théorème extraordinaire est trop peu connu. Car s’il assure l’existence d’un mécanisme, et que la démonstration fournit une méthode pour en construire un, celui-ci est toujours excessivement sophistiqué. Aucun résultat ne permet à ce jour de déterminer le mécanisme le plus simple.
Notre chance par rapport à Kempe est que l’informatique peut nous aider. Aussi, Matteo Gallet, Christoph Koutschan, Zijia Li, Georg Regensburger, Joseph Schicho et Nelly Villamizar, dans leur article Planar linkages following aprescribed motion (2015, disponible en ligne), proposent un nouvel algorithme en se restreignant aux courbes paramétriques. Prenant au mot Thurston, ils ont mis au point un mécanisme de vingt-six barres et trente-sept articulations qui trace le « J » de la signature de John Hancock, premier signataire de la Déclaration d’indépendance des États-Unis en 1776.
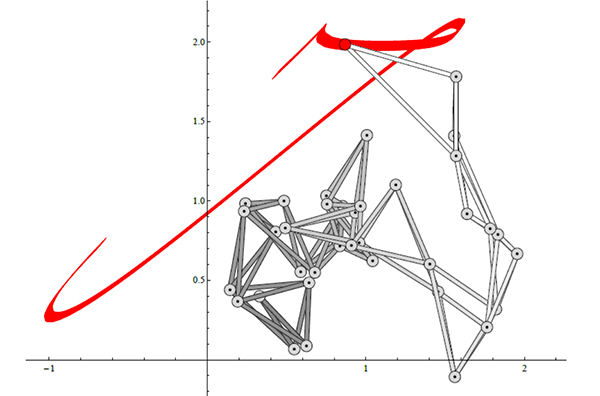
Le mécanisme traçant le J de la signature de John Hancock.
Les systèmes articulés n’en finissent pas d’inspirer les mathématiciens ! Les travaux de Kempe ont trouvé une nouvelle jeunesse chez Thurston. Les informaticiens élaborent des méthodes pour générer automatiquement les mécanismes appropriés aux courbes qui les inspirent. Cela devrait avoir des répercutions, notamment en robotique !
Lire la suite