
La géométrie a ses beautés et ses surprises. Qui penserait que, quelle que soit la forme d’une route, il est possible d’adapter la circonférence d’une roue de façon que son moyeu reste à hauteur fixée ? Inversement, étant donnée une roue, de forme aussi sophistiquée soit-elle, on peut trouver une route qui confère à la roue cette propriété. Bien entendu, il est interdit de tricher : après un (ou plusieurs) tours de roue, la route doit présenter la même configuration ; autrement dit, elle doit être périodique.
La quadrature du cercle ?
La roue polygonale la plus simple est la roue carrée. Comme un carré est constitué de quatre segments, il est naturel d’examiner le cas d’une droite qui « roule » sur une route. La forme de cette route est alors une chaînette (inversée), c’est-à-dire la courbe d’une chaîne tenue à ses deux extrémités (voir article « Paraboles et chaînettes »). L’équation de la chaînette est y = (e x + e – x ) / 2. Le mathématicien américano-canadien Stanley Wagon (né en 1951), l’un des géomètres qui ont contribué à la résolution de ce problème, a réalisé « en vrai » un tel couple roue et route.

Stan Wagon chevauchant courageusement un vélo à roues carrées.
Comme la roue tourne, utilisons les coordonnées polaires pour la paramétrer, ρ et θ variant en fonction du temps t utilisé comme paramètre : ρ = f (t) et θ = g (t). La route est également paramétrée par le temps t : x = h (t), y = k (t). Supposons enfin que l’axe de la roue parcourt l’axe des abscisses x, avec, au temps 0, x (0) = 0 et θ (0) = – π / 2.
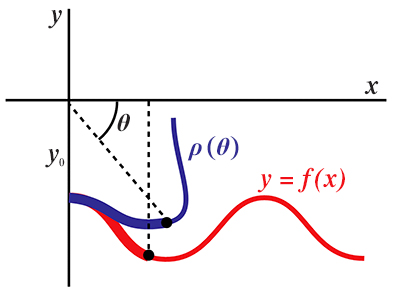
La géométrie roue−route et le repère privilégié.
Dans le mouvement plan sur plan de la roue sur la route (voir article « Gracieuses roulettes »), le plan mobile est associé à la roue et la roulante est le plan immobile. Le centre instantané de rotation du mouvement est au point de contact de la roue avec la route, et comme le mouvement de l’axe doit être horizontal, la vitesse instantanée de l’axe est horizontale, donc la hauteur de l’axe par rapport à la route est égale au rayon ρ. On a donc ρ (θ (t)) = –y (t).
Comme la roue roule sans glisser, pour toutes les valeurs du paramètre t, la longueur s(t) de la route de 0 à t est égale à la longueur de l’arc de roue de θ (0) à θ (t).
Il s’ensuit que l’élément de longueur du pourtour de la roue en coordonnées polaires
ds 2 = ρ 2dθ 2 + dρ2 est égal, sur la route, à dx 2 + dy 2.
Comme ρ(θ (t)) = − y (t), on a dρ = – dy, soit dρ 2 = dy 2.
On en déduit dx 2 = ρ 2 dθ 2, et l’on choisit dx = ρ dθ ; les deux équations dx = ρ dθ et
y = – ρ permettent d’obtenir le paramétrage de la route à partir de celle de la roue
( ρ = f (t) et θ = g(t)), à savoir x = F(t) où F est une primitive de f g’ et y = – f (t).
Route pour une roue en forme de droite
Prenons l’équation d’une droite en coordonnées polaire, ρ = 1/sin θ, avec θ variant entre π et 0 ; on a donc f (t) = 1/sin t et g (t) = t. Une primitive F de f g’ est
Cela semble compliqué ?
En fait non, car
se simplifie en
On obtient
Dans le cas général, bien sûr, pour une route donnée, il peut y avoir plusieurs formes de roues possibles (par exemple, sur les figures F et G ci-dessous, la route est une cycloïde).
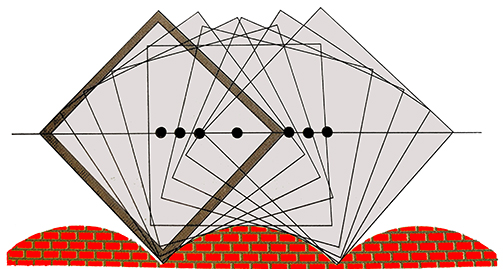
(A) Roue carrée sur une chaînette.
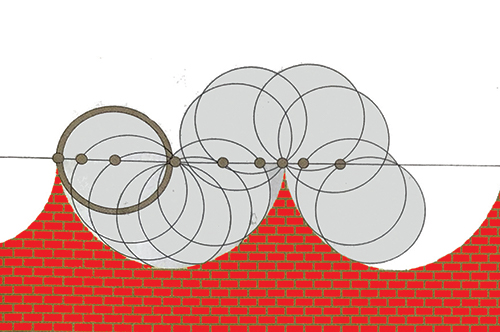
(B) Route circulaire pour roue où le moyeu est sur le pourtour.
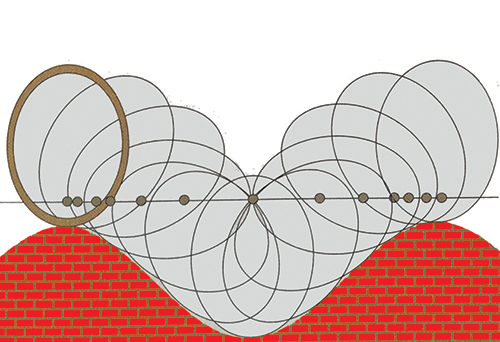
(C) Route sinusoïdale pour roue elliptique.
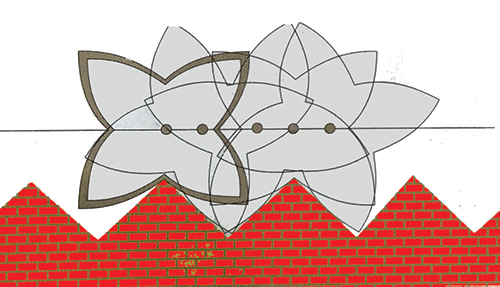
(D) Route en créneau pour roue en spirale à quatre branches.
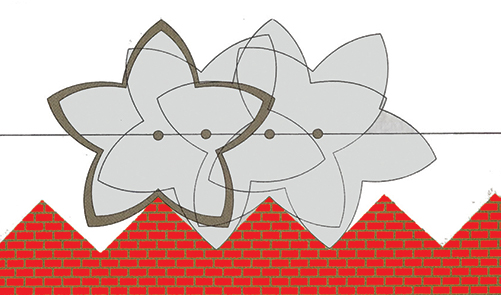
(E) Route en créneau pour roue en spirale à cinq branches.
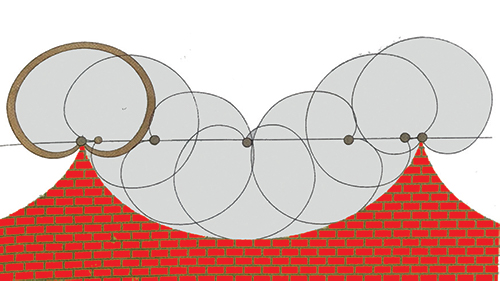
(F) Route cycloïdale pour roue en forme de cardioïde.
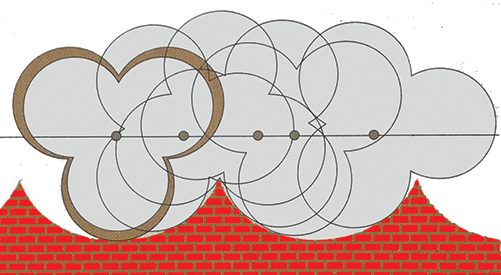
(G) Route cycloïdale pour roue en forme de trèfle.
On peut se demander s’il existe une roue et une route ayant toutes deux la même forme. La réponse (positive) est donnée sur le site d’Alain Esculier indiqué en bibliographie, avec des roues en arcs de cercles pour des routes elles-mêmes en arcs de cercles. Ces résultats étaient-ils connus en théorie des engrenages ?
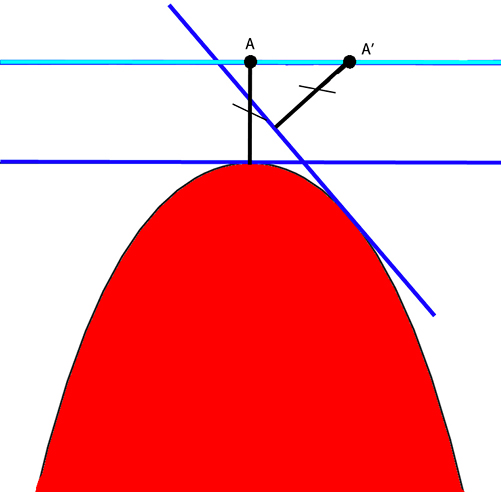
La « roue » (en bleu foncé) roule sans glisser sur une chaînette inversée et son axe parcourt une droite horizontale (en bleu clair).
Lire la suite