Fixez une feuille blanche et posez dessus une feuille de papier calque que vous pouvez déplacer à volonté en la faisant glisser : vous avez la matérialisation de ce que l’on appelle un mouvement plan sur plan.
Marquez maintenant un point fixe M = M(t) sur le calque (le point traceur) et regardez sa trace sur la feuille de papier au cours du temps t. Cette trace s’appelle une roulette. Pourquoi donc ?
Les centres de rotation
Entre deux instants t et t’ le calque (le plan mobile) subit un déplacement qui est une rotation ou une translation. Dans le premier cas, il y a un point fixe, le centre de rotation I (t, t’), et dans le deuxième, on peut considérer qu’il y en a aussi un, à l’infini dans la direction perpendiculaire à celle de la translation.
Lorsque t’ tend vers t, le centre de rotation courant I (t, t’) tend vers le point I(t), dit centre instantané de rotation du mouvement plan sur plan.
Ces différents centres instantanés de rotation décrivent une courbe sur la feuille blanche, et une courbe sur le calque. Supposons maintenant que ces deux courbes soient tracées à l’avance sur les deux feuilles : on constaterait alors que la courbe du calque « roule sans glisser » sur la courbe fixe. D’un point de vue technique, les deux courbes s’appellent respectivement base et roulante ; on les dénommera aussi route et roue de manière plus imagée.
Pour se représenter ce qu’est un roulement sans glissement, on peut imaginer que la route et la roue sont revêtues de minuscules « dents » qui s’engrènent les unes dans les autres. On comprend maintenant mieux l’appellation « roulette », qui résulte du roulement d’une « roue » sur une « route ».
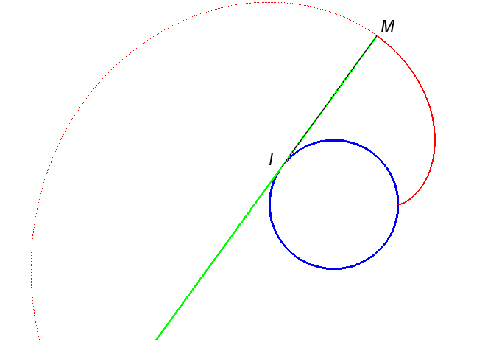
Enfin, le point fixe du calque a une position M = M(t) sur la feuille blanche à l’instant t. La courbe décrite par M(t) sur la feuille blanche est la roulette. Or, le centre de la rotation qui fait passer de la position à l’instant t à la position à l’instant t’ se trouve sur la médiatrice de [M(t), M(t’)]. En faisant tendre t’ vers t, on obtient un résultat très utile : la tangente à la roulette décrite par M(t) est constamment perpendiculaire à la droite (I(t), M(t)), appelée la normale de Chasles.
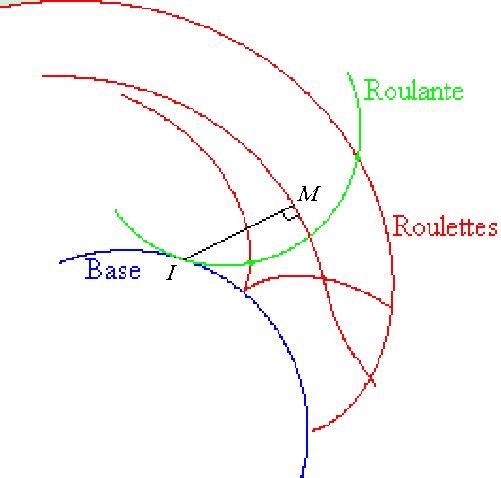
La base (ou route) est en bleu, la roulante (ou roue) est en vert, les roulettes sont figurées en rouge.
Un moyen de réaliser un mouvement plan sur plan est donc de faire rouler deux courbes l’une sur l’autre, chacune emmenant un plan avec elle.
La route la plus simple est la droite, et la roue la plus simple, le cercle. Si l’on choisit comme point traceur M(t) un point du cercle, la roulette est une courbe bien connue : la cycloïde. Elle a pour équations x (t) = R(t − sin t) et y (t) = R(1 − cos t), où R est le rayon de la roue.
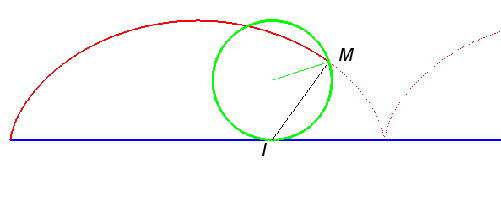
Roulette du point d’un cercle roulant sans glisser sur une droite. La trochoïde obtenue est une cycloïde. (IM) est la normale de Chasles.
Dans le cas d’un point traceur situé à l’intérieur ou à l’extérieur du cercle, on obtient une cycloïde raccourcie, ou une cycloïde allongée. On appelle trochoïde (du grec trokhos, « roue ») l’une de ces trois courbes obtenues en traçant le mouvement décrit par un point lié à un disque qui roule sans glisser sur une droite.
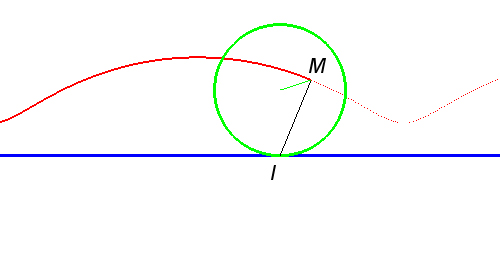
Roulette du point situé à l’intérieur d’un cercle roulant sans glisser sur une droite. La trochoïde obtenue est une cycloïde raccourcie.
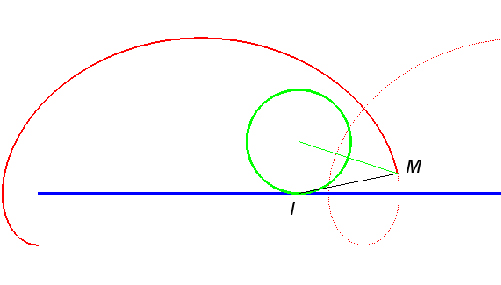
Roulette du point situé à l’extérieur d’un cercle roulant sans glisser sur une droite. La trochoïde obtenue est une cycloïde allongée.
Dans le cas d’une route et d’une roue toutes deux circulaires, les roulettes sont des épitrochoïdes (ou hypotrochoïdes, voir article « Les débuts de la cycloïde »).
Pour une roue elliptique sur route rectiligne, avec le point traceur situé sur la roue, la cycloïde est légèrement déformée.
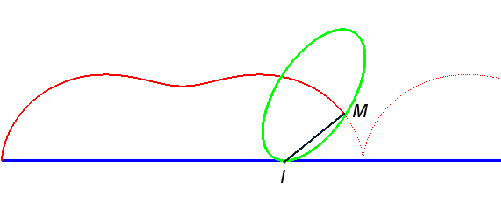
Roulette à base rectiligne obtenue à partir du petit sommet d’une ellipse.
Ça roule !
De fait, la roue peut être une courbe quelconque. Voici par exemple le cas d’une spirale logarithmique sur une route rectiligne. La roulette, avec le centre de la spirale comme point traceur, est alors remarquable : c’est une droite, mais elle n’est pas parallèle à la base !
À l’opposé de cette « roue » dont la courbure varie de 0 à l’infini, on peut considérer une roue rectiligne. La roulette d’un point de la « roue » s’appelle alors une développante de la courbe-route. Par exemple, pour une route circulaire, on peut imaginer qu’un fil enroulé est déroulé en le tendant.
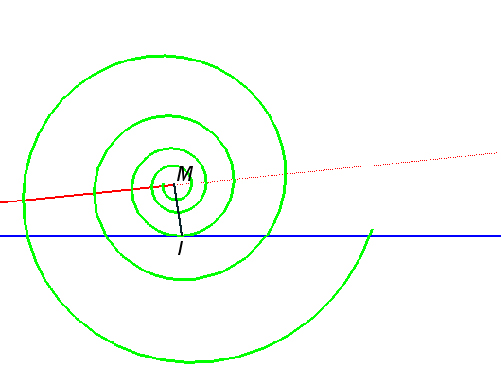
Roulette à base rectiligne obtenue à partir du centre d’une spirale logarithmique.
Développante de cercle : roulette à base circulaire obtenue à partir d’un point d’une « roue » rectiligne.
Parmi les trois courbes en présence (route, roue et roulette), si deux d’entre elles sont connues, la troisième est alors complètement déterminée. Jusqu’à présent, on se donnait la roue et la route, et on en déduisait les roulettes correspondantes. Le problème de la détermination de la route pour une roue donnée est tout aussi intéressant. De même, imposer qu’une roulette soit rectiligne pour une route fixée à l’avance est l’occasion de créer d’étranges véhicules (voir article « Des roues et des routes adaptées »)...

La dualité base−roulante
Mettons-nous à la place d’un « habitant » du papier calque. Il voit, lui, la feuille blanche se déplacer, et pour lui, la base, c’est ce que l’on a appelé la roulante, et vice versa. Le point traceur de la roulette reste fixe dans son plan, mais on pourrait imaginer un point se déplacer dans le calque, qui tracerait une courbe dans la feuille blanche.
La bonne situation générale pour une dualité est donc la suivante : un plan P2 (mobile) se déplace par rapport à un plan P1 (fixe), de sorte qu’une courbe fixe C 2 (la roulante) de P2 roule sans glisser sur une courbe fixe C 1 (la base) de P1. Un point M 2 de P2 se déplace au cours du mouvement, laissant une trace M 1 dans P1. Si M 2 est fixe dans P2, la courbe de M 1 est une roulette ; les courbes parcourues par M 1 et M 2 généralisent donc la notion de roulette.
Si maintenant on échange la base et la roulante, on obtient le mouvement plan sur plan dual du précédent. Par construction, les deux roulettes vont alors s’échanger aussi.
Pour l’illustrer, considérons de nouveau le mouvement d’un cercle sur une droite, et supposons que le point traceur (M 2 ) se déplace à vitesse constante sur un diamètre du cercle. La courbe (M1 ) qu’il trace sur le plan fixe a un petit air de cycloïde qui se déforme du cas raccourci au cas allongé.
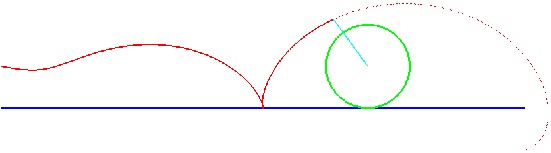
Trace d’un point se déplaçant à vitesse constante sur un diamètre d’un cercle roulant sans glisser sur une droite.
Il est possible de donner les équations de cette courbe étrange : x (t) = t (1 − k sin t), y (t) = (1 − k cos t), k étant la vitesse de propagation sur le diamètre.
Le mouvement dual est celui d’une droite roulant sur un cercle, emmenant un plan avec elle. Et les deux « roulettes » qui s’échangent par dualité sont le diamètre du cercle et cette « pseudo cycloïde ».