Modéliser les trajectoires

Les sciences physiques ont vocation à expliquer, voire à prévoir les phénomènes naturels. L’observation de ces derniers peut suffire à s’émerveiller. Leur explication remplit de satisfaction. Leur prédiction illumine… ou affole. Une autre source d’étonnement continu réside dans la formidable adéquation entre les mathématiques – qui ont leur vie propre – et la physique. Cette fructueuse rencontre entre les deux disciplines peut se faire à travers leurs courbes et leurs trajectoires. Comment une même courbe permet-elle de décrire des mouvements d’objets aussi divers que des particules électriquement chargées ou des planètes ? Comment un sinus peut-il si bien rendre compte des chemins empruntés par la lumière ?

Particules, projectiles et planètes

En sciences physiques, les coniques décrivent toutes les trajectoires… ou presque ! Que l’on modélise une planète ou une comète gravitant autour d’une étoile, un projectile peu soumis à des frottements, ou bien une particule chargée s’approchant d’une autre ou se déplaçant dans un champ électrique uniforme, la trajectoire obtenue est une conique.

Toute interaction mécanique modélisable par une force centrale est susceptible de conduire à une trajectoire elliptique, parabolique ou hyperbolique. On qualifie ainsi les forces dont la direction est la droite passant par les centres des deux objets O₁ et O₂ en interaction, c’est-à-dire du type  \( \overset\to{F}=f(r)\overset\to{e_r}, \)  où  \( \overset\to{e_r} \) est un vecteur directeur de la droite (O₁O₂). En fait,  \( \overset\to{e_r} \)  est aussi un vecteur de la base polaire attachée à l’un des objets étudiés (au point M) et centrée sur l’autre avec lequel il est en interaction (en O). C’est le cas de la force de gravitation entre deux masses et de la force électrostatique entre deux charges électriques.

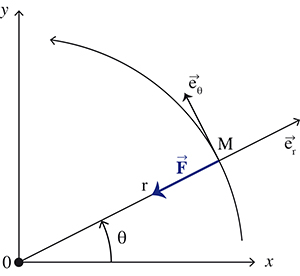
Si l’on peut négliger les autres actions mécaniques subies par ces masses ou ces charges, en raisonnant par conservation de l’énergie mécanique et en s’appuyant sur la loi des aires (une autre loi de conservation des mouvements à force centrale), on obtient des trajectoires d’équation \( r=\frac{p}{1+e\cos(\theta-\theta_0)}\) avec  \( p=\frac{m\mathrm{C}^2}{k}\)  où C est la constante des aires, et  \( e=\sqrt{\frac{2m\mathrm{E}_m\mathrm{C}^2}{k^2}+1},\)  où E_m est l’énergie mécanique de l’objet en mouvement.

Cette écriture correspond à l’équation polaire d’une conique dont l’un des foyers est l’origine du repère. La constante e est son excentricité et u₀ indique la direction de son grand axe. Pour e < 1, la courbe est une ellipse ; pour e = 0, c’est un cercle ; pour e = 1, c’est une parabole ; enfin, pour e > 1, c’est une hyperbole. Ce résultat est connu empiriquement pour les planètes depuis 1609 et la première loi de Kepler : les planètes du système solaire ont un mouvement elliptique autour du soleil. L’explication donnée plus tard par Newton, qui a su introduire la force de gravitation, a l’intérêt de l’expliquer. Elle a aussi permis de prévoir la réapparition dans le ciel d’un autre type d’objet : la comète de Halley. Elle permet enfin de comprendre qu’on ne pourra jamais revoir dans le système solaire d’autres comètes, à mouvement parabolique ou hyperbolique, qui ne sont que déviées par le Soleil.

Ce type de modélisation permet également d’expliquer la déviation de particules chargées. Ainsi, tels des comètes, des noyaux projetés en direction d’autres noyaux peuvent avoir un mouvement hyperbolique. C’est notamment ce qui a permis de comprendre la déviation des noyaux d’hélium projetés sur une feuille d’or lors de l’expérience d’Ernest Rutherford (1909). Quelques « projectiles » parviennent à traverser la feuille d’or, sont déviés par les noyaux d’or et suivent une trajectoire hyperbolique. L’analogie « particules chargées » – « objets célestes » s’arrête cependant là. Un modèle planétaire des atomes dans lequel les électrons auraient un mouvement elliptique autour du noyau ne résiste pas aux effets quantiques sous-jacents.

Dans un champ uniforme

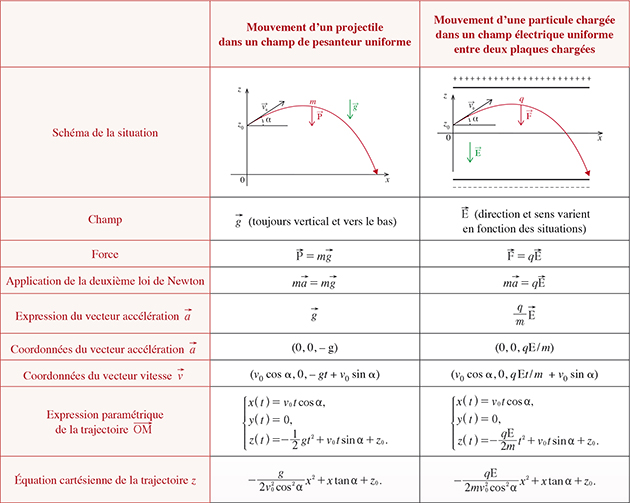
On retrouve les coniques, et plus précisément les paraboles, dans des situations de mouvement dans un champ uniforme. C’est par exemple le cas de projectiles envoyés à la surface de la Terre et peu soumis à l’action de l’air, ou de particules chargées dans un champ électrique uniforme (comme dans les canons à électrons ou dans des accélérateurs et des dispositifs de déviation de particules chargées). Dans ce cas, c’est plutôt l’expression paramétrique de la trajectoire qui est utilisée ou son équation cartésienne. On l’obtient en appliquant la deuxième loi de Newton (tableau ci-dessous).

Les chemins de la lumière

Une autre belle rencontre entre mathématiques et physique a lieu dans le domaine de l’optique. Derrière des illusions d’optique comme celle de la paille « cassée » dans un verre ou à l’origine de la dispersion de la lumière par un prisme se trouve un même phénomène : la réfraction de la lumière. Dans un milieu homogène, un rayon lumineux se propage en ligne droite. Mais quand il change de milieu (quand il passe de l’eau à l’air par exemple, ou de l’air au verre), ce rayon change de trajectoire.

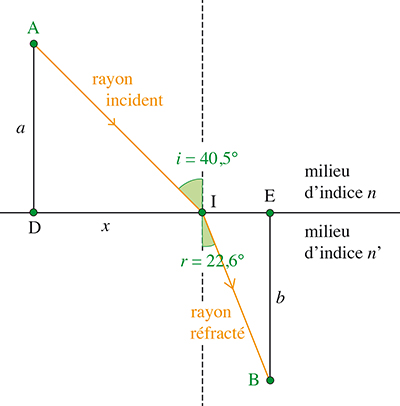
Réfraction de la lumière à l’interface de deux milieux d’indices n et n’ différents.

Ce changement de direction est bien modélisable par la loi de la réfraction de Snell–Descartes, qui lie les angles faits par ces rayons avec la perpendiculaire à la surface de séparation des milieux traversés via la relation n sin (i) = n’ sin (r). Comment une loi aussi simple peut-elle aussi bien rendre compte d’un phénomène physique qui n’est tout de même pas tout à fait trivial ?

L’explication réside dans le changement de vitesse de la lumière quand celle-ci change de milieu. Dans le vide, la vitesse de la lumière c est approximativement égale à 300 000 km/s. Dans un milieu matériel transparent, sa vitesse v est plus faible et vaut \( \frac{c}{n},\)  ce qui définit l’indice de réfraction n du milieu. Par exemple, dans le verre, la vitesse de la lumière n’est « que » de 200 000 km/s environ (soit n = 1,5). Pourquoi un rayon lumineux « change-t-il de direction » quand il change de milieu ? Parce qu’il cherche à minimiser son temps de parcours ! La réfraction lumineuse, c’est une question de plus court chemin, ou de parcours le plus bref.

Pour retrouver ce résultat, on peut paramétrer la situation comme sur le schéma. Un rayon dit incident se propage en ligne droite dans un premier milieu, dont l’indice est n, à la vitesse  \( v=\frac{c}{n}.\) Il arrive dans un second milieu, d’indice n’, en un point d’incidence I, en faisant un angle i avec la normale au plan de séparation entre les deux milieux. Le rayon réfracté se propage dans le second milieu dans une direction différente, faisant un angle r avec la normale précédente, à la vitesse  \( v'=\frac{c}{n'}.\) Le calcul de la position du point I pour que le temps de parcours entre un point A du premier milieu et un point B du second milieu soit le plus bref possible nous conduit alors à la loi de Snell–Descartes (voir encadré).

[encadre]

 La loi de Snell–Descartes

Soit x la distance entre la projection D du point A sur le plan de séparation entre les deux milieux et le point I. Le temps de parcours t de la lumière entre les points A et B est une fonction de x, définie sur [0, DE] et peut se décomposer en deux durées, correspondant aux temps de parcours dans le premier milieu et dans le second :  \( t=f(x)=t+t'=\frac{\mathrm{AI}}{v}+\frac{\mathrm{IB}}{v'},\)

d’où
\( t=\frac{\sqrt{a^2+x^2}}{v}+\frac{\sqrt{b^2+(\mathrm{DE}-x)^2}}{v'}.\)

La fonction f ainsi définie est dérivable sur l’intervalle [0, DE]. On recherche le minimum de cette fonction en étudiant sa dérivée, qui est égale à  \( f'(x)=\frac{x}{v\sqrt{a^2+x^2}}+ \frac{x-\mathrm{DE}}{v'\sqrt{b^2+(\mathrm{DE}-x)^2}}.\)

La dérivée est continue. Or, f ’(0) < 0 et f ’ (DE) > 0. L’équation f ’(x) = 0 possède donc au moins une solution. On en cherche une en introduisant les angles i et r ;
on a x = a tan (i) et DE – x = b tan (r). L’équation f ’(x) = 0 s’exprime alors ainsi :
\( \frac{(\text{tan}\,i)}{v\sqrt{1+\text{tan}^2i}}- \frac{(\text{tan}\,r)}{v'\sqrt{1+\text{tan}^2r}}=0.\)  

Or,  \( 1+\text{tan}^2\alpha=\frac{1}{\cos^2\alpha},\)     et les cosinus des angles étant dans ce cas positifs, on arrive à  \( \frac{(\text{tan}\,i)(\cos i)}{v}- \frac{(\text{tan}\,r)(\cos r)}{v'}=0,\)  soit encore  \( \frac{\sin i}{v}-\frac{\sin r}{v'}=0.\)

Comme  et  le plus bref chemin parcouru par la lumière est tel que les angles i et r vérifient la relation n sin (i) = n’ sin (r).

[/encadre]

Une illusion décryptée

Sur la photo, on a l’impression que la paille est cassée. Sur un schéma vu du dessus du verre et de la paille, on représente un faisceau de rayons lumineux provenant de la paille. Ceux-ci se propagent dans l’eau, puis dans l’air (l’effet de la traversée du verre est négligeable), avant de pénétrer dans l’œil de l’observateur. À l’interface eau–air, ces rayons sont réfractés ; ils changent donc de direction. La partie immergée de la paille semble alors se trouver dans une position différente de la partie hors de l’eau.

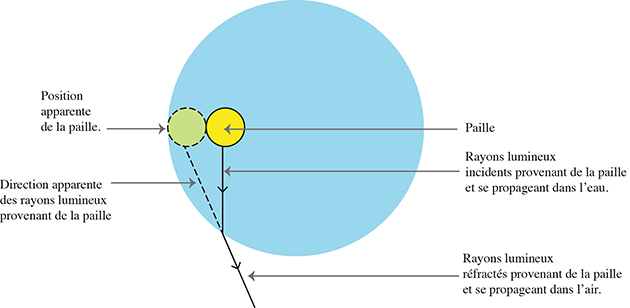
Une paille dans un verre vue du dessus.
À l’interface entre l’eau et l’air, les rayons lumineux provenant de de la paille sont réfractés, ce qui confère à la partie immergée de la paille une position apparente différente de sa partie hors de l’eau et crée l’illusion d’une paille « cassée ».

Il existe évidemment bien d’autres chemins, courbes et trajectoires dans le quotidien du physicien. Ces lieux géométriques se trouvent notamment dans le domaine expérimental, où ils sont parfois mis en évidence à l’aide de capteurs. Ils permettent ainsi d’exposer de manière visuelle des résultats de mesure.