
Les roulettes permettent de se représenter le mouvement relatif du point d’une feuille de papier calque sur une feuille de papier à dessin (voir article « Gracieuses roulettes »). Le mouvement plan sur plan permet en fait d’aller un peu plus loin !
Traçons deux courbes C1 et C2 (les bases de glissement) sur la feuille blanche, et deux autres courbes C’1 et C’2 (les glissantes) sur le calque. Pour obtenir un point M1 de C1, on déplace le calque de sorte que C1 et C’1 soient tangentes, puis on fait glisser C’1 sur C1, qui reste fixe, jusqu’à ce que C2 et C’2 deviennent tangentes (si c’est possible). En déplaçant M1, on obtient un mouvement plan sur plan où C1 est astreinte à rester tangente à C’1 et C2 à C’2. Les roulettes obtenues s’appellent alors plutôt des glissettes. Le centre instantané de rotation I, permettant d’obtenir base et roulante, est à l’intersection des perpendiculaires aux points de tangence.
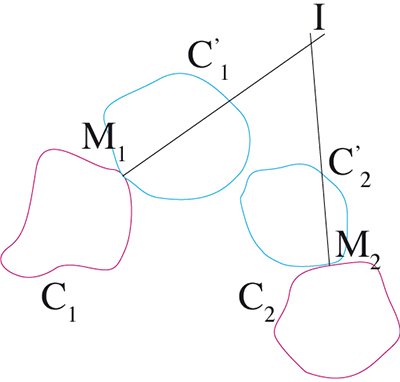
Les bases de glissement sont en mauve, les glissantes en bleu.
De l’art de bien manier son calque
Un cas particulier suffit déjà à illustrer la richesse géométrique des glissettes. Lorsqu’il a été proposé de déplacer un papier calque sur une feuille blanche, comment avons-nous procédé (par la pensée probablement, mais c’est encore plus parlant avec une vraie feuille de papier et un authentique papier calque) ? Peut-être en tenant le calque à deux endroits, pour lui imprimer à la fois un mouvement de translation et de rotation.
On aurait pu aussi tracer deux courbes C1 et C2 dans la feuille blanche et deux points M1 et M2 sur le calque, de sorte à faire décrire à M1 et M2 respectivement les courbes C1 et C2, tout au moins en partie. Il s’agit en fait de ce qui vient d’être décrit, dans le cas où les deux glissantes sont réduites aux points M1 et M2 !
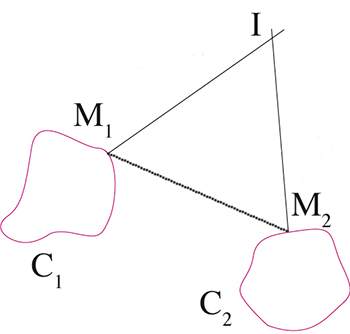
Quand les deux glissantes sont réduites aux points M1 et M2.
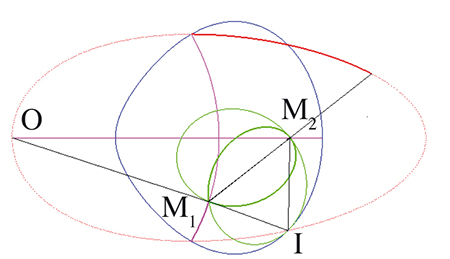
Prenons le cas où les deux courbes C1 et C2 sont des droites, supposées sécantes (réfléchissez à ce que l’on obtient pour des droites parallèles…). Autrement dit, les deux extrémités d’une barre sont astreintes à se déplacer en ligne droite, et la barre emmène avec elle un plan : que dessinent les points de ce plan ? Eh bien, ce sont des ellipses ! Voir ci-dessous le cas où les deux droites sont perpendiculaires ; les deux bases de glissement sont en mauve, et cinq glissettes ont été tracées : celle du milieu de M1 et M2, qui donne un cercle, et quatre autres, dont les points traceurs sont sur la droite (M1M2) et sur la médiatrice de [M1 M2], qui engendrent des ellipses (choisies de sorte à produire une figure symétrique). La base de roulement, en bleu, et la roulante, en vert, sont des cercles. Il s’agit en quelque sorte de la réciproque de la propriété de La Hire, selon laquelle lorsqu’un cercle roule à l’intérieur d’un cercle de rayon double, les points de ce cercle décrivent des segments de droite. Quant à la construction de l’ellipse par cette méthode, il s’agit de la méthode dite « de la bande de papier » (voir Tangente 167, 2015).
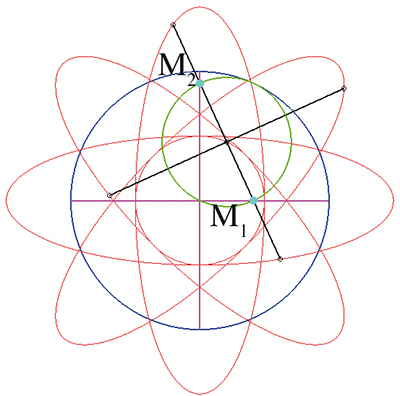
Le cas de deux droites (en mauve) perpendiculaires.
[encadre]
Philippe de La Hire, touche-à-tout de génie
Né en 1640 à Paris, Philippe de La Hire est le fils d’un artiste peintre. Souhaitant suivre les traces paternelles, il se rend à Rome en 1660 pour y étudier la peinture. Il se prend de passion pour les sciences, principalement l’astronomie et les mathématiques, avec un intérêt particulier pour le fonctionnement de différents mécanismes et de leur conception géométrique. Son approche de l’architecture sur des bases scientifiques est elle aussi tout à fait novatrice.
Très influencé par l’architecte et géomètre Girard Desargues (1591–1661), il s’intéresse à la perspective, si utile pour sa peinture, et publie en 1675 un ouvrage sur les sections coniques avec des approches nouvelles sur leurs propriétés projectives.
Il introduit différentes courbes, calcule en 1708 la longueur de la cardioïde et se passionne pour les carrés magiques. En cartographie, on lui doit la projection globulaire, qui se fait par rapport à un point situé sur l’axe polaire à la distance R sin (45°) au-dessus du pôle (où R est le rayon de la Terre). Son nom reste attaché à un théorème qu’il énonce dans son traité des roulettes publié en 1706 : le point d’un cercle de rayon R roulant intérieurement sur un cercle de rayon 2R décrit un diamètre de ce dernier.
Élu en 1678 à l’Académie royale des sciences, La Hire obtient en 1683 la chaire de mathématiques du Collège royal, à laquelle s’ajoute en 1687 celle d’architecture à l’Académie royale. Ce personnage fascinant aura touché à presque toutes les disciplines lorsqu’il s’éteint à Paris en 1718. B.H.
[/encadre]
Les glissettes associées se compliquent nettement pour des bases de glissement circulaires. On les désigne par courbes du trois-barres, car le mouvement est obtenu à partir de trois barres articulées attachées à deux points fixes, les deux centres des cercles. La base et la roulante du mouvement ne semblent pas être des courbes connues par ailleurs.
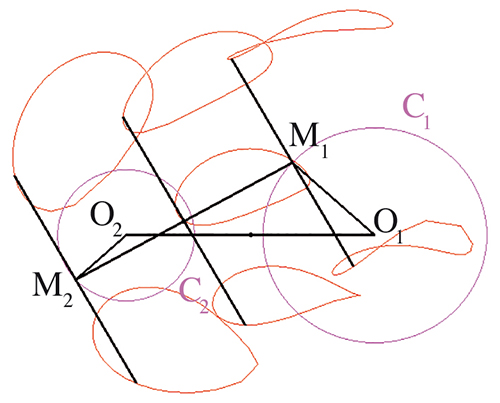
La partie centrale d’une barre articulée O1M1M2O2 emmène un plan avec elle.
Bielle et manivelle
Prenons le cas de deux bases de glissement, l’une rectiligne, l’autre circulaire (dans la figure suivante, on a pris le cas particulier où le cercle est centré sur la droite). On peut imaginer une barre articulée O1M1M2 fixée en O, le point M2 étant astreint à se déplacer rectilignement. Les deux parties de cette barre double s’appellent respectivement la manivelle et la bielle.
On obtient le point I, centre instantané de rotation, par intersection des deux perpendiculaires aux bases de glissement en M1 et M2. La roulante est une élégante courbe à deux points doubles, dite courbe de Jérabek.
Ce mouvement est connu des ferrovipathes, car il est réalisé par exemple lors du déplacement des bielles d’une locomotive à vapeur.
Base (en bleu) et roulante (en vert) du mouvement associé au système bielle-manivelle, dont les bases de glissement sont en mauve.
Un joli cas est aussi celui où les deux courbes C1 et C2 sont identiques. Les glissettes associées sont appelées des courbes de Holditch. Pourquoi donc ? Parce que le dénommé Holditch, révérend de son état, a démontré en 1858 l’étonnant théorème suivant (voir les Surfaces, Bibliothèque Tangente 70, 2020) : si une corde de longueur fixe glisse le long d’une courbe fermée convexe, alors le domaine délimité par la courbe de départ et le lieu géométrique tracé par un point de la corde situé à une distance a d’une extrémité et b de l’autre a pour aire la valeur remarquable πab, indépendante à la fois de la forme et de la longueur de la courbe de départ.
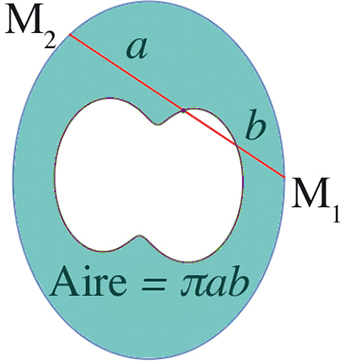
Illustration du théorème de Holditch, dans le cas d’une courbe de glissement elliptique. La non-convexité de la glissette est apparente.
En échangeant calque et feuille
Dans le mouvement dual, les points M1 et M2 sont fixés dans la feuille blanche, et les deux courbes C’1 et C’2 , dessinées sur le calque, sont astreintes à passer par M1 et M2.
Dans le cas où C’1 et C’2 sont deux droites perpendiculaires, il faut imaginer une équerre dont les deux côtés de l’angle droit sont contraints de passer par M1 et M2. Vous connaissez alors certainement le lieu du sommet S de l’équerre !
Les points de la droite (M1S) restent à distance constante de S, donc décrivent une conchoïde du cercle décrit par S, de pôle M1, qui appartient à ce cercle. Il s’agit d’un limaçon de Pascal.
La figure suivante illustre la construction de la base et de la roulante qui sont, comme prévu par dualité, un cercle et un cercle de rayon double, le premier cercle étant précisément celui décrit par S. Cela permet de voir que toutes les glissettes sont des limaçons de Pascal, puisque le point traceur est toujours placé sur un diamètre de la roulante.
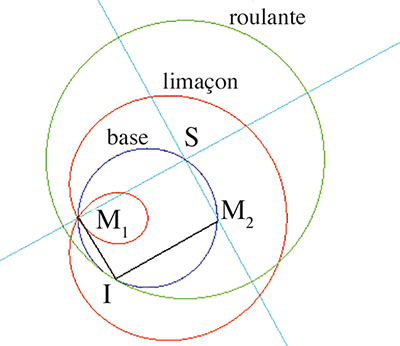
Construction de la base et de la roulante.
Quel est le mouvement où les glissantes consistent en une droite devant passer par M1 et en un cercle de centre Ω devant passer par M2 (cas dual d’une précédente figure) ? Il faut placer une barre double fixée en M2 et articulée en Ω, la deuxième branche passant par M1. Comme prévu, les bases et roulantes (en vert et en bleu) s’échangent, et les glissettes de points qui sont sur la deuxième branche tracent des conchoïdes du cercle, lieu des points Ω.
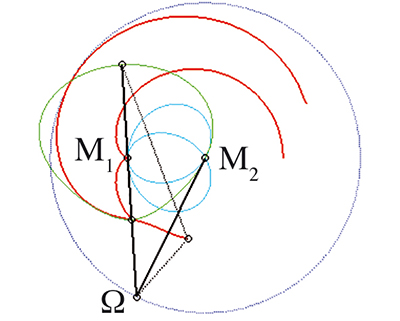
Les glissettes sont des conchoïdes de cercle.
Avec quatre vraies courbes
Et si l’on prenait quatre « vraies » courbes ? L’exemple le plus simple qui vient alors à l’esprit est celui qui fait intervenir quatre cercles. On retrouve le mouvement associé à un trois-barres ! Bien d’autres exemples vous attendent sur l’encyclopédie en ligne des formes mathématiques remarquables, le site Mathcurve, à l’adresse www.mathcurve.com. On le voit, la méthode de génération de mouvements plan sur plan est d’une richesse inépuisable.
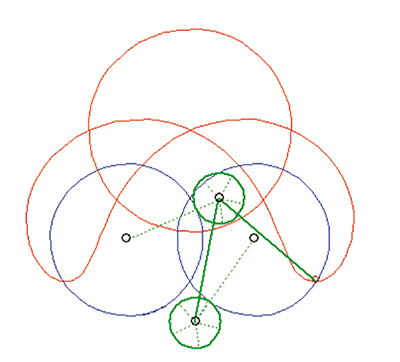
Deux cercles glissent sur deux cercles.
Lire la suite