Des courbes pour dépasser le compas

Les mathématiciens sont très inventifs. Couper un angle en trois, construire un cube de volume double d’un cube donné, trouver un carré de même aire qu’un cercle imposé sont des opérations impossibles à réaliser selon les canons de la géométrie euclidienne, c’est-à-dire avec le seul usage de la règle et du compas, et en un nombre fini de traits de construction.

Le compas, tracés et limites

Entrelacs, arabesques, rosaces et lunules : la géométrie du compas a fait des merveilles en décoration et en architecture. Les maîtres artisans savaient depuis l’Antiquité manier l’instrument, capables qu’ils étaient de tracer, par exemple, au IV ^e siècle avant notre ère, jusqu’à cent quatre-vingt-treize cercles de huit à dix rayons différents pour dessiner la phalère (ornement de bouclier) de bronze de la sépulture à char* de Cuperly, dans la Marne.
(* Dans ces sépultures, on enfouissait les restes du défunt avec son char d’apparat.)

La phalère de Cuperly.

Ils ont su très vite construire des motifs polygonaux réguliers : triangle équilatéral, carré, pentagone, hexagone. Mais ils sont restés arrêtés devant l’heptagone régulier et ses sept côtés récalcitrants, que l’on ne peut effectivement pas construire à la règle et au compas. Une faille dans les innombrables possibilités du compas venait de s’ouvrir : et si d’autres constructions s’avéraient impossibles ? Si tel est le cas, existe-t-il des solutions de remplacement ?

Le mathématicien français Pierre-Laurent Wantzel (1814–1848) a démontré en 1837 qu’il est impossible, à la règle et au compas, de partager un angle en trois angles égaux. Les mathématiciens ont alors, pour le faire malgré tout, exploré diverses pistes : ils y sont arrivés à la règle graduée et au compas, ils ont construit d’ingénieux appareils pour trouver les fameuses trisectrices, comme le compas trisecteur ci-contre, imaginé par Charles Laisant en 1875, où un jeu de losanges croisés permet de définir trois angles de même mesure.

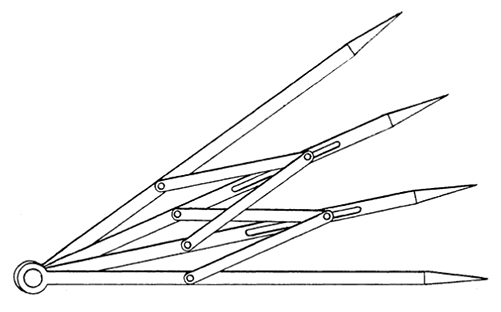
Le trisecteur de Laisant.

Mais qui dispose d’un « compas trisecteur » ? Faute de cet appareil, on peut faire plus simple en utilisant une courbe, et des courbes pour résoudre ce genre de problèmes, les mathématiciens ont été nombreux à en concevoir. L’un des premiers fut le Grec Hippias, qui avait déjà, vers –450, inventé une courbe trisectrice donnant une construction approchée d’un angle tiers d’un angle donné. L’histoire a surtout retenu de cette courbe qu’elle fut, vers –350, réutilisée par Dinostrate pour résoudre… la quadrature du cercle (voir plus loin), et l’a immortalisée sous le nom de quadratrice de Dinostrate. C’est cette même courbe dont s’est inspiré le mathématicien écossais Colin Maclaurin en 1742 pour tracer la trisectrice qui porte désormais son nom.

La trisectrice de Maclaurin.

Définie à partir des points O et A et d’une droite pivotant autour de O, sur laquelle sont alignés O, P et M, la trisectrice de Maclaurin est l’ensemble des points M tels que OP = PA = AM (courbe rouge). Son équation polaire se détermine simplement : avec la loi des sinus dans le triangle OAM, en notant \( \text{OA} = 2a\)  et  \( \theta = \left( \overrightarrow{\text{OA}}, \overrightarrow{\text{OM}} \right)\) , 

on a  \( \dfrac{\text{OA}} {\sin 2\theta} = \dfrac{\text{OM}} {\sin 3\theta} .\)

On obtient  \( \rho= 2a \; \dfrac{\sin 3 \theta} {\sin 2\theta} .\)

Cette courbe en boucle admet O pour point double et passe en particulier par le point S de (OA) tel que OA = 2AS, mais est surtout telle que l’angle  \( \widehat{\text{SAM}}\) soit le triple de l’angle \( \widehat{\text{SOM}}.\)  C’est en ce sens qu’on peut l’utiliser pour « trisecter » un angle : on met en coïncidence son sommet avec le point A, l’un de ses côtés avec la demi-droite [AS), on cherche l’intersection M du second côté de cet angle avec la courbe, on joint ce point à O ; l’angle-tiers recherché est alors  \( \widehat{\text{SOM}}.\)

Des courbes et des machines

Une autre courbe peut être utilisée pour la trisection de l’angle : la conchoïde de Nicomède. Telle qu’elle a été conçue par le mathématicien grec Nicomède au II ^e siècle avant notre ère, cette courbe est une conchoïde de droite, définie, à partir d’une droite δ (en bleu) d’équation x = a dans un repère orthonormé d’origine O et d’un « module »
d = OI, et d’une droite (OM), M décrivant la droite δ.

La conchoïde de Nicomède.

La courbe en question est l’ensemble des points N et P de la droite (OM) tels que ON = OM + d et OP = OM – d. θ étant l’angle polaire du vecteur \( \overrightarrow{\text{OM}}\)  , cette courbe en deux branches a comme équation polaire  \( \rho = \dfrac{a}{\cos \theta} +d.\)

Elle peut aussi être utilisée, avec une configuration semblable à la précédente, comme trisectrice d’un angle  \( \widehat{\text{OIH}}= 3 \alpha.\)

Le cercle de centre I passant par O coupe la courbe en deux points J et K, et (OK) coupe δ en L. Par la définition de cette courbe, KL = KI = OI = d, donc  \( \widehat{\text{KLI}} = \widehat{\text{KIL}}= \alpha\) et, par parallélisme,  \( \widehat{\text{KOQ}}= \alpha.\)

Donc  \( \widehat{\text{OKI}} = \widehat{\text{KOI}}= 2\alpha,\) puis  \( \widehat{\text{IOQ}} = \widehat{\text{OIH}}= 3\alpha.\)

L’angle  \( \widehat{\text{OLH}}\) réalise donc, grâce à la conchoïde, la trisection de l’angle  \( \widehat{\text{OIH}}.\)

Voilà donc quelques exemples de trisection d’un angle. Qu’en est-il de la duplication du cube ? Dupliquer un carré, c’est chose faite depuis que Socrate l’a fait découvrir pas à pas au jeune esclave de Ménon, dans l’œuvre de Platon, vers –402 (voir encadré).

[encadre]

Un extrait du Ménon de Platon

« Est-ce en dessinant un carré au côté double que l’on obtient une surface double ?

– Non, par Zeus !

– Alors, mon garçon, le carré de côté double n’a pas une surface double, mais une surface quadruple. […]

– Mais cette ligne-là, qui va d’un coin de ce carré à l’autre coin, est-ce qu’elle ne coupe pas le carré en deux parties égales ?

– Oui. […] Et ne voilà-t-il pas quatre lignes entourant la surface que voici ?

– Les voilà !

– C’est en partant de la diagonale que l’on construit le carré de surface double !

– Oui, Socrate, c’est évident ! »

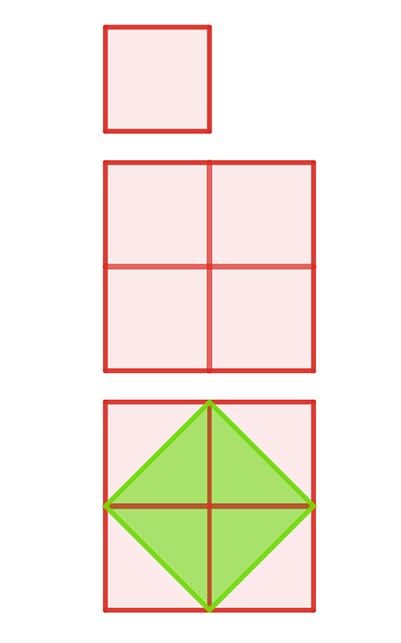
La duplication du carré selon Socrate.

[/encadre]

Mais dupliquer un cube, c’est-à-dire construire en un nombre fini de traits de construction un cube de volume double d’un cube donné ? Le problème se serait posé aux habitants de Délos, victimes d’une épidémie de peste. L’oracle leur aurait recommandé de doubler le volume de l’autel consacré à Apollon. Difficile sans les conseils de Platon, qui sait seulement leur dire de s’intéresser davantage à la géométrie… Et les géomètres, même bien longtemps après, se sont intéressés au problème, sans succès, jusqu’à la démonstration d’impossibilité de Pierre-Laurent Wantzel en 1837. Pas plus que celui de la trisection de l’angle, ce problème, dit le mathématicien français, ne peut être résolu à la règle et au compas. Qu’à cela ne tienne, les mathématiciens, jamais à cours d’imagination, ont inventé des courbes pour approcher le résultat, à savoir, à partir d’une valeur donnée a de l’arête d’un cube, déterminer l’arête x du cube de volume double :  \( x = a \sqrt [3]{2}.\)

Une construction géométrique subtile permet, par l’insertion de deux moyennes proportionnelles x et y entre a et 2a, donc telles que  \( \dfrac{a}{x} = \dfrac{x}{y} = \dfrac{y}{2a}, \) de construire, pour une longueur a donnée, un segment de la longueur voulue,  \( x = a \sqrt [3]{2}.\)

Cette construction peut être facilitée par l’intervention d’une conchoïde de Nicomède de module a, précisément, qui peut donc être considérée comme une courbe « duplicatrice ». À ce procédé un peu délicat, on préférera le tracé d’une autre de ces courbes, la cissoïde de Dioclès. Imaginée par ce mathématicien, au II ^e siècle avant notre ère, décrite dans son ouvrage Sur les miroirs ardents, elle a précisément été conçue comme outil pour dupliquer un cube.

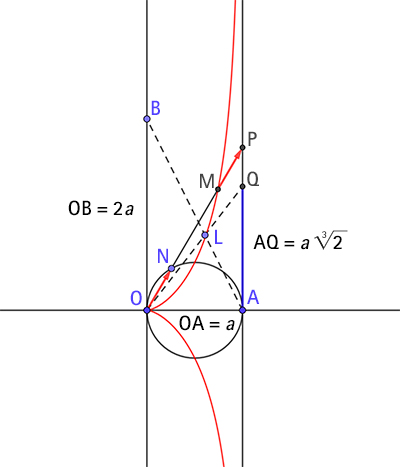
La cissoïde de Dioclès.

Cette courbe est en effet l’ensemble des points M tels que, si la droite (OM) coupe le cercle de diamètre [OA] en N et la perpendiculaire à (OA) passant par A en P, on ait  \( \overrightarrow{\text{ON}} = \overrightarrow{\text{MP}}. \)

En paramétrant, si  \( \theta = \widehat{\left( \overrightarrow{\text{OA}}, \overrightarrow{\text{OP}} \right)},\) avec t = tan θ, les équations de la cissoïde sont :

\( \left \{ \begin{array}{l} x= \dfrac{at^2}{1+t^2}, \\[3mm] y = tx = \dfrac{at^3}{1+t^2}. \end{array} \right.\)  

Elles permettent, si L est l’intersection (tracée en pointillés) de cette fameuse courbe avec la droite (AB), d’équation y = –2x + 2a, si OB = 2a, d’écrire, pour l’ordonnée de L,  \( \dfrac{at^3}{1+t^2} = \dfrac{-2at^2}{1+t^2} +2a, \)  qui donne t ³ = 2.

Ainsi, le point Q, qui a pour abscisse a, aura-t-il pour ordonnée  \( a \sqrt [3]{2}.\)

C’est la longueur AQ qui donnera, par l’intermédiaire de la cissoïde, l’arête du cube de volume double.

 
Quarrer un cercle, l’inaccessible Graal

Troisième des grands problèmes de l’Antiquité irrésolubles par un tracé à la règle et au compas, et non des moindres, voici le problème de la quadrature du cercle. Ce n’est pas pour rien si l’on dit parfois d’une question épineuse : « La résoudre, c’est la quadrature du cercle ! » Il s’agit de construire, règle et compas en main, un carré de même aire qu’un disque donné, par exemple de rayon 1, donc d’aire π. Il suffit (oui !) donc de savoir construire une longueur égale à  \( \sqrt{\pi}.\)  Or, dans le plan euclidien, qui sait construire une longueur égale à π sait aussi construire  \( \sqrt{\pi}.\)  Les mathématiciens s’y sont essayés sans relâche depuis trois millénaires. Finalement, le mathématicien allemand Ferdinand von Lindemann, en prouvant en 1882 la transcendance du nombre π, a mis fin au rêve : inutile d’essayer de « quarrer » le cercle en construisant à la règle et au compas la racine carrée de ce nombre, puisqu’on vous dit qu’il est transcendant ! Qu’à cela ne tienne : nous allons trouver des subterfuges, dit la communauté mathématique.

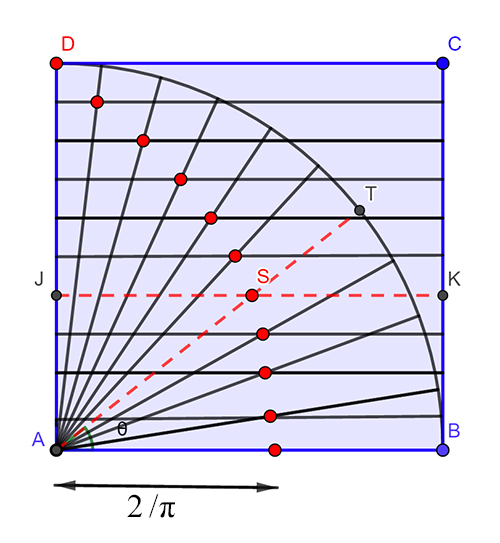
La quadratrice d’Hippias est construite à partir des points rouges.

Découverte par le géomètre grec Hippias d’Élias en –430, puis étudiée par Dinostrate en
–350, la quadratrice, utilisée d’abord pour la trisection de l’angle, peut convenir aussi pour la quadrature du cercle. Cette courbe, qui porte donc aussi bien le nom d’Hippias que celui de Dinostrate, est la trajectoire de l’intersection S entre une droite en translation uniforme (comme la droite (JK)) et une droite en rotation uniforme (comme (AT)). 

Son équation polaire repose sur le fait que, si on désigne par θ l’angle  \( \widehat{\left( \overrightarrow{\text{AB}}, \overrightarrow{\text{AS}} \right)}, \) alors  \( \theta = \dfrac{\pi}{2} y\) si y est l’ordonnée du point courant S (OS = ρ) de la courbe. Ainsi, comme y = ρ sin θ, l’équation cherchée est  \( \rho = \dfrac{2\theta}{\pi \sin \theta}.\)

Cette quadratrice coupe donc l’axe des abscisses au point d’abscisse 2/π… Et voilà apparaître la longueur π fatidique !

Facile, maintenant, avec le théorème de Thalès, de construire une longueur égale à π/2, puis à π, et à partir de là, avec un simple triangle rectangle, une longueur égale à  \( \sqrt{\pi}\)  et enfin un carré d’aire π.

Voilà donc trois grands problèmes de la géométrie classique résolus, certes de manière approchée, mais à l’aide de courbes aussi esthétiques qu’astucieuses, qui ont permis de dépasser la géométrie du compas.