Paraboles et chaînettes

La parabole comme la chaînette sont deux courbes pouvant être observées dans la vie courante. Enfin, en partie seulement, puisqu’elles vont toutes les deux à l’infini.

La première, la parabole, est la vue en perspective d’un cercle à l’intérieur duquel on se trouve (par exemple les gradins d’un théâtre circulaire) ou, dans certains cas, la trace lumineuse que fait un abat-jour ou une lampe de poche sur un mur. On la remarque aussi dans la forme des jets d’eau, ou des trajectoires des fusées des feux d’artifice. C’est enfin la première courbe mathématique que les élèves de seconde tracent lorsqu’on leur fait étudier le graphe de la fonction « (élévation au) carré ».

Le cône de lumière issu d’une lampe de poche correctement orientée vers un mur dessine une parabole.

Un feu d’artifice.

La seconde, la chaînette, est la forme prise par un collier, une chaîne, ou tout fil pesant inextensible suspendu entre deux points.

Ces colliers matérialisent autant de chaînettes.

En 1638, Galilée écrit, dans son Discours concernant deux sciences nouvelles : « On plante sur un mur à une certaine hauteur deux clous […]. À ces deux clous, on suspend une fine chaînette […]. Cette chaînette prend alors une forme de parabole. » Il a aussi consigné ailleurs que la courbe suivie par le fil était « approximativement » un arc de parabole, l’approximation s’améliorant quand on diminue la longueur du fil.

Ce sont Gottfried Wilhelm Leibniz (1646−1716), Jean Bernoulli (1667−1748) et Christian Huygens (1629−1695) qui ont trouvé, indépendamment, en 1691, les équations de la chaînette, qui ne sont pas les mêmes que celles de la parabole.

Deux courbes bien distinctes

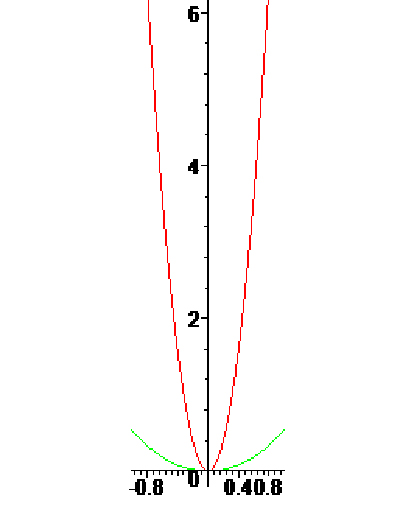
Dans un repère (Oxy), les équations les plus simples de la parabole et de la chaînette sont respectivement y = x ² et y = ch x, où ch (aussi noté cosh sur certaines calculatrices par exemple) est la fonction cosinus hyperbolique. Par définition, ch x = (e ^x + e ^- x )/2.

Une première différence entre les deux courbes, fondamentale pour un algébriste, est que la première est algébrique, et l’autre non. Une courbe est algébrique si l’on peut mettre son équation sous la forme P(x, y) = 0, où P est un polynôme. Pour la parabole, P(x, y) vaut évidemment y – x ², mais, même si ch x peut être développé sous la forme
x + x ²/2 + x ⁴/24 + … + x ²ⁿ/(2n)! + …, cette « somme » possède une infinité de termes, et il n’est pas possible de mettre y – ch x = 0 sous la forme P(x, y) = 0 avec P une fonction polynomiale.

En rouge, la parabole d’équation y = x ², 
en vert, la chaînette d’équation y  = ch x ( sur l’intervalle [ – 1, 1 ] ).

Si l’on fait subir à une courbe d’équation y =  f  (x) une homothétie de centre O et de rapport a, l’équation de la courbe transformée est y = af (x/a). Partant de y = x ², on obtient donc par ce procédé y = x ² /a. Ainsi, une homothétie (ou « élongation dans toutes les directions ») revient à une dilatation suivant l’axe (Oy). Plus généralement, si on désigne par « parabole » l’image par une similitude du plan (une rotation suivie d’une homothétie) de la courbe y = x ², on peut observer que toute transformation affine d’une parabole produit une parabole, ce qui n’est pas le cas pour la chaînette. C’est une deuxième différence entre les deux courbes.

Regardons maintenant plus attentivement la figure précédente. La chaînette semble « plus évasée » que la parabole, mais on constate que cet effet disparaît si l’on trace ces courbes sur un intervalle plus grand.

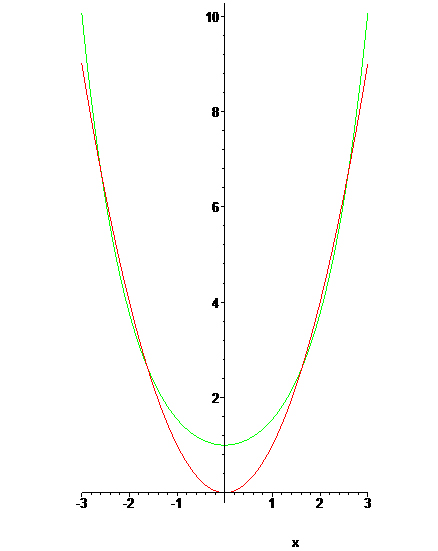
En rouge, la parabole, en vert, la chaînette, sur l’intervalle [ – 3, 3 ].
Les deux courbes semblent coïncider.

Le rendu est encore plus net si l’on modifie la parabole de sorte à avoir la même courbure au sommet. La courbure d’une courbe en un point à tangente horizontale est égale à
f  ′′( x ) ; elle vaut donc, en O(0, 0), 2 pour y = x ² et 1 pour y = ch x. Traçons donc dans un même repère y = x ² /2 et y = ch x – 1 : on a bien la même courbure en O, mais la parabole est ensuite plus évasée.

En rouge, la parabole d’équation y = x 2 / 2.
En vert, la chaînette d’équation y = ch x – 1.

En rouge, la parabole d’équation y = 10 x 2.
En vert, la chaînette d’équation y = ch x – 1.

Multiplions maintenant x ² par un « gros » coefficient (10, par exemple) : la parabole « semble aller beaucoup plus vite vers l’infini ». Mais ce n’est qu’une impression ! L’utilisation d’un logiciel de calcul formel nous permet de savoir qu’à partir de x = 6, 8448… la chaînette repasse au-dessus de la parabole. Ce phénomène se reproduira même si l’on multiplie le coefficient x ² par une constante plus grande que 10. C’est une troisième différence. Cela provient du fait que la quantité ch x – a x ² tend vers l’infini lorsque x croît vers l’infini, provenant lui-même de la propriété classique de croissance comparée entre exponentielle et carré : e ^x/ x ² tend vers l’infini en l’infini.

Deux types de collier

Même si on ne va pas « jusqu’à l’infini », la parabole et la chaînette n’ont pas tout à fait « la même forme ». Dans la figure ci-contre, on a suspendu entre deux points distants de 1 des paraboles de longueurs 1, puis 1,1, 1,5, 2, 3 et 4. On a fait de même avec des chaînettes.

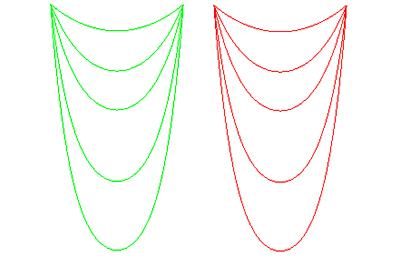
Paraboles et chaînettes de longueurs identiques. Les courbes vertes donnent bien l’idée que l’on se fait de la forme d’un collier de perles !

Comme Galilée l’avait très bien remarqué, au début, on ne voit pas une grande différence. Mais plus on augmente la longueur, plus la parabole devient « pointue ». C’est une quatrième différence entre les deux courbes.

Amusons-nous à calculer la courbure c au sommet des deux courbes en fonction de leur demi-longueur L : on trouve que sh (c)/c = L pour la chaînette, et que   \( \sqrt{c ^2 +1 } +\text{sh}^{-1} (c) / c = \text{L}\) pour la parabole, avec sh (parfois noté sinh) le sinus hyperbolique, à savoir  \( \text{sh} (x) = \dfrac{e^x -e^{-x}}{2}.\)

On en déduit que la courbure c est équivalente à ln L quand L tend vers l’infini pour la chaînette (avec ln le logarithme népérien), et que c est équivalente à L pour la parabole. La courbure au sommet de la parabole croît donc bien plus vite que celle de la chaînette quand la longueur augmente !

La réalisation de ces colliers n’est pas si aisée, du point de vue mathématique, car il faut calculer les longueurs respectives des paraboles et des chaînettes. Les calculs se trouvent en encadré.

[encadre]

Calcul d’une chaînette
ou d’une parabole de longueur donnée

Prenons pour commencer la chaînette d’équation  \( y = f(x) = \dfrac{\text{ch} \, kx -1}{k}, \)  

pour x entre –1 et 1.

La demi-longueur L vaut  \( \int^1_0 \sqrt{1+f'^2(x)} \,dx = \int^1_0 \sqrt{1+\text{sh}^2(kx)} \,dx = \dfrac{\text{sh}\, k}{k}.\)

 La chaînette de longueur 2L a donc pour équation \( y = \dfrac{\text{ch} \, kx -1}{k},\)
k étant défini par l’égalité  \( \dfrac{\text{sh} \, k}{k} = \text{L}.\)

Maintenant, pour la parabole, on prend  \( y = k\, \dfrac{x^2}{2}.\)

La demi-longueur L vaut  \( \int^1_0 \sqrt{1+k^2\,x^2} \,dx = \dfrac{1}{2} \left( \sqrt{1+k^2} + \dfrac{\text{sh}^{-1} k}{k}\right).\)

L’arc de parabole de longueur 2L a donc pour équation   \( \) \( y = k\, \dfrac{x^2}{2},\)

k étant défini par l’égalité  \( \dfrac{1}{2} \left( \sqrt{1+k^2} + \dfrac{\text{sh}^{-1} k}{k}\right) = \text{L}.\)

[/encadre]

Avec un fil élastique…

Supposons maintenant que le fil pesant suspendu soit extensible. Tous calculs faits, la courbe suivie par ce fil, appelée chaînette élastique, a pour paramétrage  \( \left \{ \begin{array}{l} x=au + b \text{sh} \,u, \\[1mm] y= a \text{ch} \, u + \dfrac{b}{2} \text{sh}^2 u, \end{array} \right.\) où b/a est le coefficient d’élasticité. Pour b = 0, on obtient, c’était prévisible, la chaînette ordinaire. Pour a = 0, soit une élasticité « infinie », on retrouve la parabole d’équation x ² = 2by.

Sur la figure suivante sont représentées diverses chaînettes élastiques reliant la chaînette (en haut) et la parabole (en bas). Les deux courbes possèdent donc bien des similarités, comme on pouvait le deviner !

Diverses chaînettes élastiques relient la chaînette (en vert)
et la parabole (en rouge).

La courbe du pont suspendu est la forme prise par le câble supérieur d’un pont suspendu à lui par des tiges verticales.

Tous calculs faits, cette courbe a pour paramétrage   \( \left \{ \begin{array}{l} x= c^2 \int^t_0 \dfrac{\text{ch}\,u}{a+b\text{ch}\,u} \,du, \\[5mm] y= c^2 \int^t_0 \dfrac{\text{sh}\,u \times \text{ch}\,u}{a+b\text{ch}\,u} \,du, \end{array} \right.\)

où les constantes a et b sont, la première, proportionnelle à la masse linéique du tablier du pont supposé rectiligne, et, la seconde, proportionnelle à la masse linéique du câble. Dans les cas habituels, a est « très grand » devant b et l’on prend donc,

concrètement,b = 0 dans les formules, ce qui donne  \( \left \{ \begin{array}{l} x= \dfrac{c ^2}{a}\, \text{sh}\, t, \\[4mm] y= \dfrac{c^2}{2a}\, \text{sh}^2\, t. \end{array} \right.\)

Il s’agit d’une parabole !

À l’autre extrême, si l’on prend a = 0, on obtient  \( \left \{ \begin{array}{l} x= \dfrac{c ^2}{b}\, t, \\[4mm] y= \dfrac{c^2}{b}\, \text{ch}\, t. \end{array} \right.\)

On obtient une chaînette. Voici une nouvelle façon de marier ces deux courbes !

Le pont suspendu à chaînes de Clifton en Grande-Bretagne.