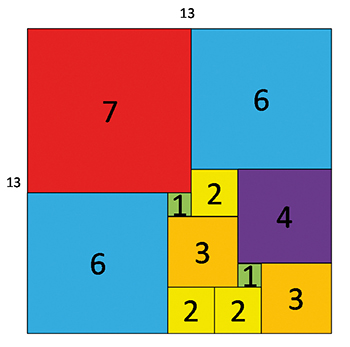
L'Américain Samuel Loyd (1841–1911) était le concurrent de Dudeney. Dans un problème intitulé « Le kilt de Monsieur Perkin », il a proposé le découpage suivant, qui n'est pas parfait car certains entiers sont redondants.

En 1925, le mathématicien polonais Zbigniew Moroń (1904-1971) publie un découpage d'un rectangle (presque carré, avec ses dimensions de 33 par 32) en neuf carrés. De fait, il publie le premier rectangle quarré simple parfait. En 1903, le topologiste Max Dehn (1878-1952), alors élève de Hilbert, avait établi le théorème suivant : un rectangle peut être quarré (composé uniquement de carrés) si, et seulement si, ses côtés sont commensurables. Le rapport des longueurs des côtés doivent ainsi former un nombre rationnel.

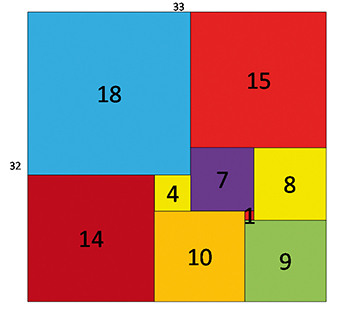
Le plus petit carré parfait

Au Japon, Michio Abe publie en 1930 un article, Covering the square by squares without overlapping, sur le pavage des carrés avec des carrés. Travaillant de manière isolée, il découvre en outre plus de six cents rectangles quarrés simples parfaits ! S'est-il inspiré de sangakus, ces fameuses énigmes géométriques japonaises gravées sur des tablettes votives ?

La même année, le mathématicien russe Maurice Kraitchik (1882–1957) publie une communication de Nikolaï Lusin. Ce dernier affirme (à tort !) qu'il est impossible de découper un carré en un nombre fini de carrés distincts…

En 1938, Roland Percival Sprague (1894-1967) trouve le premier carré quarré simple parfait en utilisant… des rectangles quarré simples parfaits découverts par Moroń (voir ci-contre) !

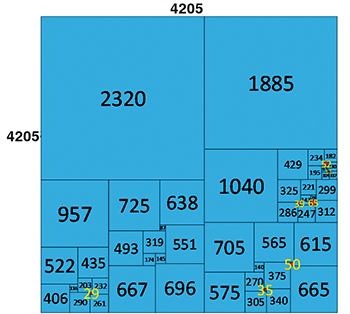
L'informatique s'est ensuite invitée avec A.J.W. Duijvestijn (1927-1998). Avec Christoffel Jacob Bouwkamp (1915–2003), ils établissent que le plus petit carré simple parfait doit être d'ordre au moins égal à 20. Le 22 mars 1978, Duijvestijn trouve le plus petit carré quarré simple parfait d'ordre 21. Il prouvera en outre qu'il n'existe pas de carré simple parfait d'ordre 20.