Un amat(h)eur de dissections géométriques a introduit des méthodes puissantes qui restent aujourd'hui des classiques.

Tout est possible dans l'univers des polygones depuis que le mathématicien allemand David Hilbert (1862-1943) a démontré le théorème suivant : tout polygone peut, après découpage en un nombre fini de parties, être réassemblé en tout autre polygone de même aire.

La démonstration de ce résultat repose sur les deux propriétés suivantes : tout polygone peut être triangulé (c'est-à-dire divisé en un nombre fini de triangles), et tout triangle peut, après découpage, être réassemblé pour former un rectangle de base donnée. Toute la difficulté consiste à être économe dans le nombre des morceaux ! Et l'on n'est jamais absolument certain d'avoir atteint le minimum, puisqu'il est rare qu'on puisse le démontrer… C'est pourquoi ce domaine est encore à la portée des amateurs (au sens noble du terme). Harry Lindgren était de ceux-là.

 

Découpages : un inventaire aussi complet que possible

Dans les années 1950-1960, il produisit un très grand nombre de nouveaux découpages, améliorant plusieurs records de ses prédécesseurs. Il publie en 1964 Geometric Dissections (Van Nostrand) où il fait un inventaire complet de tous les découpages connus, depuis Abu al-Wafa jusque dans les années 1960. De plus, il expose les nouvelles méthodes qu'il a mises au point, permettant de produire des découpages à volonté, bien que parfois des solutions minimales puissent exister en dehors de toute méthode.

  

La méthode des bandes

L'une des méthodes introduites par Harry Lindgren dans le domaine des dissections est la méthodes des bandes. Elle consiste à découper plusieurs exemplaires du polygone à transformer, d'une façon simple, qui permette de former une bande continue à bords parallèles.

 

 

 

 

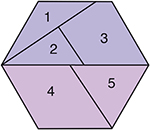
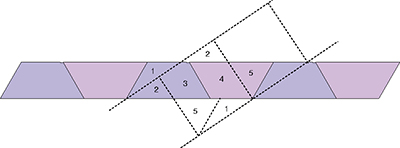
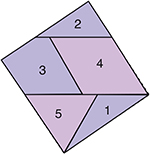Une autre méthode systématiquement utilisée par Harry Lindgren est celle des pavages. En adaptant sa méthode des pavages, on trouve une jolie mosaïque faite de carrés et de triangles équilatéraux superposés, le tout en quatre morceaux différents seulement. Les points congruents sont aux milieux des côtés des carrés et des triangles équilatéraux. On retrouve ainsi les quatre morceaux de la solution Dudeney pour passer du triangle équilatéral au carré !