Si les géomètres grecs, dont Euclide, ont abondamment utilisé des découpages, notamment comme argument de démonstration, le premier ouvrage qui étudie le sujet de façon systématique est celui d'un mathématicien persan : Abu al-Wafa, qui vécut à Bagdad au X^e siècle. Dans un ouvrage intitulé Livre sur les constructions géométriques nécessaires à l'artisan (Kitab al-Handasa), il traite de façon systématique des problèmes de découpage.

Construction : les méthodes des artisans 

L'œuvre scientifique d'al-Wafa aborde aussi bien l'astronomie, l'optique, la trigonométrie (plane et sphérique) ou l'arithmétique que la géométrie. Il s'intéresse notamment aux constructions géométriques et à leur utilité pour le travail des artisans (voir Tangente 139, dossier « Mathématiques arabes »). Ceux-ci utilisaient alors des méthodes qu'ils se transmettaient de génération en génération, dont la plupart étaient seulement approchées. Abu al-Wafa oppose les constructions empiriques (et parfois inexactes) des artisans aux constructions exactes (mais souvent concrètement difficilement applicables) des mathématiciens. Il essaie de poser les bases théoriques de procédés simples réalisables pratiquement par les artisans, en privilégiant les constructions faisables avec un compas d'écartement constant.

C'est ainsi qu'il pose un premier problème : comment réaliser un grand carré à partir de n petits carrés identiques ? Si n est le carré d'un entier, c'est facile. De même, la solution pour n = 2 est immédiate.

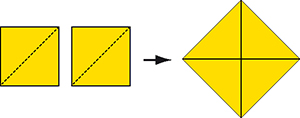
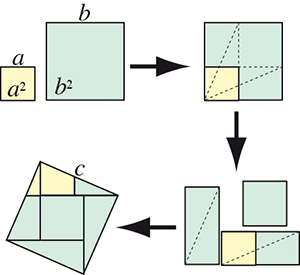
Pour n = 3, la solution suivante, avec six pièces, était connue du temps d'Abu al-Wafa. Malheureusement, elle est seulement approchée ! En effet, si l'on prend le côté d'un petit carré comme unité, l'hypoténuse des triangles rectangles isocèles, a et b, vaut √2, soit environ 1,414, tandis que la juxtaposition du côté du carré vert et de la petite base d'un des deux trapèzes mesure exactement 1,5.

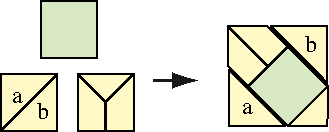
Mais al-Wafa expose une dissection exacte en neuf morceaux. Partons du carré vert. Si, sur chaque côté du carré, on adosse des demi-carrés (jaunes sur la figure), en joignant les sommets des angles droits des demi-carrés, on obtient un grand carré. Pour des raisons de symétrie, les parties qui dépassent du grand carré viennent combler les parties laissées vides. Cette construction demeure valide dans les cas où le carré vert n'a pas la même taille que les carrés jaunes (il est seulement nécessaire que l'hypoténuse des carrés jaunes soit plus longue que le côté du carré vert).

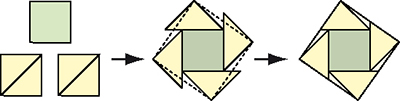
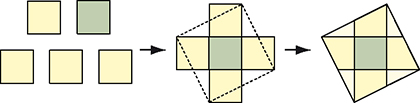
Pour cinq carrés, la solution d'al-Wafa est devenue un grand classique des problèmes de découpages (voir ci-contre).

Le savant persan traite également le cas de deux carrés inégaux. Il propose deux solutions pour reconstituer un grand carré ; la seconde lui sert de support pour démontrer le théorème de Pythagore.

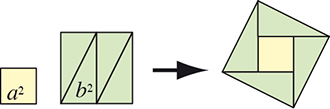
Il met enfin au point une méthode générale permettant de passer de a² + b² carrés identiques à un unique grand carré en utilisant une grille. Par exemple, il passe de dix-sept carrés (a = 1, b = 4) à un seul. Le nombre de pièces est donné par la formule suivante : a² + b² + 2 (a + b – PGCD (a, b)), avec PGCD (a, b) le plus grand commun diviseur à a et b. La formule prévoit dans cet exemple vingt-cinq pièces.

La méthode peut cependant s'avérer difficile à mettre en œuvre pour certaines valeurs de n. En effet, il faut distinguer les cas où n est un carré (cas évident), ou une somme de deux carrés, des cas où il n'est ni l'un ni l'autre. Mais tout nombre entier naturel est somme d'au plus quatre carrés (résultat établi par Joseph-Louis Lagrange en 1770). D'autres mathématiciens, professionnels et amateurs, se sont donc attachés à améliorer ces techniques, et ce jusqu'à nos jours.

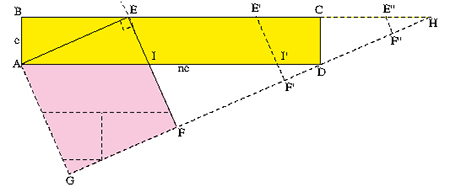
En 1778, Jean-Étienne Montucla ramena la question au problème suivant. On peut toujours disposer n carrés identiques, de côté c, en un rectangle c × nc en les plaçant bout à bout. Il s'agit alors de découper un tel rectangle c × nc en un nombre fini de morceaux qui puissent se réassembler en un carré de côté c√n. Montucla considère le cas plus général où n n'est pas seulement entier, mais un rationnel, voire un réel. Il distingue alors deux cas. Dans le premier cas, on a nc < 2c, donc n < 2. La méthode consiste à placer un point E sur la longueur [BC] du rectangle ABCD de telle sorte que AE soit égal à la moyenne proportionnelle entre c et nc, c'est-à-dire à c√n. Deux perpendiculaires à (AE) menées par A et par E coupent ensuite la parallèle à (AE) passant par D respectivement en G et en F, ce qui achève la construction.

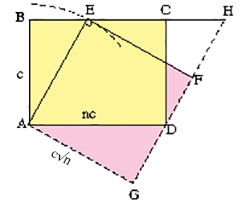
Si nc = 2c (et donc n = 2), on obtient le partage classique des deux petits carrés par une diagonale, chaque moitié d'un petit carré devenant un quart du grand carré.

Le second cas est celui où nc > 2c. La méthode est analogue à celle du premier cas, mais on doit reporter la longueur AI autant de fois que nécessaire sur le côté [BC] et découper autant de parallélogrammes (comme EE'I'I) que le nécessite la longueur de la bande.

Un grand créateur : Henri Dudeney 

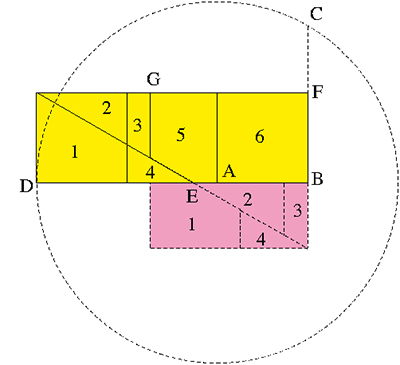
Former un grand carré avec trois carrés identiques : la solution de Dudeney (le cercle de centre A a pour rayon AD, et on a BC = DE = EF). 

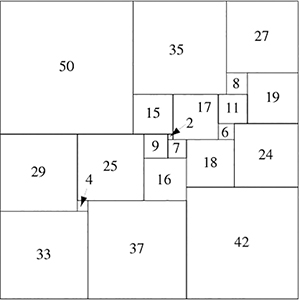
Ces différents découpages peuvent dans certains cas être considérés comme des puzzles. Une catégorie particulièrement élégante est celle des rectangles ou des carrés dits parfaits. Ce sont des rectangles (ou des carrés) constitués de carrés tous différents. Pendant longtemps, on a supposé qu'il était impossible de trouver un carré parfait (voir Drôles de carrelages, dans Tangente 3). Le plus petit carré parfait ne fut débusqué qu'en 1978 par Adriannus Johannes Wilhelmus Duijvestijn ; il est d'ordre 21 et de côté 112.

Dudeney, qui a créé des centaines de récréations mathématiques originales, est resté célèbre pour un autre découpage : celui d'un triangle équilatéral en quatre pièces permettant de former un carré. Le ludologue était si fier de son invention qu'il la présenta à Londres en 1905 devant la Royal Society.

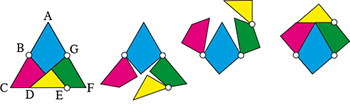
Le puzzle de Dudeney.

Le caractère extraordinaire du puzzle de Dudeney est triple. Déjà, il met en jeu les deux figures les plus simples et les plus connues de la géométrie plane. Il est en outre constitué de quatre morceaux seulement. Enfin, et surtout, il est possible d'articuler entre elles les quatre pièces et de passer de la configuration en triangle à la configuration en carré en faisant simplement jouer les articulations entre les pièces. Celles-ci forment une chaîne articulée qui peut se refermer dans un sens pour former un triangle, et dans l'autre pour former un carré.

Dans la construction de ce puzzle, si les points B et G sont bien les milieux respectifs des côtés [AC] et [AF], contrairement peut-être aux apparences, les points D et E ne sont pas situés au quart et aux trois quarts de [CF]. On aurait alors seulement une construction approchée, qui ne fournirait pas exactement un carré, mais un rectangle. La construction exacte de Dudeney est la suivante.

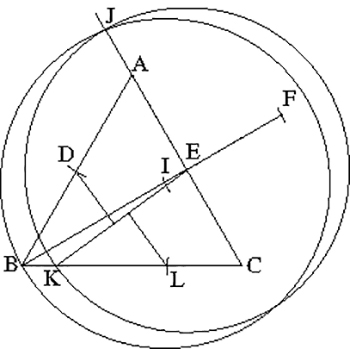
La construction de Dudeney.

On prolonge [BE] du côté de E d'une longueur égale à un demi-côté du triangle. On marque ensuite le point I milieu de [BF], on prolonge [EA] du côté de A, puis on détermine sur cette demi-droite le point J tel que IJ = BI. On trace un arc de cercle de centre E et de rayon EJ, qui coupe BC en K. On reporte ensuite KL, égal au demi-côté du triangle ABC. Il reste à abaisser les perpendiculaires de D et de L sur EK. Le tour est joué !