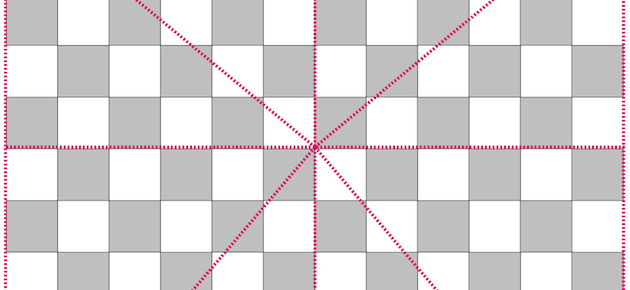
Les jeux de dissection géométrique, qu'ils soient réalisés en bois, en mousse ou en utilisant du carton fort, peuvent être des alliés précieux pour l'enseignant. Leur caractéristique est en effet leur contre-intuitivité. Les élèves comme les amateurs de mathématiques récréatives apprécient tout particulièrement ces découpages qui se révèlent trompeusement simples ou qui présentent très peu de pièces, ce qui donne l'illusion qu'ils peuvent être facilement résolus. Cette simplicité apparente met en évidence, lors de la résolution, certains blocages mentaux ou conditionnements. L'objectif des créateurs de casse-tête est de créer une « disjonction » dans l'esprit du joueur, une « violation de l'attente », qui le stimulera, l'encouragera à penser sans idées préconçues, et sortir des sentiers battus.

Les faux jumeaux

Bien que les deux casse-têtes ci-dessous forment chacun, au début du jeu, un carré de mêmes dimensions avec un trou identique, la petite différence d'angle dans la coupe des pièces est suffisante pour créer des surprises... En observant bien les pièces du premier puzzle (schéma orange), on constate qu'elles ne sont pas irrégulières, comme on pourrait le penser, car l'une de leurs diagonales est en fait un axe de symétrie.

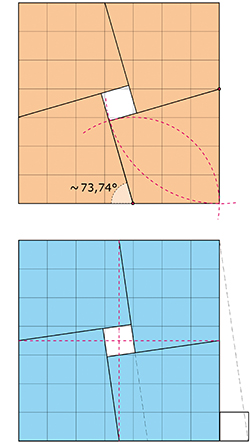
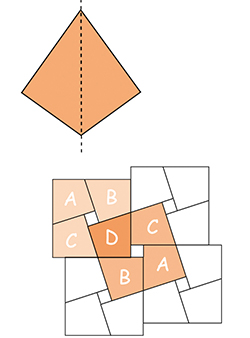
Ceci implique qu'elles ont deux paires de côtés adjacents égaux, comme illustré ci-après, et donc que l'on peut permuter ou tourner ces pièces comme on voudra : elles formeront toujours le même carré initial avec le trou (le pavage présenté sous le quadrilatère doit vous aider à comprendre).

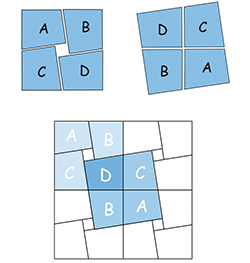
Avec le second puzzle (schéma bleu), on pourra réaliser, en permutant ses pièces, un carré avec ou sans trou, comme démontré ci-dessous. Avec ces deux jeux, nous pouvons réaliser un méchant mais innocent tour à un ami : donnons-lui le premier puzzle et réservons-nous le second. Prions-le de répéter nos gestes et, avec des mouvements rapides et sûrs, réalisons devant ses yeux d'abord le carré du second puzzle (avec un trou, donc), puis, un carré sans trou. Notre pauvre ami quant à lui s'acharnera sur ses pièces, les tournera et les retournera sans résultat. Il n'arrivera jamais à combler ce damné trou.

Toutefois, il existe une méthode (laborieuse) pour faire disparaître ce trou : il suffit de découper le puzzle et de le réassembler comme suit :

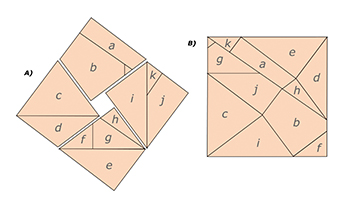
Dissections avec disparition de surface

Voici une variante très ingénieuse de puzzles de disparition géométrique. Reproduisez les modèles ci-dessous sur du bristol ou du carton fort et découpez les huit pièces du jeu.

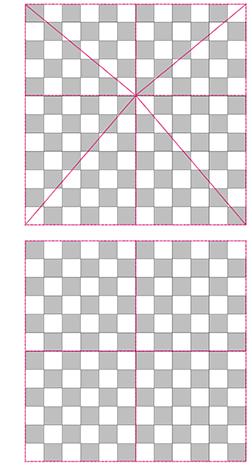
Ce qui semble étrange, c'est qu'il est possible d'arranger ces pièces de deux façons différentes, comme ci-après, sans que la surface du jeu ne soit, apparemment, modifiée. Mais alors, où a disparu l'espace carré manquant ? Le puzzle carré semble conserver ses dimensions, bien qu'il ait une pièce en moins.

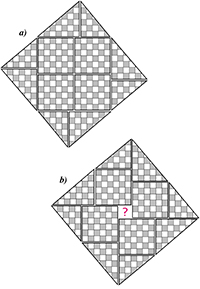
Toutefois, les pièces réunies ne forment jamais un carré parfait : au début, elles forment un octogone légèrement concave (ce qui est difficile apercevoir à l'œil nu), puis un octogone convexe.

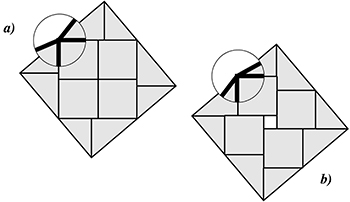
À gauche, le « carré » est en fait un octogone concave ; à droite, c'est un octogone convexe !

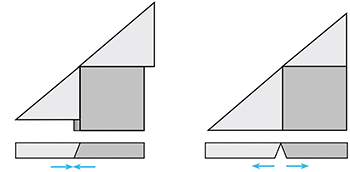
On peut améliorer l'effet de surprise en atténuant le jeu entre les pièces et donc l'effet convexe–concave. Il faudra alors construire le puzzle avec une certaine épaisseur, puis découper les pièces carrées légèrement en biais, comme le suggère la dernière figure. Ainsi, en les retournant d'une certaines façon, elles prendront moins de place (à gauche) ou d'avantage de place (à droite), tout cela à l'insu du spectateur...

Un exemple en vidéo

Dans cette vidéo, vous pourrez observer, en mouvement, une aire qui disparaît.