Les mathématiques sont en grande partie nées de problèmes de partage de récoltes ou de champs. Les géomètres se sont très vite emparés de la division des terres pour en faire les premiers problèmes de découpage, plus de deux mille ans avant notre ère. À l'origine, le sujet est donc très concret ! 

Le Moyen Âge et la Renaissance ont vu naître de véritables méthodes de démonstration fondées sur la décomposition–recomposition de figures.

Enfin, avec le développement de la presse à partir du xix^e siècle, de nombreux problèmes de puzzles et de découpages ont fleuri dans les journaux, répandant dans le grand public cette si ludique « géométrie des ciseaux », volontairement limitée ici aux figures planes à bords rectilignes.

La loi du partage

C'est une toute petite tablette, au numéro barbare de IM 58 045, mais ô combien précieuse ! Elle représente l'équipartition d'un trapèze de bases 7 et 17 coudées, mais sans le résultat. La solution, il faut la chercher sur une autre tablette, YBC 4 675, où le scribe donne cette fois le détail du calcul : la « ligne médiane » mesure 13 coudées. Déjà un problème de découpage, écrit vers – 2 300, époque où les mathématiques étaient surtout utilitaires !

Équipartition du trapèze chez les Babyloniens du III^e millénaire avant notre ère.

Ce bel exemple montre que les scribes de Babylone savaient déjà que l'aire d'un trapèze T ne dépend que de ses bases a et b et de sa hauteur. Il illustre en outre que partager T en deux trapèzes d'aires égales par une « ligne médiane » de longueur t parallèle aux bases se fait en introduisant la quantité  \( t^2=\frac{a^2+b^2}{2}\)  où t est, dit en termes d'aujourd'hui, la moyenne quadratique des deux bases. L'idée a fait son chemin puisqu'on, trouve, vers – 1 500, une autre tablette babylonienne, AO 17 264, relatant le problème des six frères, qui étend cette partition du trapèze à un partage entre six frères, où les deux premiers d'une part, le troisième et le quatrième ensuite, le cinquième et le sixième enfin, devront avoir des parts égales. Le résultat sort de l'ordinaire : en effet, si le « front », ou la base supérieure, fait 3,33 (dans la numération sexagésimale et de juxtaposition des Babyloniens, 3,33 signifie 3 × 60 + 33, soit 213 coudées), le « front » inférieur en fait 51, le côté supérieur 2,15 (soit 135), le côté inférieur 1,21 (soit 81 coudées). Le scribe s'est arrangé, parmi toutes les solutions possibles de segments parallèles aux bases réalisant le partage, pour que leur longueur soit successivement de 183, 147, 123, 93 et 75 coudées. Du grand art !

De nombreux mathématiciens, trop tentés par l'aventure, ont poursuivi dans la voie des dissections de figures. Thabit ibn Qurra (826-901) est l'un d'eux. Dans son traité Sur la preuve attribuée à Socrate sur le carré et ses diagonales, il donne une dissection en cinq morceaux de deux carrés juxtaposés transformés en un seul. Le découpage a priori mystérieux peut être facilement « démonté », selon Paul Mahlo (1908), grâce à  deux réseaux superposés de pavages, l'un fait de grands et de petits carrés, en beige, l'autre, en rouge, fait de carrés identiques.

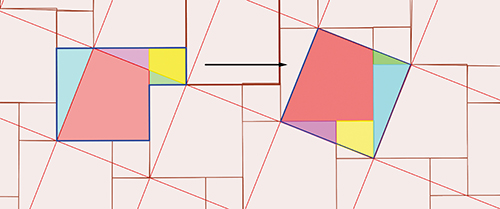
Le puzzle de Thabit ibn Qurra.

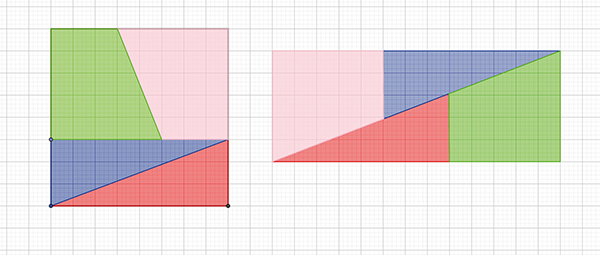
Les deux figures colorées parlent d'elles-mêmes. Si les deux carrés de départ, au lieu d'être de taille différente, sont de même taille, on peut toujours les découper selon une de leurs diagonales pour faire des quatre morceaux obtenus un carré d'aire double : Platon ne fait rien d'autre lorsqu'il relate comment Socrate aide Ménon à comprendre que le carré construit sur la diagonale d'un premier carré double son aire.

Autre mathématicien arabe du X^e siècle, Abu al-Wafa, dans un esprit très didactique, présente dans son Livre sur ce qui est nécessaire à l'artisan en constructions géométriques de nombreux puzzles basés sur des propriétés exclusivement géométriques, sans aucun calcul. Il explique ainsi comment, de trois carrés égaux, n'en faire qu'un seul. 

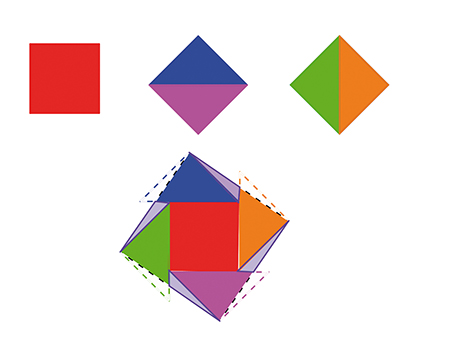
 Abu al-Wafa : trois carrés pour un.

Nous voilà maintenant au cœur du problème : le jeu « décomposition–recomposition » va permettre de prouver, presque par un simple regard, certaines propriétés géométriques.

Découper pour démontrer 

Bien avant Thabit ibn Qurra, Archimède aurait déjà créé le Stomachion, ce puzzle de quatorze pièces qu'on peut réassembler de dix-sept mille cent cinquante-deux façons différentes en un carré, presque un jeu d'enfant ! Mais, disait Montaigne, « les jeux des enfants ne sont pas des jeux et il les faut juger en eux comme leurs plus sérieuses actions », et les dissections de figures géométriques vont vite sortir du domaine du jeu pour investir celui de la preuve.

Le puzzle de Thabit ibn Qurra (voir au-dessus) pour transformer deux carrés de côtés a et b en un seul de côté c peut aussi servir à donner une preuve visuelle du théorème de Pythagore. 

D'autres mathématiciens ont aussi « fait du Pythagore » avant Pythagore, rivalisant d'imagination pour en donner des « preuves sans mots ». Les Chinois par exemple, rompus à la fragmentation de figures, mettent à profit cet art pour en faire des démonstrations reposant sur le principe d'invariance des aires. Ici, tout mathématicien doit savoir manipuler des pièces, c'est-à-dire les découper, les déplacer, éventuellement les retourner, les assembler en comblant au besoin des trous. C'est ce que nous invite à faire cette « figure de l'hypoténuse » dans Zhoubi suanjing (« Canon des calculs gnomoniques des Zhou », dynastie ayant régné sur la Chine environ du XI^e au III^e siècle avant notre ère). Le commentaire stipule que « le carré de l'hypoténuse contient quatre surfaces rouges et une surface jaune », soit, en d'autres termes, c² = 4 (ab / 2) + (b – a)² , qui donne exactement c² = a² + b² : ce découpage ne vaut-il pas démonstration ?

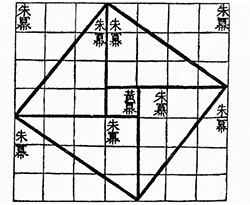
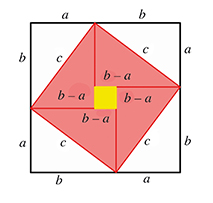
La figure de l'hypoténuse et sa traduction.

On doit à Liu Hui, autre mathématicien chinois, du III^e siècle de notre ère, dans ses Neuf chapitres sur l'art mathématique une preuve par découpage du calcul de l'aire S d'un triangle rectangle de côtés de l'angle droit a et b et d'hypoténuse c en fonction du rayon r de son cercle inscrit et de son demi-périmètre p : S = pr. Ici aussi, la figure parle d'elle-même. 

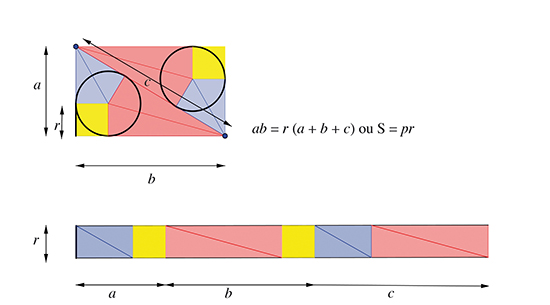
Aire d'un triangle selon Liu Hui.

Ce découpage permet, cette fois encore, de démontrer la formule attendue, mais dans ce domaine, attention aux contrefaçons ! Il existe des découpages approximatifs, comme celui qui permet d'évaluer l'aire d'un cercle.

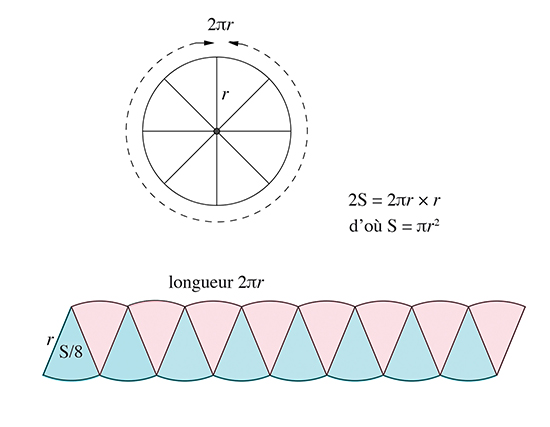
 Aire d'un cercle par découpage.
 

Il existe aussi des découpages « pousse-au-crime », comme celui, célèbre, de Lewis Carroll où un carré de côté 8 décomposé donne naissance à une illusion de rectangle de côtés 5 et 13 et peut amener les imprudents à conclure « 64 = 65 » en comparant les aires. Il s'agit de ne pas rester sur la première impression, mais de faire découpage et assemblage en toute rigueur. Tel est le secret de la réussite d'une démonstration à coups de ciseaux.

L'âge d'or du découpage

À partir du XVIII^e siècle, de nombreux livres de récréations mathématiques contenant des puzzles géométriques fleurissent. Citons les Récréations mathématiques et physiques de Jacques Ozanam (1640-1718), parues en 1778, où il s'agit par exemple, « avec cinq carrés égaux, d'en former un seul », ou d'autres Récréations mathématiques, celles d'Édouard Lucas (1842-1891), qui propose, lui, de « découper un carré en sept parties de manière qu'étant convenablement assemblées elles constituent séparément trois carrés ». Dans ses Curiosités géométriques en 1907, Émile Fourrey résout des problèmes numériques par la géométrie en recollant les morceaux d'un puzzle. N'oublions pas non plus Sam Loyd (1841-1911), qui fait du jeu de Tangram, né en 1848, l'un des jeux géométriques les plus populaires, proposant plusieurs centaines de figures à réaliser avec les sept pièces de ce puzzle… dont certaines impossibles !

L'intérêt pour les dissections géométriques va croissant chez nombre de mathématiciens, dont trois vont démontrer, entre 1807 et 1835, le théorème fondamental affirmant que, si deux polygones ont même aire, l'un peut toujours être découpé en un nombre fini de polygones qui peuvent être réarrangés pour former l'autre. Ci-contre, le puzzle de Henry Dudeney (1857-1930) en donne un magnifique exemple.

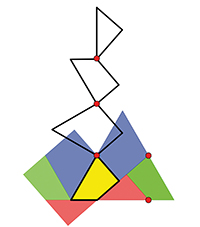
Le puzzle articulé de Dudeney.

Le concepteur de ce puzzle, spécialiste britannique de découpages et casse-tête, a su transformer, en le divisant en quatre morceaux, un triangle équilatéral en carré. Il en a même fait une maquette en bois précieux, avec charnières en cuivre, qu'il a présentée en 1905 à la Royal Society et, fait, remarquable, ce modèle fait partie des puzzles articulés (en anglais, hinged puzzles), catégorie spécialement prisée des amateurs.

Dès la fin du XIX^e siècle, les collections de cartes publicitaires en forme de puzzles faisaient fureur et l'idée même de puzzle s'est répandue dans le grand public. Les journaux contribuent à cet essor, ouvrant leurs colonnes aux puzzles de Sam Loyd et de Henry Dudeney, qui ont d'ailleurs collaboré au même moment à la revue anglaise Tit-Bits. Loyd n'avait pas son pareil pour donner aux puzzles des contextes ludiques et drôles, comme celui de la chaise à porteurs, où il demandait simplement : « Comment fermer la chaise à porteurs ? »

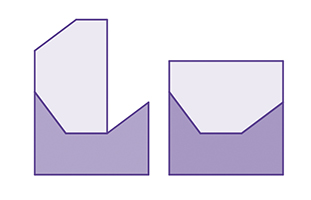
Le puzzle de la chaise à porteurs.

 Amateurs comme professionnels de la géométrie, tous ont, à partir de là, rivalisé d'astuce pour proposer des puzzles de plus en plus sophistiqués. L'un des champions de ces constructions  très imaginatives a été Henry Perigal (1801-1898), agent de change londonien, mathématicien à ses heures, dont le coup d'éclat a été de démontrer par une dissection originale le théorème de Pythagore. La gravure figure même sur l'une des faces de son tombeau à Wennington (Essex). 

La gravure décryptée du tombeau de Perigal.

Un autre de ces champions a été Harry Lindgren (1912-1992), britannique lui aussi, émigré en Australie, géomètre amateur. Spécialiste reconnu de dissections, il en fait un livre, Geometric Dissections (1964). Il savait mieux que quiconque transformer les figures en les replaçant, soit selon des bandes, soit sur un quadrillage. 

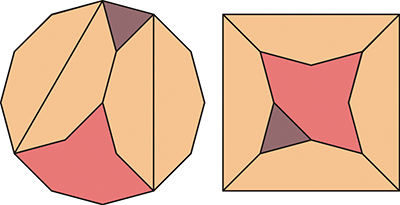
 Dodécagone en carré, dissection de Lindgren.

Mais les dissections ne seraient pas vraiment ce qu'elles sont sans Greg Frederickson, qui a su dans ses riches ouvrages les répertorier, les décrire avec minutie, placer chacune d'elles dans son contexte historique et mathématique, pour nous les faire connaître et nous les faire aimer.