Prenez vos deux polygones préférés, P₁ et P₂, comme l'hexagone régulier et le carré. Une condition nécessaire pour que P₁ et P₂ acceptent la même décomposition polygonale (ils sont alors dits équidécomposables) est, bien évidemment, qu'ils aient la même aire (ils sont alors dits équivalents).

On se convainc aisément que le fait, pour P₁ et P₂, d'être « équivalents » définit bien, au sens technique du terme, une relation d'équivalence sur l'ensemble des polygones. Une relation d'équivalence satisfait en effet trois propriétés : la réflexivité (P₁ a bien la même aire que lui-même), la symétrie (si P₁ a la même aire que P₂, alors P₂ a la même aire que P₁) et la transitivité (si P₁ et P₂ ont même aire et si P₂ et P₃ ont même aire, alors P₁ et P₃ ont aussi la même aire).

Une paternité partagée 

Vérifier la justesse d'une équidécomposition nécessite implicitement le déplacement des pièces constituant le premier polygone pour former le second. Ces déplacements sont des opérations caractéristiques d'une géométrie. Ainsi, notre géométrie euclidienne repose sur le groupe des similitudes, composé de translations, homothéties et rotations. Puisque les pièces déplacées sont invariantes, on se restreint au groupe des isométries, composé des translations et rotations. Les symétries axiales, bien qu'étant des isométries, n'en font pas partie car elles nécessitent un retournement, c'est-à-dire de passer dans la troisième dimension (en sortant du plan).

Une première démonstration

Deux polygones équidécomposables sont donc équivalents, et un théorème prouve la réciproque : deux polygones équivalents sont équidécomposables. Ce théorème est attribué à plusieurs auteurs. Il est le plus fréquemment appelé théorème de Bolyai, mais aussi théorème de Bolyai-Gerwien, de Wallace-Bolyai-Gerwien et même de Lowry-Wallace-Bolyai-Gerwien. Il semble que Farkas Bolyai (1775-1856), le père de János Bolyai (1802-1860, voir Tangente 111), ait le premier posé le problème en 1790, qui aurait été démontré par John Lowry (1769-1850) en 1814. William Wallace (1768-1843) en a retrouvé une preuve en 1831, suivi en 1833 par Bolyai et par le lieutenant prussien (et mathématicien amateur) Paul Gerwien. Mais on ne trouve facilement des publications que des deux derniers.

Les idées nouvelles germent un peu partout quand elles sont mûres. Boileau disait : « Une idée neuve : c'est au contraire une pensée qui a dû venir à tout le monde, et que quelqu'un s'avise le premier d'exprimer. » C'était bien l'opinion de Farkas Bolyai quand il pressait son fils de publier au plus vite ses idées sur la géométrie non euclidienne : « Quand le temps est mûr pour certaines choses, celles-ci apparaissent en divers endroits un peu comme des violettes qui éclosent au début du printemps. » Les faits lui ont donné raison.

Deux voies de démonstration du résultat sont possibles. En s'inspirant de la méthode de Bolyai, il s'agit de montrer que tout polygone est équidécomposable en un carré équivalent. Il suffit alors de superposer, dans ce carré, les décompositions de deux polygones équivalents pour obtenir directement la décomposition entre les deux polygones.

Dans une première étape, tous les polygones sont triangulables, même d'une infinité de façons. Chaque triangle peut ensuite être décomposé en un rectangle de dimensions la base et la demi-hauteur du triangle.

Équidécomposition triangle-rectangle.

Il s'agit ensuite de carrer le rectangle. Tout triangle est donc équidécomposable avec son carré de référence de même surface.

Équidécomposition rectangle-carré.

Un polygone étant un ensemble de triangles, il faut maintenant pouvoir « additionner » les décompositions de deux carrés. De nombreuses démonstrations géométriques de Pythagore peuvent être sollicitées, comme ci-dessous.

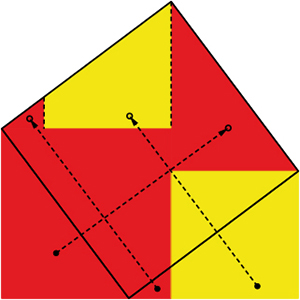
Réduction de deux carrés en un carré.

L'objectif est atteint. Découpons le polygone initial en plusieurs triangles, dont on établit une décomposition permettant de construire un carré. Deux à deux, couplons les décompositions de carrés pour obtenir le puzzle d'un carré plus grand, et ainsi de suite jusqu'à obtenir, au prix de nombreuses découpes théoriques, un carré dont la découpe permet de reconstruire le polygone initial. Puis, par superposition de découpages, deux polygones équivalents quelconques sont équidécomposables.

La démonstration de Gerwien (revisitée)

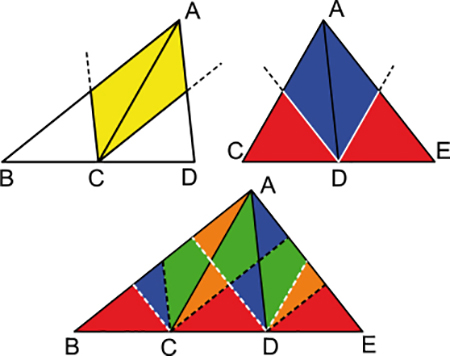
Transitivité de l'équidécomposabilité.

Après avoir amélioré quelques points techniques, voici maintenant la démonstration de Gerwien. On considère tout d'abord deux triangles ACB et ACD, de sommet commun A, et de bases [BC] et [CD] situées sur un axe commun et de même longueur. Le côté commun [AC] est donc la médiane du triangle ABD. Il suffit alors, pour chaque triangle, de mener du sommet C la parallèle au côté opposé. Chaque triangle est alors constitué des deux mêmes triangles (en forme). Sur la même figure, un découpage similaire a été effectué pour les triangles ADC et ADE. Par transitivité, les triangles ABC et ADE sont équidécomposables en quatre parties.

Considérons maintenant des triangles ayant toujours la même hauteur et des bases alignées et de même longueur. Ces triangles sont alors équivalents, puisque leur surface est le demi-produit de la base par la hauteur.

Deux cas de figures se présentent. Si les bases [BC] et [CE] peuvent être jointives en C sans que les triangles se superposent, on prolonge les côtés [AB] et [DE] jusqu'à leur intersection en F. Le segment [FC], médiane du triangle BFE, coupe le segment [AD], parallèle à la ligne de base (BCE), en G, qui est donc, d'après le théorème de Thalès, milieu du segment [AD]. On en déduit que les points A et D sont à la même distance de la médiane [FC], et donc que les triangles AFC et DFC ont la même hauteur. 

Le premier cas.

On met ainsi en évidence deux couples de triangles, à savoir (FCB, FCE) et (FCA, FCD), de même base et même hauteur, donc équidécomposables d'après ce qui précède. En superposant les décompositions, méthode illustrée plus loin, on obtient, par soustraction des éléments constituant les triangles FCA et FCD, la réalisation d'une équidécomposition des triangles ABC et DCE. 

Dans le cas où, en rapprochant les triangles, les sommets se rencontrent avant les bases, on symétrise le problème en ajoutant le milieu F du segment [DE]. De même que précédemment, nous obtenons deux couples de triangles, à savoir (AFB, AFC) et (AFD, AFE), auxquels on peut appliquer la décomposition précédente, pour obtenir l'équidécomposition cherchée, toujours par soustraction. 

Le second cas.
 

Dans ce cas de figure plus simple, est illustrée la superposition des décompositions qui permet d'enlever à la décomposition globale une décomposition partielle. Des croix indiquent d'autre part les éléments à translater et un rond ceux qui subissent une symétrie centrale (et une translation). 

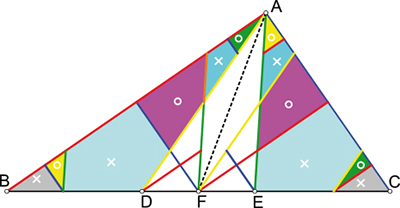
Équidécomposition par soustraction.
 

Considérons deux triangles équivalents quelconques, ABC et CDE. Si [AB] est le plus grand des six côtés, la hauteur associée est la plus petite des six hauteurs, puisque le produit de la hauteur par la base est constant. Les hauteurs du triangle CDE, et donc au moins l'un de ses côtés, sont plus grandes que cette hauteur, ce qui permet la construction suivante. On fait tourner le triangle CDE autour de son sommet C commun avec le triangle ABC jusqu'à ce que le sommet E soit à la même hauteur que le sommet A par rapport à la base [BC]. On déplace ensuite le sommet D parallèlement au côté opposé [CE] jusqu'à ce qu'il se positionne sur la ligne de base, en F. Par construction, les triangles CED et CEF, même base, même hauteur, sont équidécomposables. Le triangle CEF est alors équivalent au triangle ABC avec la même hauteur, d'où BC = CF, ce qui implique, pour les mêmes raisons, son équidécomposabilité avec ABC. Par transitivité, les triangles ABC et CED sont donc équidécomposables.

Équivalence de triangles de même aire.

Il reste à translater le sommet d'un polygone parallèlement à sa corde pour passer d'un n-polygone à un (n – 1)-polygone tout en respectant l'équidécomposabilité. En n – 3 telles opérations, le polygone est transformé en un triangle, ce qui finit de démontrer que deux polygones de même surface sont équidécomposables.

Équivalence d'un n-polygone et d'un (n – 1)-polygone.

Ce processus de construction de découpages, s'il permet d'en démontrer l'existence, n'est pas le plus économique en nombre de pièces. Bien qu'il existe des algorithmes de construction de dissections, aucun n'est capable, pour une découpe de deux formes polygonales données, de déterminer le nombre minimal de pièces. La créativité humaine dans ce domaine n'est pas encore mise en pièces !