De 1957 à 1980, Martin Gardner (1914-2010) a tenu la rubrique de jeux mathématiques du Scientific American (dont la version française est Pour La Science). Il a proposé un problème de découpage de triangle, qui correspond bien à son goût des énigmes d'allures compliquées mais qu'une idée astucieuse rend lumineuses : un triangle obtusangle (ayant un angle obtus) peut-il être découpé en un nombre fini de triangles acutangles (dont tous les angles sont aigus) ? La réponse est oui, en sept triangles plus précisément.

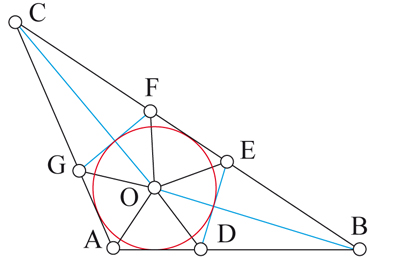
Ces angles sont tous aigus ! De plus, on ne peut faire mieux que sept car l'angle obtus en A doit être coupé par le côté d'un des triangles, qui ne peut se terminer sur le côté [BC], sinon on retrouverait un angle obtus que l'on devrait à nouveau couper… et ainsi de suite. On s'arrête donc en un point à l'intérieur du triangle. En ce point, cinq côtés au moins se rejoignent pour que les angles soient aigus. Cela donne le pentagone à l'intérieur du triangle, donc sept triangles.