
Souvenir de première : l’équation du second degré possède deux solutions réelles, éventuellement confondues, si son discriminant est positif ou nul. Mais, à la lecture de l’énoncé d’un problème, il n’est pas toujours facile de détecter le polynôme du second degré qui fournira la solution à la question posée.
Voici une petite énigme issue de la vie quotidienne. Régine et Christophe ensemble font le ménage de leur petit appartement en trente-six minutes. Plus soigneuse, Régine seule met une demi-heure de plus que Christophe seul. Combien de temps met-elle ?
Appelons t la durée demandée en minutes, R et C les « vitesses » respectives de nos deux compères ; on obtient 36(R + C) = (t – 30)C, égalité qui s’écrit aussi 36(R/C + 1) = (t – 30).
Par ailleurs, t R = (t – 30)C donne R/C = (1 – 30/t). On en déduit 36(2 – 30/t) = (t – 30), soit
t 2 – 102 t + 1 080 = 0, qui admet deux solutions, 12 et 90. Comme t est supérieur à 30, Régine seule met une heure et demie (t = 90) pour faire le ménage de l’appartement.
Cercle inscrit et cercle circonscrit
La géométrie elle aussi fait bon ménage avec l’algèbre. Selon la notation usuelle, soient respectivement r et R le rayon du cercle inscrit et le rayon du cercle circonscrit à un triangle T, a, b et c les longueurs des côtés de T, et p le demi-périmètre de T (de sorte que 2p = a + b + c). Notons enfin S l’aire du triangle. De manière évidente, on a R ≥ r. Peut-on obtenir une inégalité plus précise ?
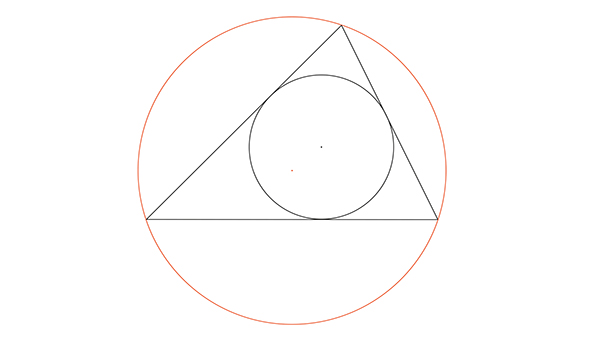
Cercle inscrit dans le triangle (en noir) et cercle circonscrit (en rouge).
Utilisons la transformation de Ravi en effectuant le changement de variables a = y + z, b = z + x et c = x + y, ce qui revient à poser x = (b + c – a)/2, y = (c + a – b)/2 et z = (a + b – c)/2. En raison des inégalités triangulaires dans le triangle (à savoir b + c ≥ a, a + b ≥ c et a + c ≥ b), les quantités x, y et z sont positives.
Or, (y + z)(z + x)(x + y) ≥ 8xyz, donc abc ≥ (b + c – a)(c + a – b)(a + b – c).
En utilisant les angles, la loi des sinus donne abc = 4 RS. La formule de Héron, elle (voir Tangente 180, 2018), donne S2 = p( p – a)( p – b)( p – c). L’inégalité s’écrit alors 4RS ≥ 8S2/p. Enfin, le tour complet du triangle donne S = pr. On en conclut que R ≥ 2r. C’est l’inégalité d’Euler.
Vous pouvez continuer le raisonnement ! Grâce aux propriétés de l’angle inscrit (voir Tangente 178, 2017) et de la puissance d’un point par rapport à un cercle (voir le Cercle, Bibliothèque Tangente 36, 2009), vous retrouverez le théorème d’Euler : le carré de la distance entre les centres des deux cercles est égal à R(R – 2r) qui, fort heureusement, est positif.
Une lumière s’allume
Pour poursuivre l’investigation des techniques disponibles, prenons un entier n au moins égal à 2. On place n lampes autour d’un cercle et on les numérote dans le sens trigonométrique L0, L1, …, Ln–1. Chacune de ces lampes peut être allumée (1) ou éteinte (0). On part de la situation où toutes les lampes sont allumées, puis on applique une suite d’opérations. L’opération Oi consiste à changer l’état de la lampe Li (modulo n) si la lampe Li–1 est allumée, et à ne rien modifier si la lampe Li–1 est éteinte. Par exemple, lorsque n = 3, on part de (1, 1, 1) puis on obtient successivement (0, 1, 1), (0, 1, 1), (0, 1, 0), (0, 1, 0), (0, 1, 0), (0, 1, 1) et à nouveau (1, 1, 1). Toutes les lampes redeviennent allumées après sept opérations.

Reformulons le problème en utilisant la rotation dans le sens horaire, celle qui met à la place de la lampe Li la lampe L i+1 (modulo n). Chaque opération revient à appliquer cette rotation puis l’opération O0. En reprenant l’exemple précédent, l’opération O1 transforme {0, 1, 1} en {0, 1, 1}, ce qui revient à passer à {1, 1, 0} par la rotation, puis à {0, 1, 1} par l’opération O0.
Posons vi = 0 ou 1 selon que la lampe Li est éteinte ou allumée. L’état du système à l’instant j peut être décrit par le polynôme :
Pj (x) = vn–2 + vn–3 x +… + v0 x n–2 + vn–1 x n–1.
De deux choses, l’une.
Soit vn–1 = 0, on a Pj+1(x) = x Pj (x).
Soit vn–1 = 1, alors
Pj+1(x) = 1 + vn–2 x +… + v1 x n–2 + (1 – v0 ) x n–1
= (vn–2x + vn–3x 2 +… + v0 x n–1 + vn–1 x n )
+ (1 + (1 – v0 ) x n–1 – v0x n–1 – vn–1 x n ) = x Pj (x)
modulo x n + x n–1 + 1, car 2v0 = 0 et –1 = 1 modulo 2.
Les restes possibles (en termes techniques, classes de résidus de la congruence) modulo x n + x n–1 + 1 étant en nombre fini, il existe forcément un entier q tel que x q = 1, donc tel que Pj+q (x) = Pj (x). Ainsi, il existe un entier strictement positif T(n) tel que, après T(n) opérations, toutes les lampes redeviennent allumées. Les lecteurs courageux pourront montrer que, lorsque n est de la forme 2 u , toutes les lampes redeviennent allumées après n2 – 1 opérations.
Les jeux de pions
Le problème des soldats de Conway est un jeu à une personne. Il se déroule sur un damier infini divisé par une ligne horizontale qui s’étend indéfiniment. Au-dessus de la ligne se trouvent des cases vides, et en dessous se trouvent un nombre arbitraire de pions (au plus un par case). Comme dans le solitaire, un mouvement consiste en un pion sautant par-dessus un pion adjacent dans une case vide, verticalement ou horizontalement (mais pas en diagonale), et en retirant le pion qui a été sauté. Le but du jeu est de placer un pion aussi loin que possible au-dessus de la ligne horizontale.
Il est possible d’atteindre respectivement les rangées 1, 2, 3 et 4 au-dessus de la ligne horizontale (la croix verte marque la case cible) avec deux, quatre, huit et vingt pions. Sur les schémas, les pions marqués « B » représentent une alternative à ceux marqués « A ».
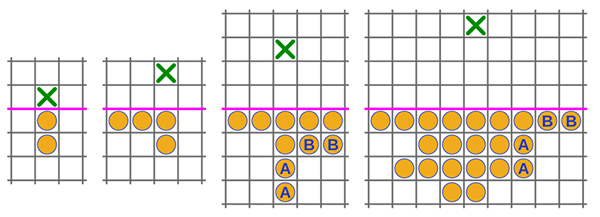
Curieusement, il est impossible d’atteindre la rangée 5 ! Afin de le prouver, introduisons un score. Attribuons la valeur x 0 = 1 à la case cible et la valeur x p à toutes les cases éloignées (horizontalement et verticalement) de p unités de la case cible. Le score d’une configuration est la somme des valeurs des cases occupées par un pion. Par exemple, le score de la deuxième configuration sur le dessin est x 4 + 2 x 3 + x 2. Lorsqu’un pion occupant la case x p saute par-dessus un autre pion, trois cas sont à considérer pour calculer la variation du score, à savoir : quand il se rapproche de la case cible, il augmente de x p–2 (1 – x – x 2 ) ; quand il reste à distance égale, il baisse de x p–1 ; quand il s’éloigne de la case cible, le score monte de x p (x 2 + x – 1).
Choisissons x = φ–1, l’inverse du nombre d’or,
Quel est le score de la configuration initiale ? Avec un nombre fini de pions, il est strictement inférieur à celui de la configuration (théorique) où toutes les cases sous la ligne horizontale seraient occupées par un pion, soit :
[x + 2(x 2 + x 3 + x 4 +… )](1 + x + x 2 + x 3 + x 4 +…). La première parenthèse somme sur la première rangée au-dessous, la seconde sur toutes les rangées au-dessous. Lorsque x = φ –1, on remarque que x 2 + x 3 + x 4 +… = 1. L’expression vaut alors 5 + 3φ–1, environ 6,854, ce qui « laisse de la marge » pour atteindre la rangée 1. Par contre, en la multipliant par x 4, l’expression devient exactement 1, ce qui ne laisse aucune souplesse pour atteindre la rangée 5.
Un dénombrement astucieux
Revenons à une question plus simple en apparence : le dénombrement de coloriages élémentaires. Fixons un entier s ≥ 2. De combien de façons peut-on colorier les six faces d’un cube avec s couleurs (à une rotation près) ?
Afin de répondre à cette question, on peut utiliser le théorème de Pólya, qui est un puissant résultat de combinatoire. Un coloriage est une application f d’un ensemble fini X (les faces du cube) dans l’ensemble C des s couleurs. À chaque couleur c est associée une variable yc. Le poids w ( f ) d’un coloriage f est le monôme produit des yce (c), où chaque exposant e (c) est le nombre des éléments de X de couleur c. On peut s’amuser à suivre les images successives d’un coloriage donné sous l’action du groupe de permutations de X (c’est-à-dire des rotations du cube) ; on parle alors de l’orbite de ce coloriage. Tous les coloriages d’une même orbite sous G ont le même poids. Ceci permet de définir l’inventaire des orbites des coloriages W comme la somme des w ( f ) où f correspond à un coloriage par orbite. Le théorème de Pólya énonce que W est également la valeur prise par le polynôme indicateur des cycles de l’action de G sur X lorsque la variable zi est la somme des yci ; voyons ce que cela signifie dans le cas de deux couleurs (s = 2).
Lorsque s = 2, le polynôme indicateur P en question est
P(t, u) = ((t + u)6 + 3(t + u)2 (t 2 + u 2 ) 2 + 6 (t + u)2 (t 4 + u 4 ) + 6 (t 2 + u 2 ) 3
+ 8(t 3 + u3 ) 2 ) / 24,
soit t 6 + t 5 u + 2t 4 u 2 + 2t 3 u 3 + 2t 2 u4 + tu 5 + u 6. Par exemple, le nombre des coloriages avec quatre faces d’une couleur et deux faces de l’autre vaut le coefficient de t 4 u2, soit 2.
Somme toute, le nombre des coloriages recherché vaut 1 + 1 + 2 + 2 + 2 + 1 + 1, donc 10, ce que l’on vérifie facilement « à la main ».
En généralisant à s couleurs, le polynôme P devient Ps( z1, z 2… zs ) = (( z1 + z 2 +… + zs )6 + 3(z1 + z2 +… + zs )2 (z12 + z 22 +… + zs2 )2 +…) / 24.
En faisant z1 = z 2 = … = zs = 1, les lecteurs courageux trouveront que le nombre des coloriages demandé est
En particulier, on obtient 57, 234, 770, 2 136 coloriages lorsque s vaut successivement 3, 4, 5 et 6.
Les cadets marchent au pas
Un peloton d’élèves officiers forme un carré de dix mètres de côté et ils avancent d’un pas régulier. La mascotte de la compagnie, un petit fox-terrier, part du centre du dernier rang et trotte en ligne droite vers l’avant pour aller au centre du premier rang. Elle revient ensuite à la même allure au centre du dernier rang. À cet instant, les cadets ont avancé de dix mètres exactement. En supposant que le chien trotte à vitesse constante et qu’il ne perd pas de temps en tournant, combien de mètres a-t-il parcourus ? (D’après une question célèbre de Martin Gardner et de Sam Loyd.)
Appelons d le rapport de la distance demandée à vingt mètres, et P la vitesse du peloton. La vitesse du chien est d P. Quand il va vers l’avant, sa vitesse par rapport aux cadets est (d P – P) pendant le temps t1.
Quand il revient vers l’arrière, elle vaut (d P + P) pendant le temps t 2. On a
(d P – P) t1 = (d P + P) t2 = P( t1 + t2 ) = 20.
On en déduit P(20/(d P – P) + 20/(d P + P)) = 0, soit d 2 – 2d – 1 = 0.
La solution positive est
Le chien a parcouru
Les lecteurs courageux pourront chercher la variante du problème dans laquelle la mascotte fait le tour du carré ; on aboutit à un polynôme du quatrième degré.
