Histoires de polynômes

Des polynômes sous les antennes

Comment choisit-on la forme des antennes chargées de réfléchir des rayons incidents et de les concentrer au mieux ? La parabole de foyer F et de directrice d (à une distance p, le paramètre de F ) est l’ensemble des points M équidistants de d et de F. Elle a pour équation  \( y = \dfrac{x^2}{2p}\)   dans le repère orthonormal d’origine son sommet S et d’axe des abscisses sa tangente au sommet.

En un point M d’abscisse a de cette courbe, la tangente a pour équation  \( y = \dfrac{a}{p} x - \dfrac{a^2}{2p}.\)

Elle coupe donc l’axe (SF) de la parabole en  \( \text{T} \left( 0, -\dfrac{a^2}{2p} \right).\)

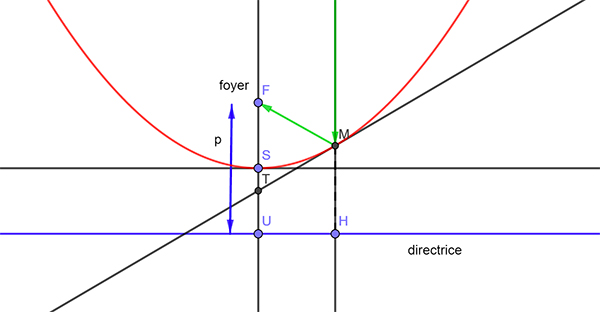
Réflexion sur une antenne parabolique. 

On démontre alors aisément que  \( \text{FT} = \text{MH} = \dfrac{a^2 + p^2}{2p}.\)

Or, par définition de la parabole, MF = MH, donc FT = MF et le triangle FMT est isocèle en F. C’est ici que tout se joue : le rayon (en vert) incident intérieur à la parabole et parallèle à l’axe de celle-ci se réfléchira, selon les lois de la réflexion, de manière que l’angle d’incidence soit égal à l’angle de la réflexion. C’est dire que le rayon réfléchi sera (FM) : tous ces rayons se concentreront en un même point, le foyer de la parabole, qui sera donc le profil idéal pour une antenne ; on n’oubliera pas la présence constante de fonctions polynomiales dans les calculs qui ont mené à ce résultat !

Trajectoires de golfeurs

Un golfeur frappe avec une vitesse v₀ = 40 m/s. La balle est propulsée avec un angle α de 15°. Le joueur suit des yeux la trajectoire et la jolie forme ainsi décrite. Mais au fait, quelle est cette courbe ?

Tentons de décrire la trajectoire de la balle, assimilée à son centre M ( x, y ), dans un repère \( \left( \text{O}, \overrightarrow{i}, \overrightarrow{j} \right)\)  dont l’origine est la position de la balle avant la frappe, l’origine des temps (t = 0) étant l’instant de la frappe du club sur la balle. On suppose négliger tous les frottements, la balle n’étant soumise qu’à son poids.

L’accélération de la balle, représentée par le vecteur \( \overrightarrow{a} = - \overrightarrow{g}\)  (où g est l’accélération de la pesanteur), est la dérivée  \( \dfrac{d\, \overrightarrow{v}}{dt}\) du vecteur vitesse  \( \overrightarrow{v}(t).\)

Les coordonnées de  \( \overrightarrow{a}(t)\) étant (v₀ cos α, –gt + v₀ sin α), comme  \( \overrightarrow{v}(t) = \dfrac{d \,\overrightarrow{\text{OM}}}{dt}, \)  alors :

  \( \left \{ \begin{array}{l} x= (v_0 \cos \alpha)t, \\[0,7mm] y = - \dfrac{1}{2} gt^2 + (v_0 \sin \alpha)t. \end{array} \right.\)

En éliminant t entre ces deux équations, il vient :

  \( y= - \dfrac{1}{2} g \left( \dfrac{x}{v_0 \cos \alpha} \right) ^2 + (v_0 \sin \alpha) \dfrac{x}{v_0 \cos \alpha},\)

soit encore  \( y= - \dfrac{1}{2}g \; \dfrac{x^2}{v^2_0 \cos^2 \alpha} + x \tan \alpha.\)

Le joueur sait désormais que la trajectoire de sa balle, dont l’équation comporte un polynôme de degré 2, est une magnifique parabole et, fort de ces renseignements, il pourra très certainement prévoir combien de temps sa balle prendra avant de revenir au sol, jusqu’à quelle hauteur elle s’élancera, quelle distance horizontale elle aura parcouru…

Balle et club de golf. 

Mettre de l’eau dans son vin

Un négociant peu scrupuleux a mis « un peu » d’eau dans son vin, c’est-à-dire qu’il a prélevé un certain nombre u de litres de son tonneau de 100 litres de vin et les a remplacés par le même nombre de litres d’eau. Puis (tant qu’à faire !) il recommence et, ayant prélevé à nouveau toujours u litres du mélange, il les remplace encore une fois par u litres d’eau. La proportion vin/eau est maintenant 16/9. Combien de litres de vin a-t-il prélevés la première fois ?

Ici encore, on rencontre des polynômes. Le tonneau contient, après le premier prélèvement, u litres d’eau et 100 – u de vin.

Dans les u litres du mélange qu’il retire, se trouvent donc  \( \dfrac{u(100-u)}{100}\) litres de vin et  \( \dfrac{u^2}{100}\) litres d’eau.
 

Après un nouvel ajout de u litres d’eau, le tonneau contient donc  \( 100-u- \dfrac{u(100-u)}{100}\)  litres de vin et  \( \dfrac{u^2}{100}\) litres d’eau.

La proportion de 16/9 fournit donc l’équation  \( \dfrac{100 -2u + \dfrac{u^2}{100}}{2u - \dfrac{u^2}{100}} = \dfrac{16}{9}, \)  soit après réduction u² – 200u + 3 600 = 0, dont la seule solution inférieure à 100 est égale à 20. Le négociant fraudeur avait donc prélevé la première fois vingt litres de vin, et il ne reste en définitive dans son fût « que » soixante-quatre litres de vin pour trente-six litres d’eau.

Optimiser les coûts

En économie, les polynômes ont aussi leur rôle à jouer et ils peuvent intervenir dans de nombreux problèmes de coût. Les économistes distinguent plusieurs sortes de coûts, tous fonction du nombre q d’objets fabriqués : le coût total C(q), le coût moyen C_m, coût moyen de fabrication d’un objet, \( \text{C}_m (q) = \dfrac{\text{C}(q)}{q},\)  et le coût marginal C_ma : ayant fabriqué q objets, quel est le coût de fabrication du suivant ?

Ce coût C_ma est défini par C_ma( q ) = C ( q + 1) – C ( q ).

On peut aussi écrire :  \( \text{C}_{ma} (q) = \dfrac{\text{C}(q+1) - \text{C}(q)}{(q+1) -q}.\)

En définitive, 1 pouvant être considéré comme « petit » par rapport à la quantité q d’objets fabriqués, on peut assimiler q + 1 à q, et C_ma( q ) à sa limite, qui n’est rien d’autre que la dérivée C’(q).

Les courbes représentant C_ma et C_m, qui partent du même point  \( \big(\lim_{q→0} \dfrac{\text{C}(q)}{q} = \text{C}'(0)\big), \) sont en outre telles que le minimum du coût moyen se trouve sur la courbe représentant le coût marginal. En effet, immédiatement avant ce minimum, C_m décroît (le prix du dernier objet fabriqué fait encore baisser la moyenne et la courbe de C_ma se situe en-dessous de celle de C_m) alors que peu après ce minimum, le prix de l’objet suivant devient supérieur au coût moyen.

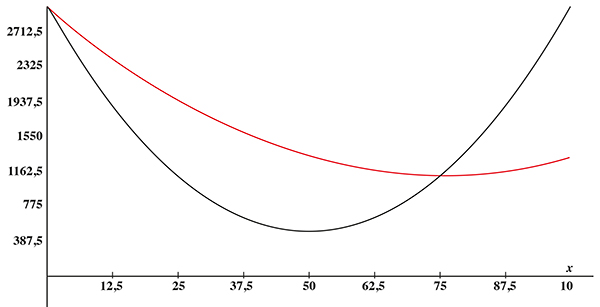
Les courbes de coût marginal (en noir) et de coût moyen (en rouge).

Les polynômes servent à illustrer cette situation des deux courbes : en noir, celle qui représente le coût marginal C_ma( q ) = q ² – 100 q + 3 000 ; en rouge, celle qui représente le coût moyen, C_m( q ) = q ²/ 3 – 50 q + 3 000,
dont on vérifie bien que le minimum de la seconde se situe sur la première.

On peut même en déduire la valeur du coût total puisque C’( q ) = C_ma( q ).
Ainsi, C ( q ) = q ³/ 3 – 50 q ² + 3 000 q, ce qui permettra de l’optimiser.

Des polynômes à la banque

Lors d’une confrontation avec votre banquier, les polynômes peuvent aussi voler à votre secours. Vous empruntez par exemple un capital C₀ sur N mois, à un taux t (fixe) que proposera votre banquier. Ce qui vous intéresse, c’est surtout la mensualité M que vous aurez à payer. Ce M que vous verserez un mois plus tard sert d’une part à rémunérer la banque pour vous avoir prêté C₀ pendant un mois (sous la forme d’un intérêt I₁ = C₀t ), d’autre part (sous la forme M – I₁) à rembourser la banque, à qui vous ne devrez plus que C₁ = C₀ – ( M – I₁) = C0 – ( M – C₀t ) = C₀(1 + t ) – M.

De même, le deuxième mois, votre mensualité M se divisera en intérêts I ₂ = C₁ t et M – I ₂ de capital, et vous devrez encore à la banque C ₂ = C₁(1 + t ) – M = C₀(1 + t ) ² – M(1 + t ) – M, et ainsi de suite… jusqu’au i ^ème mois, où il vous restera une dette de C _i = C_i–1(1 + t) – M.

Le processus itéré donne finalement :

C_i = C₀(1 + t ) ⁱ – M[(1 + t ) ^i–1 + (1 + t ) ^i–2 +… + (1 + t) + 1],

soit  \( \text{C}_i =C_0(1+t)^i −\text{M}\dfrac{(1+t)^i−1}{t}.\)

Comme vous souhaitez avoir tout remboursé à la fin des N mois, écrire C _N = 0 vous donnera le calcul exact de la  mensualité :
\( \text{M} = \dfrac{\text{C}_0t(1+t)^{\text{N}}}{(1+t)^{\text{N}} -1}.\)

Attention aux taux variables !

Imaginons maintenant que le taux t que vous propose votre banquier (voir ci-dessus) est variable et change, par exemple, tous les ans. Du taux initial t ₀, il passe au bout d’un an à une valeur t ₁. Ou bien les variations se reportent sur la mensualité et c’est comme si l’on recommençait un nouveau prêt, ou bien le contrat impose que la mensualité reste constante, et l’on recalcule l’intérêt dû… mais si par malheur le taux s’envole, il se peut que votre mensualité ne couvre pas les intérêts et que votre dette augmente !