À la base du traitement du signal

La géométrie, monde de formes idéales créé par les mathématiciens grecs, a subi une mutation analytique avec l’introduction des coordonnées au XVII^e siècle, notamment par René Descartes. En 1804, Bernard Bolzano introduit des éléments précurseurs du calcul vectoriel, qui sera établi par Giusto Bellavitis (1803–1880) avec son « calcul de l’équipollence ». La définition moderne des espaces vectoriels donnée par Giuseppe Peano est développée au début du XX^e siècle par des mathématiciens comme le Polonais Stefan Banach et le Hongrois Frigyes Riesz. Ils fondent l’analyse fonctionnelle, dans laquelle les fonctions jouent le rôle des vecteurs.

[encadre]

Le produit scalaire

Pour un espace vectoriel E sur le corps K, le produit scalaire, ou produit intérieur, fait correspondre à deux vecteurs \( \overrightarrow{u}\) et  \( \overrightarrow{v}\) de E un scalaire, c’est-à-dire un élément de K, noté \( \overrightarrow{u} \cdot \overrightarrow{v}.\)

Cette composition est symétrique \( (\overrightarrow{u} \cdot \overrightarrow{v} = \overrightarrow{v} \cdot \overrightarrow{u})\)  et linéaire par rapport à chacun de ses composants (au sens que \( (\alpha \overrightarrow{u} + \beta \overrightarrow{v}) \cdot \overrightarrow{w} = \alpha (\overrightarrow{u} \cdot \overrightarrow{w}) + \beta (\overrightarrow{v} \cdot \overrightarrow{w})\)  ), ce qui justifie le terme « produit », par analogie avec les propriétés du produit réel.

Le produit scalaire d’un vecteur par lui-même est égal au carré de sa norme et doit donc être positif  \( (\overrightarrow{u} \cdot \overrightarrow{u} = \| \overrightarrow{u} \| ^2 ≥0)\)  et défini ( \( \| \overrightarrow{u} \| =0\) si, et seulement si, \( \overrightarrow{u} = \overrightarrow{0}\) ). On dit que le produit scalaire est une forme bilinéaire, symétrique, définie, positive. Ces propriétés sont devenues la définition, et toute forme bilinéaire, symétrique, définie, positive s’appelle un produit scalaire. 

[/encadre]

Une géométrie des fonctions

À cette époque, John von Neumann crée les espaces de Hilbert, espaces fonctionnels qui peuvent être de dimension infinie. Cette structure fondamentale s’applique aussi bien à des vecteurs en géométrie de toute dimension qu’à des ensembles de suites, de polynômes ou de solutions d’équations différentielles. Ces espaces bénéficient des fonctionnalités et du vocabulaire de la géométrie vectorielle, et sont donc pourvus d’un produit scalaire (voir encadré). On ne considérera que des espaces euclidiens, à savoir des espaces vectoriels sur le corps des nombres réels.

Les fonctions, vecteurs de ces espaces fonctionnels, doivent être stables par combinaison linéaire. C’est le cas, par exemple, des fonctions continues : si f et g sont deux telles fonctions et α et β deux réels, alors α f + βg est elle-même une fonction continue. L’intégration, opération linéaire qui fait correspondre à une fonction un scalaire, est une bonne candidate pour définir un produit scalaire. On obtient par exemple un produit scalaire sur l’ensemble des fonctions numériques, continues et intégrables sur un intervalle I du corps des réels avec la forme bilinéaire symétrique \( \langle f\, | \, g \rangle = \int_{\text{I}} f (t)\, g(t)\, dt .\)

La norme associée,  \( \| f \| _2 =\sqrt{ ∫_{\text{I}} |f (t) |^2\, dt},\)  est définie pour les fonctions appartenant à l’ensemble noté L², des fonctions de carré intégrable (voir encadré). Cet espace est particulièrement utilisé en physique car il correspond aux phénomènes d’énergie finie. En effet, la plupart des expressions de l’énergie en physique sont proportionnelles, via un coefficient d’inertie, au carré d’une variable caractéristique :

la vitesse v pour l’énergie cinétique  \( \text{E}_c = \dfrac{1}{2} mv^2,\)

le champ électrique E pour la densité d’énergie électromagnétique  \( e_e = \dfrac{1}{2} \varepsilon_0 \text{E}^2,\)  etc.

Comme en géométrie euclidienne, il est alors formellement possible de définir l’angle  \( \Theta (f, g)\) de deux fonctions f et g par l’expression  \( \cos \big[ \Theta (f, g)\big] = \dfrac{ \langle f, g \rangle}{\| f \| _2 \, \| g \| _2}.\)

On a bien  \( \big| \cos \big[ \Theta (f, g)\big] \big| \le1\)  par l’inégalité de Cauchy–Schwarz, qui montre que  \( \big| \langle f, g \rangle \big| \le \| f \| _2 \, \| g \| _2. \)

En particulier, deux fonctions telles que   \( \langle f \, | \, g \rangle =0\)  sont dites orthogonales.

Le poids des familles 

Déterminons des bases polynomiales orthogonales sur lesquelles on décomposera des fonctions de L², tout comme on décompose un vecteur du plan sur une base orthonormée. Tout polynôme  \( \text{P}_n(x) = \sum^n_{k=0} a_k x^k\)  de degré inférieur ou égal à n est déterminé par ses n + 1 coordonnées (a_k )_{k = 0,1…n} dans la base de monômes (x ^k )_{k = 0,1…n} .

L’ensemble E_n de ces polynômes constitue donc un espace vectoriel de dimension n + 1, de structure en tout point identique à l’espace ℝ^n +1. Parmi l’infinité de produits scalaires dont on peut munir l’espace E_n pour lui conférer une structure euclidienne, intéressons-nous aux produits  \( \langle f\, | \, g \rangle _p= \int^1_{-1} f (t)\, g(t)\, p(t) \, dt,\)  avec une fonction poids p (c’est-à-dire une fonction continue positive non nulle).

À chaque fonction poids p du produit scalaire  \( \langle \, | \, \rangle _p\)  est associée une famille de polynômes orthogonaux.

Les plus utilisés en traitement du signal portent les noms des mathématiciens

Legendre ( p ( t ) = 1),

Tchebychev (  \( p(t) = 1 / \sqrt{1-t^2},\) ) ; en modifiant l’intervalle d’intégration,

on obtient aussi ceux de Laguerre sur [0, +∞[ avec p ( t ) = e^–t

et ceux de Hermite sur ]−∞, +∞[ avec p ( t ) = exp (– t ² ).

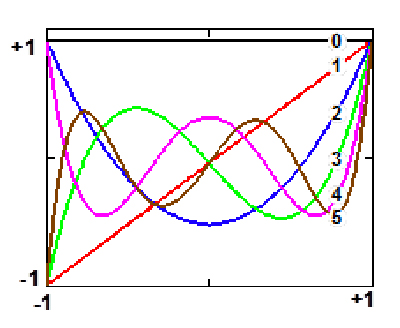
Polynômes de Legendre d’ordre 0 à 5.

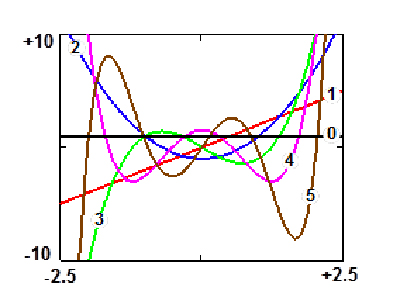
Polynômes de Hermite H_n / 2ⁿ d’ordre 0 à 5.

Polynômes de Laguerre d’ordre 0 à 5.

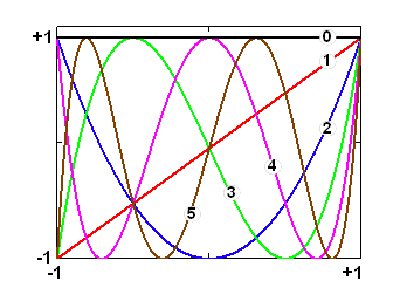
Polynômes de Tchebychev T_n de première espèce d’ordre 0 à 5.

Il suffit de diviser ces polynômes par leur norme  \( \| \; \| _p\) pour obtenir des bases orthonormées de E_n pour chaque produit scalaire  \( \langle \, | \, \rangle _p\) . Cette orthogonalité ne dépend pas de la dimension de E_n ; elle est donc valable pour l’ensemble E_∞ de tous les polynômes, qui est de dimension infinie.

De même que l’on peut toujours trouver une fraction « aussi proche qu’on veut » d’un nombre irrationnel (l’ensemble des rationnels ℚ est dense dans ℝ), l’ensemble des polynômes est dense dans l’ensemble des fonctions continues. Les polynômes orthogonaux P_n permettent alors d’expliciter la meilleure approximation d’une fonction  f au sens des moindres carrés, en calculant les coefficients  \( a_n = \dfrac{ \langle f\, | \, \text{P}_n \rangle _p}{ \| \text{P}_n \| ^2_p}.\)

L’approximation  \( f_n= \sum^n_{k=0} a_n\, \text{P}_n\) d’ordre n, qui est telle que  \( \langle f_n\, | \, \text{P}_n \rangle _p = \langle f\, | \, \text{P}_n \rangle _p , \)   converge donc vers f , au sens que  \( \lim_{n→+∞} \| f -f_n \| _p =0.\)  

Ces importantes familles de polynômes orthogonaux proviennent souvent d’une équation différentielle (dite de Sturm–Liouville), qui a pour expression
( 1 − x ²)  y′′ − 2 xy′ + n ( n + 1) y = 0 pour les polynômes de Legendre. Cette équation apparaît en mécanique classique, en mécanique quantique (spin de l’électron), en électromagnétisme, et en général dans les problèmes présentant une symétrie sphérique.

La figure suivante illustre les différentes approximations d’un contour à l’aide d’une décomposition en polynômes de Legendre. L’ordre 0 est un cercle donnant le rayon vecteur moyen. Le contour présentant une oscillation d’ordre 3, il faut « attendre » cet ordre pour avoir une approximation « correcte » de sa forme. À l’ordre 4, l’écart entre la courbe référence et son approximation est inférieur au demi-pourcent.

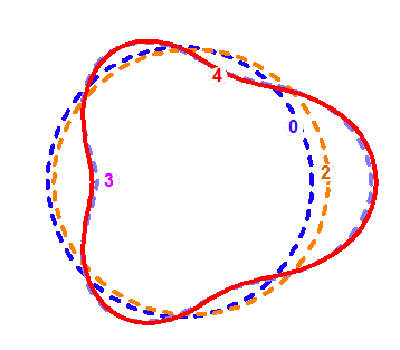
Approximations polaires d’un contour par polynômes de Legendre
(seuls les ordres 0, 2, 3 et 4 sont représentés).

Les polynômes de Hermite, comme ceux de Laguerre, ont de nombreuses applications en physique mathématique et en mécanique quantique. Les polynômes de Tchebychev permettent d’effectuer des interpolations, et sont utilisés dans certains problèmes trigonométriques puisque T_n(cos θ) = cos(nθ) pour tout θ compris entre 0 et 2π. Au-delà de ces cas particuliers, toutes ces bases polynomiales sont abondamment utilisées en théorie de l’approximation, en analyse numérique et en traitement du signal, comme récemment pour la compression des signaux d’électrocardiogramme pour une meilleure transmission en télémédecine.

[encadre]

L’inégalité de Hölder

Les espaces fonctionnels L^p contiennent des fonctions  f de puissances p^ème intégrable (en identifiant les fonctions égales presque partout), c’est-à-dire telles que \( \| {f} \| _p < \infty\) , en notant  \( \| {f} \| _p = \left( \int_{-\infty} ^{+\infty} | f (t)| ^p dt \right)^{1/p}\)  la norme de f .

En considérant deux nombres p et q conjugués, c’est-à-dire tels que  \( \dfrac{1}{p}+ \dfrac{1}{q} =1,\)   on obtient l’inégalité de Hölder :  \( \| {f \cdot g} \| _1 \le \| {f} \| _p \| {g} \| _q,\)  pour f dans L^p et g dans L^q.

Pour p = q = 2, on trouve la célèbre inégalité de Cauchy–Schwarz :  \( \| {f \cdot g} \| _1 \le \| {f} \| _2 \| {g} \| _2.\)

[/encadre]