Approcher efficacement les fonctions

Quels sont les moyens de calcul à notre disposition, que l’on utilise un ordinateur ou non ? Sur le corps des nombres réels, comme sur celui des nombres complexes ou même d’autres plus abstraits, on sait effectuer quatre opérations élémentaires : addition, soustraction, multiplication et division. Si une variable x est impliquée, cela nous mène aux fractions rationnelles, c’est-à-dire aux polynômes et à leurs quotients. À ce niveau, la question devient : peut-on remplacer une fonction quelconque par un polynôme ?

De l’approximation d’une fonction

Posée dans toute sa généralité, la réponse est bien entendu négative. Il est nécessaire d’imposer des conditions à la fonction et à son domaine de définition. On doit au mathématicien allemand Karl Weierstrass le théorème le plus simple sur la question : une fonction  f continue sur un segment [a, b] peut être approchée d’aussi près que l’on veut par un polynôme P.

Karl Theodor Wilhelm Weierstrass (1815–1897).

Plus précisément, étant donné une fonction f continue sur [a, b] et  \( \epsilon\) > 0 (aussi petit que l’on veut), il existe un polynôme P tel que | f (x) – P (x) | <  \( \epsilon\)  pour tout x appartenant à l’intervalle [a, b]. L’idée la plus simple pour trouver un tel polynôme (et donc démontrer le théorème) est d’interpoler la fonction f .

Le problème de l’interpolation polynomiale est le suivant : on connaît une fonction par ses valeurs y_i en un certain nombre fini de points x_i, et on cherche un polynôme P prenant les mêmes valeurs aux mêmes points, c’est-à-dire tel que P(x_i) = y_i pour tout i. Ce problème possède une interprétation géométrique en termes de courbe (celle d’équation y = P(x)) passant par les points donnés.

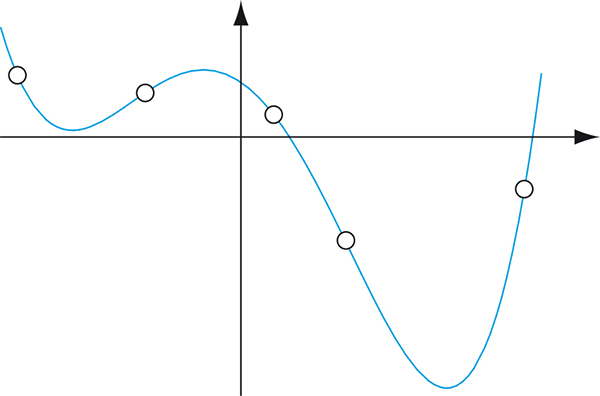
Par cinq points, il passe une et une seule courbe
dont l’équation est un polynôme de degré au plus 4.

La condition se traduit par autant d’équations qu’il y a de points. A priori, il est possible de déterminer P de façon unique s’il correspond au même nombre de paramètres, ce qui se produit si l’on impose à P d’être de degré au plus égal au nombre de points, moins un. En effet, la question équivaut alors à un système linéaire ayant autant d’équations que d’inconnues à résoudre, ce qui, sauf cas exceptionnel, a toujours une solution unique.

Afin d’être plus concret, considérons trois points (x₀, y₀), (x₁, y₁) et (x₂, y₂), et cherchons un polynôme du second degré, sous la forme P (x) = a x² + b x + c, tel que P (x₀) = y₀
P (x₁) = y₁ et P (x₂) = y₂. La question revient à résoudre le système suivant :

\( \left\{ \begin{array}{cc} ax^2_0+bx_0+c=y_0, \\ ax^2_1+bx_1+c=y_1, \\ ax^2_2+bx_2+c=y_2. \end{array} \right.\)

Un calcul algébrique fastidieux mais tout à fait élémentaire montre que ce système de trois équations à trois inconnues possède une solution unique. Une idée plus intuitive est de considérer a priori les trois polynômes du second degré L₀, L₁ et L₂ valant 1 en l’un des points et 0 en les deux autres, soit : 

\( \mathrm{L}_0(x)=\frac{(x-x_1)(x-x_2)} {(x_0-x_1)(x_0-x_2)}\)   (valant 1 en x₀ et 0 en x₁ et x₂), 

\( \mathrm{L}_1(x)=\frac{(x-x_0)(x-x_2)} {(x_1-x_0)(x_1-x_2)}\)  (valant 1 en x₁ et 0 en x₀ et x₂), et  

\( \mathrm{L}_2(x)=\frac{(x-x_0)(x-x_1)} {(x_2-x_0)(x_2-x_1)}\)  (valant 1 en x₂ et 0 en x₀ et x₁).
Ces trois polynômes L₀, L₁ et L₂ sont appelés polynômes de Lagrange, du nom du mathématicien Joseph-Louis Lagrange (1736–1813).

On remarque alors que le polynôme P de degré au plus 2 défini par P = y₀ L₀ + y₁ L₁ + y₂ L₂ vérifie précisément, par construction, P(x₀) = y₀, P(x₁) = y₁ et P (x₂) = y₂ comme cherché, ce qui assure l’existence du polynôme interpolateur.

Son unicité se démontre en considérant un second polynôme interpolateur Q. Le polynôme R = P – Q de degré au plus 2 s’annule alors aux trois points x₀, x₁ et x₂, ce qui implique sa nullité puisqu’un polynôme de degré 2 non nul possède au plus deux zéros. Ainsi, P = y₀ L₀ + y₁ L₁ + y₂ L₂ est l’unique polynôme de degré au plus 2 tel que P (x₀) = y₀, P (x₁) = y₁ et P (x₂) = y₂, et on l’a déterminé sans effectuer aucun calcul. Il est appelé le polynôme interpolateur de Lagrange des points (x₀, y₀), (x₁, y₁) et (x₂, y₂).

Le phénomène de Runge

L’approximation des fonctions est un problème légèrement différent de l’interpolation. Un segment [a, b] et une précision ´ étant donnés, il s’agit de trouver un polynôme P ne s’« éloignant pas » (sur [a, b]) de plus de ´ de la fonction étudiée.

Dans ce but, on peut par exemple choisir un grand nombre de points de son graphe, d’abscisses uniformément réparties sur [a, b], et les interpoler. Malheureusement, le polynôme d’interpolation peut ne pas convenir ! Par exemple, en interpolant la fonction   \( f(x)=\frac{1}{1+25x^2}\)   sur [–1, 1] avec cinq points d’interpolation uniformément répartis (en bleu), on obtient la courbe en rouge, et avec neuf points, la courbe en vert. Plus il y a de points, plus l’approximation est mauvaise ! Ce comportement étrange est appelé phénomène de Runge, du nom de Carl Runge, le mathématicien qui l’a découvert. Ce phénomène s’apparente à celui de Gibbs (voir le dossier « La discontinuité », Tangente 192, 2020).

Illustration du phénomène de Runge.

Une façon d’y remédier est d’utiliser comme abscisses d’interpolation les zéros des polynômes de Tchebychev, qui renforcent l’influence des extrémités de l’intervalle, là où se situe le phénomène de Runge. Ainsi, sur [–1, 1], il s’agit des nombres  \( \cos (\frac{2k+1}{2n}\pi )\)  où k varie de 0 à n – 1.

Il existe d’autres méthodes d’approximation qui font également appel à des polynômes. Chacune a son domaine d’application privilégié. Par exemple, les développements en série entière sont utiles pour résoudre certaines équations différentielles linéaires.

[encadre]

Carl Runge, inspiré par Planck et Weierstrass

Bien que né en 1856 à Brême dans le nord de l’Allemagne, Carl Runge s’inscrit à l’université de Munich pour y suivre des études… littéraires. Il se lie d’amitié avec le futur célèbre physicien Max Planck (1858–1947), étudiant lui aussi dans la capitale de la Bavière. Il se tourne alors vers les sciences et les deux amis se rendent à Berlin en 1877 suivre les cours de Karl Weierstrass.

Runge obtient son doctorat en 1880 pour une thèse sur la géométrie différentielle. Professeur à Hanovre de 1886 à 1904, il occupe la chaire de mathématiques appliquées à l’université de Göttingen jusqu’à sa retraite en 1925. Il s’éteint deux ans plus tard, victime d’une attaque cardiaque.

Les travaux de Runge sont à la croisée des mathématiques et de la physique. Il étudie les expressions numériques de solutions d’équations algébriques, les méthodes de solutions approchées d’équations différentielles (dont l’une, élaborée avec son compatriote Martin Kutta, améliore celle de Leonhard Euler) et il développe différents algorithmes dans le domaine. En 1901, il met en évidence le phénomène qui porte son nom suivant lequel l’interpolation polynomiale d’une fonction continue sur un segment peut énormément diverger au voisinage de ses bornes. Éclectique, Carl Runge effectue également des travaux en spectroscopie astronomique et en géodésie, et il garde toute sa vie un intérêt pour la philosophie.  B.H.

Carl David Tolmé Runge (1856–1927). 

[/encadre]