
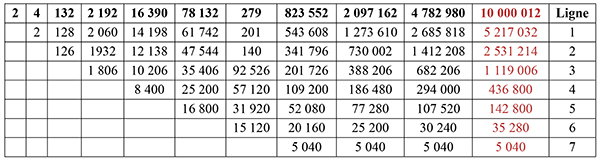
Si l’on vous donne une suite qui commence par 2, 4, 132, 2 192, 16 390, 78 132, 279 944,
823 552, 2 097 162, 4 782 980, comment faire pour trouver le terme suivant ? L’astuce est de faire la différence entre deux termes successifs. Puis de recommencer avec les nouveaux nombres obtenus. On s’arrête dès que la ligne ne contient qu’un terme unique (ici, c’est la ligne 7, qui ne contient que le terme 5 040). On en déduit que l’on a affaire aux valeurs prises par un polynôme de degré 7.
Maintenant, comment trouver le terme suivant ?
Chaque terme est obtenu en faisant la différence entre le terme
directement au-dessus et celui au-dessus à gauche.
La colonne en rouge se remplit de bas en haut, en partant
de 5 040, jusqu’à l’obtention du nombre cherché, 10 000 012.
Simplement en propageant les différences :
35 280 = 30 240 + 5 040,
puis 142 800 = 107 520 + 35 280,
ensuite 436 800 = 294 000 + 142 800,
on en déduit 1 119 006 = 682 206 + 436 800,
suivi de 2 531 214 = 1 412 208 + 1 119 006,
qui conduit à 5 217 032 = 2 685 818 + 2 531 214,
et finalement 10 000 012 = 4 782 980 + 5 217 032.
Pour compléter le tableau, on ne fait que des additions, malgré le degré élevé du polynôme : c’est la méthode des différences finies. Ces remarques vont donner l’idée à Charles Babbage (1791–1871) de la machine à différence.
Mécaniser le calcul
À la fin du XVIII e siècle et au début du XIX e, les besoins en calculs sont immenses. En 1800, les calculs se font avec des tables de logarithmes et trigonométriques ; encore faut-il disposer de telles tables, et qu’elles soient correctes…
Le Bureau des longitudes va produire l’une de ces tables en 1801, sous la houlette de Gaspard de Prony (1755–1839). Cet ingénieur et encyclopédiste va organiser le travail de la façon suivante. Une première équipe constituée de mathématiciens (dont Adrien-Marie Legendre et Lazare Carnot), sous sa direction, met en place les formules utilisées et les données initiales. Une seconde équipe, emmenée par Jean-Guillaume Garnier, prépare les pages de calculs à partir des formules (essentiellement des polynômes) de la première équipe. Enfin, une troisième équipe de cent cinquante à deux cents personnes remplit les pages en faisant les additions et soustractions. D’après le mathématicien et homme politique Charles Dupin (1784–1873), parmi ces calculateurs se trouvent de nombreux anciens perruquiers, mis au chômage par l’abandon de la mode des perruques à l’époque révolutionnaire ! Les calculs effectués reviennent à la deuxième équipe, qui les vérifie et les finalise : les résultats sont réalisés « en double » et validés seulement s’ils sont identiques. De Prony se serait inspiré d’écrits de l’économiste Adam Smith sur la division du travail appliquée à la fabrication d’épingles… Malheureusement, ces tables ne seront pas publiées car trop volumineuses.
Charles Babbage connaît les travaux de de Prony, qui est alors en contact étroit avec les savants britanniques. Babbage a bien compris que le maillon faible de cette chaîne (au sens industriel) de calculs est la réalisation des additions. Il propose d’automatiser ces dernières. Pour ce faire, il dessine en 1821 la « machine à différence », qui sera destinée à calculer des valeurs de polynômes par différences finies. Seule une partie de cette machine sera construite, déjà par manque de fonds, ensuite car Babbage en modifie sans arrêt les plans.
En 1836, Babbage conçoit une machine analytique, véritable ordinateur mécanique avant la lettre, capable de lire son programme sur des cartes perforées ! En 1842, il dessine une deuxième machine à différence, version au design simplifié et amélioré. Mais revenons à notre suite du début, qui correspond en fait aux valeurs du polynôme X 7 + X + 2 (voir le tableau ci-dessous).
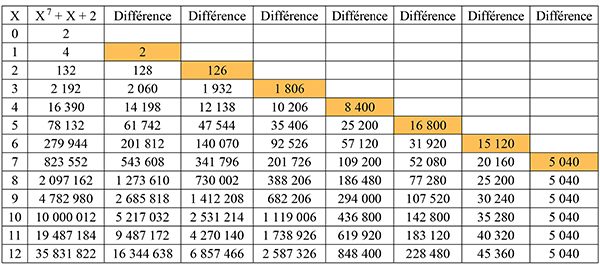
Il s’agit de calculer à la main les sept termes en orange, que l’on reporte dans le tableau. Puis, à chaque étape, on ajoute les deux termes hachurés, ce qui donne le terme en vert. Comme ici c’est un polynôme de degré 7, il faut sept étapes pour obtenir la ligne bleue qui correspond à X = 1 (voir le tableau suivant).
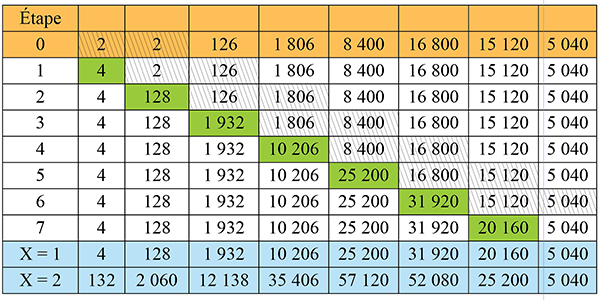
La machine de Babbage possède une structure matricielle : chaque nombre est une colonne. On a autant de lignes que de colonnes, et autant de colonnes que le degré du polynôme. Les adeptes de belle mécanique comprendront ainsi le fonctionnement de l’additionneur : dans une colonne, chacun des nombres est un tambour dont on peut débrayer la couronne pour afficher un nouvel entier. L’addition se produit en embrayant un additionneur mécanique entre deux colonnes successives. Ce mécanisme physique propage la retenue à l’étage supérieur. Un mécanisme auxiliaire recentre les roues dentées pour éviter les coincements.
Une fois que l’on a calculé une ligne, on n’a plus besoin de mémoriser les précédentes. De même, une fois que l’on a calculé une colonne C, la valeur précédente dans C est devenue inutile ; il est donc possible de réaliser le calcul directement dans C.
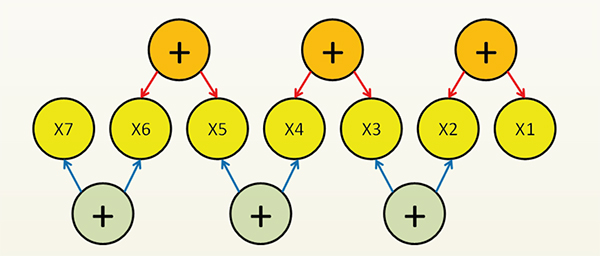
L’inconvénient de cette méthode est que, pour calculer chaque ligne, il faut autant d’étapes que le degré du polynôme. Babbage va optimiser le processus en entrelaçant les additions afin de calculer une ligne en seulement deux étapes, indépendamment du degré du polynôme.
Cette méthode nécessite le pré-calcul de plus de termes mais est beaucoup plus efficace ! Première étape : on somme les termes de même couleur sur la même ligne. Le résultat vient dans la ligne suivante sous le terme de gauche (flèches rouges). Seconde étape : on somme les termes hachurés sur la même ligne. Le résultat vient dans la ligne suivante sous le terme de gauche (flèches bleues).

Ce calcul, plus efficace, est aussi plus facile à implémenter : il suffit de construire deux groupes d’additionneurs qui seront embrayés alternativement.
De son vivant, Babbage ne construisit qu’une ébauche de sa première machine à différence, et sa seconde ne restera qu’à l’état de plan. La machine analytique nous aurait plongés dans un monde informatique, mais mécanique, dès le milieu du XIX e siècle !