Après les formes classiques construites à partir de maquettes, d’autres formes encore plus fluides et plus osées sont nées de la puissance de nouveaux outils mathématiques élaborés, qui ont fait littéralement disparaître les chiffres des cabinets d’architecture pour les remplacer par des algorithmes. Ces formes architecturales, toutes plus grandioses et inattendues les unes que les autres, offrent dans le monde entier une grande variété de design.

Château d’eau des Pialoux à La Roche de Glun (Drôme).

Les coniques en majesté

Si l’architecture classique a eu tendance à limiter le tracé de ses surfaces au cylindre, au cône et à la sphère, on voit dès le XVIII ^e siècle apparaître des surfaces un peu plus originales. Les architectes d’aujourd’hui peuvent aller toujours plus loin dans ce sens grâce à la conception par ordinateur.

Les surfaces les plus faciles à réaliser en béton armé sont les surfaces dites réglées, obtenues par réunion des droites d’une même famille, généralement obtenue par un procédé géométriquement simple. Il peut s’agir, par exemple, de la torsion des génératrices d’un cylindre pour décrire un hyperboloïde, engendré par la rotation d’une droite autour d’un axe, comme l’illustre le château d’eau ci-contre. Certaines des sections planes de cette surface élancée sont des hyperboles.

Le circuit-test de Wolfsburg.

Une autre forme au délié spécialement esthétique, dont les sections planes sont également des coniques, est celle du paraboloïde hyperbolique, une structure en forme de selle de cheval magnifiquement illustrée par le circuit-test de l’usine Volkswagen de Wolfsburg (Allemagne), dont les lignes dynamiques rappellent les virages d’un circuit de course automobile. Certaines des sections planes de cette surface sont des paraboles, d’autres des hyperboles, d’où le nom mathématique de cette surface.

En 1525 déjà, Albrecht Dürer, dans son Underweysung der Messung (« Les instructions pour la mesure »), imaginait des colonnes torses d’une invraisemblable audace. Il ne faisait que préfigurer les découpes osées de l’architecture « paramétrique » d’aujourd’hui, où les avancées technologiques sont telles que non seulement les techniques de construction évoluent, mais le mode même de création de l’architecte, avec la conception assistée par ordinateur, change. On peut très vite modifier « en un clic de souris » la forme d’une colonne, là où Dürer mettait sans doute des heures à faire la même chose. C’est ainsi que l’architecture paramétrique a pris le pas sur le « papier-crayon », ce qui rend possible de donner aux bâtiments ces allures aériennes qui deviennent vite compliquées.

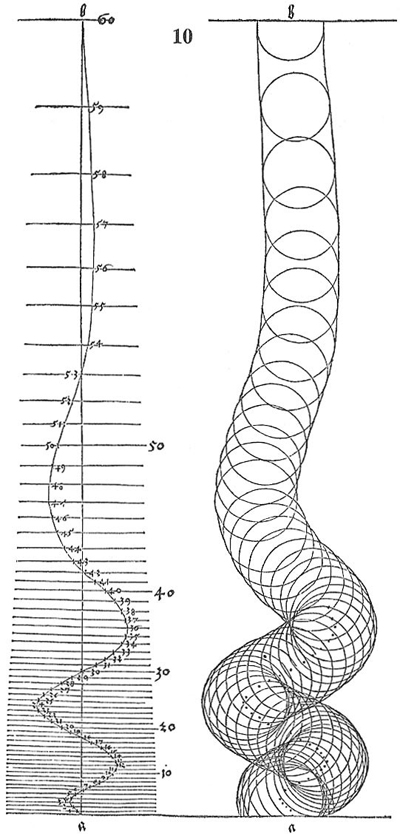
Un croquis de l’Underweysung der Messung de Dürer (colonne torse)

Pour le dire d’abord avec des courbes, on peut par exemple, dans le plan, rien qu’en introduisant quelques valeurs de deux paramètres, ici les nombres réels a et b, changer le cercle d’équation (x (t) = cos t, y (t) = sin t) en l’ellipse d’équation
(x (t) = a cos t, y (t) = b sin t).

Avec des surfaces de l’espace ensuite : celle qui a pour équation z = exp(– a (x ² + y ²)) devient par exemple, selon les valeurs croissantes de a, un « chapeau » de plus en plus pointu. Il suffit donc au concepteur d’une seule équation pour décrire autant de formes qu’il souhaite. La tour New York by Gehry du 8 Spruce Street à New York, conçue par l’architecte américano-canadien Frank Gehry et achevée en 2011, est un magnifique exemple de ces modifications qui donnent au bâtiment sa structure féérique.

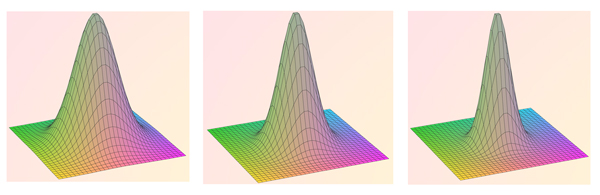
Les tracés successifs,  pour a = 3, a = 9 et a = 15,
produisent des « pointes » de plus en plus en plus acérées.

Oser les bulles

D’autres surfaces, encore plus fantaisistes, sont conçues aujourd’hui, renouvelant chaque jour un peu plus les concepts architecturaux. Lorsqu’ils ont conçu leur projet de stade nautique pour les Jeux olympiques de Pékin en 2008, les architectes des cabinets australien PTW et britannique Ove Artup avaient une seule idée en tête : pour pouvoir cohabiter avec le très original « Nid d’oiseau » du stade olympique, une structure bleue évoquant l’eau était privilégiée. C’est ainsi qu’ils ont osé les bulles de surface de leur « cube d’eau  ».

Le cube d’eau des J.O. de Pékin en construction.

Les mathématiques sont venues plus tard, lorsqu’ils ont voulu sortir de l’ordinaire avec leur projet et se sont demandé : « Quelle structure topologique autre qu’une trame banalement triangulaire peut bien remplir l’espace ? » C’est alors qu’ils se sont intéressés aux bulles de savon et aux règles édictées par le physicien belge Joseph Ferdinand Plateau en 1873 concernant la structure d’une mousse de bulles de savon. Ils ont découvert l’efficacité de la solution proposée en 1993 par le professeur Denis Weaire (Trinity College, Dublin) et son assistant Robert Phelan : une structure à la fois profondément régulière, mais qui, vue sous un certain angle, apparaissait très « aléatoire » (voir FOCUS).

Il restait alors à réaliser physiquement la structure complète de la piscine olympique : les quatre mille polyèdres auront des surfaces en Teflon légèrement bombées (à cause des exigences de Plateau), véritables bulles gonflées en permanence. Les polyèdres à quatorze faces sont empilés, collés les uns aux autres par leurs faces hexagonales, pour former les colonnes dans trois directions d’un réseau cubique, à l’intérieur duquel viennent s’insérer les dodécaèdres, répétant par translation cette structure de quinze polyèdres, sans que le résultat final apparaisse monotone. Un exploit grandiose !

Avec les bâtisseurs du Moyen Âge, les églises sont devenues cathédrales. Avec des architectes comme Buckminster Fuller, les sphères sont devenues géodes. Avec Zaha Hadid, récemment disparue, ou Frank Gehry, les bâtiments sont devenus de véritables usines à rêve…

New York by Gehry.