Centrales, tours et châteaux d’eau

 En faisant tourner une droite autour d’un axe, on obtient une famille de droites qui définissent une surface réglée. L’étonnant est qu’il y a en général deux familles distinctes qui permettent d’obtenir une même surface, laquelle peut ainsi être construite de manière très rigide.

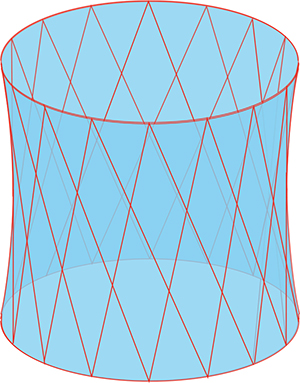
Hyperboloïde de révolution à une nappe, avec ses deux familles de génératrices.

En voyant cette figure, on reconnaît une surface utilisée en particulier comme tour de refroidissement des centrales nucléaires ou thermiques, ainsi que comme château d’eau. Une tour rencontrée à Boukhara, en Ouzbékistan, en face de la forteresse, a aussi cette même forme. Elle a été construite en 1927 par Vladimir Choukhov (voir article "Vladimir Choukhov, le Gustave Eiffel russe") pour servir de château d’eau. Désaffectée à la fin des années quarante, elle est devenue un café, qui a fermé après un accident mortel. Elle vient d’être rachetée par des Français pour devenir un point d’observation ! Un ascenseur est prévu pour y accéder.

La tour de Choukhov à Boukhara,
et ses deux familles de droites génératrices.

Tabourets et toits

Beaucoup de constructions contemporaines sont en béton armé. Les armatures métalliques privilégient les surfaces construites au moyen de lignes droites, comme le plan ou le cylindre, mais d’autres possibilités existent (pensez à la tour de Choukhov, dont le nom technique est hyperboloïde de révolution à une nappe). On l’obtient en effet aussi en faisant tourner une hyperbole autour de l’un de ses deux axes de symétrie (l’autre donnerait naissance à l’hyperboloïde à deux nappes). Au Népal, les tabourets traditionnels sont fabriqués avec des morceaux de bambous de même longueur, liés par des cordes en plusieurs endroits, et décalés du même angle, dans un sens comme dans l’autre, produisant également des hyperboloïdes de révolution.

Sur ce tabouret traditionnel népalais,
les deux familles de génératrices
comme l’hyperbole du contour
sont particulièrement visibles.

Une autre variante possible consiste à prendre deux droites au lieu de deux cercles pour définir le bord. On parle alors de paraboloïde hyperbolique, car on peut y voir des paraboles et des hyperboles. On s’en sert notamment pour fabriquer des toits.

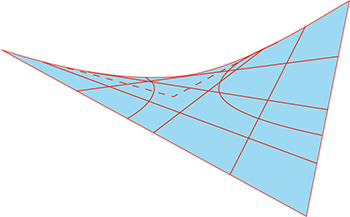
Paraboloïde hyperbolique avec génératrices, paraboles et hyperboles.

Les rampes hélicoïdales

On retrouve des surfaces réglées dans les rampes hélicoïdales desparkings souterrains. Un exemple historique se trouve au château d’Amboise (Indre-et-Loire). Pour en fabriquer une, on part d’un point mobile A décrivant un axe vertical à vitesse constante et d’une droite horizontale mobile D passant par A, tournant autour de l’axe à vitesse angulaire constante.

Rampe hélicoïdale dans un parking souterrain.

Moins utile mais plus intrigante, le ruban de Möbius est aussi une surface réglée puisque qu’il consiste à partir d’une bande de papier qui, collée à l’endroit donne un cylindre, mais donne une surface à une seule face quand on la colle à l’envers. De nombreux sculpteurs s’en sont inspirés.