Tout a commencé par la vision géométrique d’un chimiste écossais, Alexander Crum Brown (1838–1922). L’homme est surtout connu pour avoir inventé la représentation actuelle des composés organiques, dans laquelle les atomes sont représentés par des sphères reliées par des segments qui symbolisent les liaisons chimiques. C’est également lui qui a découvert la double liaison de la molécule d’éthylène.

Alexander Crum Brown (1838–1922).

Mais il est aussi le premier à s’être intéressé au… tricotage de formes géométriques. Très jeune, il construit une machine à tisser et s’intéresse aux nœuds et aux systèmes de tricotage élaborés. Invalide à la fin de sa vie, il retourne à cette passion pour le tricot, qui lui permet de visualiser des nœuds et des surfaces à trois dimensions.

Faces avant et arrière d’un des tricots de Brown, constitué de trois couches dont les intersections ont des couleurs différentes.

Des défis topologiques

La technique de tricotage utilisée par Brown nous est inconnue, mais l’idée a eu des continuateurs, notamment la mathématicienne américaine Sarah-Marie Belcastro, professeure au Smith College à Northampton (Massachusetts). Inspirée par un ouvrage du mathématicien britannique Miles Reid, elle est parvenue à reconstituer les motifs de Brown, sans pouvoir savoir si le chimiste avait utilisé la même méthode.

Sarah-Marie Belcastro enseignant les mathématiques du tricot, sa passion. Elle a tricoté son poncho !

Une fois lancée l’idée générale du défi, les mathématiciens se tournent logiquement vers des surfaces plus exotiques à tricoter. Un exemple qui vient volontiers à l’esprit est celui du ruban de Möbius. Il s’agit de la surface que l’on obtient par exemple à partir d’un rectangle de papier dont on recolle les largeurs, en faisant pivoter l’une d’elle avant le recollement. La principale caractéristique de la surface ainsi constituée est qu’elle n’a qu’une seule face, contrairement à un ruban classique, qui en possède deux.

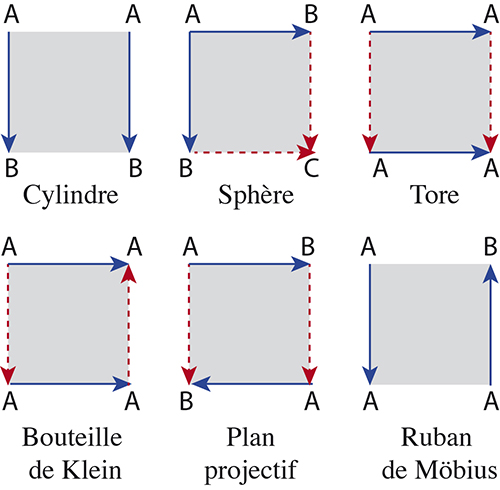
Construction de six surfaces topologiques usuelles en recollant les bords d’un rectangle.

Pour tricoter un ruban de Möbius, au lieu de joindre les côtés en fin de tricotage, Sarah-Marie Belcastro a mis au point une méthode permettant d’intégrer le demi-tour au tricotage lui-même. Avec sa technique, les aiguilles sont parallèles aux flèches doubles du rectangle de base et le tricotage suit simultanément les deux côtés à flèches simples du rectangle ; ainsi le demi-tour de torsion est-il automatiquement présent dans le tricot. Un avantage de cette méthode est que les coordonnées (abscisse et ordonnée) correspondent aux rangs et aux colonnes de la maille. Le tricoteur ajuste ensuite la courbure des surfaces à l’aide de diminution ou d’augmentation des mailles dans un rang.

Illustration de la technique de Sarah-Marie Belcastro sur la bouteille de Klein.

Autre surface célèbre entre toutes à laquelle Sarah-Marie Belcastro s’est attaquée : la bouteille de Klein. Cette surface sans bord, non orientable, n’a ni intérieur ni extérieur. Si on la découpe selon l’une de ses génératrices, on obtient deux rubans de Möbius. La bouteille de Klein est une « immersion » dans l’espace à trois dimensions, car elle se traverse selon une courbe d’auto-intersection. En clair : si vous savez tricoter un ruban de Möbius, vous pouvez confectionner une bouteille de Klein !

Inspirée par un livre de topologie algébrique d’Allen Hatcher, Sarah-Marie Belcastro a tricoté de nombreuses surfaces, notamment un tore comportant un motif correspondant au graphe complet K₇ (sept points tous reliés par des segments). Le motif est digne d’intérêt dans la mesure où, lorsque ce graphe est tracé dans le plan ordinaire, ses segments se croisent forcément (on dit que le graphe est non planaire), alors que, sur un tore, il est possible de le dessiner en évitant les intersections entre segments.

Tore incorporant K₇.

Une autre surface pertinente est celle engendrée par une tige dont la section est un Y aux bras de même longueur, la tige étant recourbée pour joindre l’une de ses deux extrémités à l’autre, après une torsion d’un tiers de tour. La surface ainsi obtenue ne comporte qu’un seul bord continu, qui équivaut à un cercle. Sarah-Marie Belcastro l’a tricoté en turban !

Le crochet hyperbolique

Les succès obtenus au tricot sont remarquables. Depuis, d’autres techniques ont essaimé. La mathématicienne lettonne Daina Taimina (portrait en page précédente), qui enseigne à l’université Cornell (New York), a ainsi lancé à la fin des années 1990 la mode du crochet hyperbolique en découvrant certains modèles en papier de plans hyperboliques réalisés par William Thurston (1946–2012). Elle a entraîné dans son sillage les mathématiciennes Elaine Ellison et Gabriele Meyer. Des expositions sont fréquemment organisées pour exhiber les plus belles réalisations topologiques en crochet hyperbolique.

Daina Taimina entourée de ses œuvres.

Les artistes ne sont pas en reste. L’artiste textile américaine Sheila Hicks, qui a fait l’objet d’une belle rétrospective en 2018 au Centre Pompidou (Paris), obtient par sa pratique à mi-chemin entre tapisserie et sculpture des surfaces magnifiques qui peuvent susciter l’intérêt des mathématiciens.

Atterrissage. Sheila Hicks, 2014, détail.

Martin Gardner avait écrit une petite nouvelle mathématique : en le tournant d’un demi-tour, un mathématicien magicien faisait disparaître une face sur les deux d’un ruban magique ; en le tournant encore d’un demi-tour, il supprimait les deux faces ! Le tricotage des surfaces complexes permet de mieux appréhender les caractéristiques topologiques de ces objets et d’en faciliter la compréhension « tactile ». C’est un outil pédagogique encore trop peu exploité.

Lighthouse in the Flatlands. Sheila Hicks, 2016, détail.

Pillar of Inquiry, supple column. Sheila Hicks, détail.