Pour fabriquer une balle de ping-pong, rien de plus simple : on colle entre eux deux hémisphères en plastique. Voilà sans doute la question qui est le plus facilement réglée. Pour la plupart des autres balles et ballons utilisés dans le sport, en revanche, la géométrie est plus élaborée. L’idée générale consiste souvent à coller des pièces sur un noyau sphérique en caoutchouc, de sorte à ce que la surface de la balle ou du ballon ait les propriétés physiques requises pour le sport considéré.

Les huit pièces du ballon de basket

Aviez-vous remarqué que la surface extérieure d’un ballon de basket se compose de huit pièces identiques ? On peut les représenter sur une surface plane à l’aide d’une projection rectangulaire.

Une telle projection est équirectangulaire, c’est-à-dire que les coordonnées polaires de latitude et de longitude sont considérées comme des coordonnées cartésiennes, les méridiens et les parallèles y sont des lignes équidistantes. Le schéma montre que les pièces extérieures du ballon de basket sont au nombre de huit, ainsi conçues. D’une part, la sphère est partagée en deux grands cercles orthogonaux. La déformation induite par la projection rectangulaire rend leur visualisation difficile ; il faut imaginer deux grands cercles tracés selon deux méridiens perpendiculaires, qui produisent les quatre pièces orange. En sus, le dessin montre une courbe qui découpe chacune de ces pièces en deux morceaux géométriquement identiques. L’équation de cette courbe implique des fonctions trigonométriques classiques.

Les courbes à la surface du ballon de basket peuvent faire penser à… la balle de tennis. Découpons à plat deux pièces de feutrine, que l’on colle sur un noyau en caoutchouc. Les deux pièces sont identiques, elles ont donc le même périmètre, ce qui permet de joindre leurs contours respectifs point par point. Toute la question est de trouver la « meilleure » forme à donner à nos deux pièces afin que celles-ci épousent au mieux la forme d’une sphère. La géométrie offre plusieurs méthodes. On peut par exemple utiliser la même courbe que pour le ballon de basket. Pour a = 0,44, on obtient le découpage suivant.

Une autre méthode consiste à « mordre » sur la sphère avec un cylindre et un parallélogramme, de la manière suivante.

On peut enfin utiliser la surface d’Enneper, du nom d’un mathématicien allemand (1830–1885). Celle-ci enveloppe les plans médiateurs de deux points situés sur deux paraboles homofocales (leurs plans sont perpendiculaires et le sommet de l’une passe par le foyer de l’autre). Avec de l’habileté, on peut matérialiser cette surface en trempant une couture de balle de tennis dans une solution savonneuse, de façon à obtenir un film de savon.

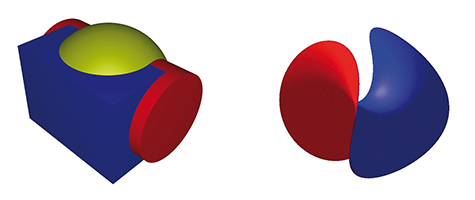
Mais le ballon le plus connu reste celui des footballeurs. Pour le fabriquer, on pourrait procéder comme pour celui utilisé au basket. Le besoin de plus de souplesse a pourtant conduit à utiliser davantage de pièces en cuir. L’idée est d’approcher la sphère par un polyèdre régulier. L’icosaèdre, à vingt faces triangulaires, remplit moins bien la sphère que le dodécaèdre, à douze faces pentagonales (60,55 % du volume, contre 66,49 %) ; il a quand même été retenu car il compte plus de faces et, surtout, ses angles sont moins saillants. De plus, après être tronqué pour procurer un supplément d’adoucissage, il remplit environ 95 % du volume de la sphère circonscrite.

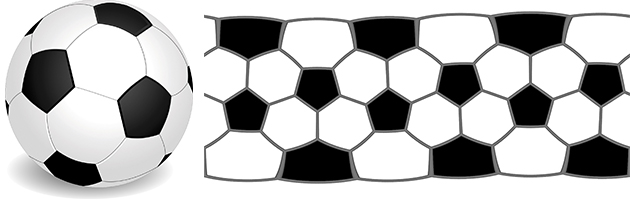
On aurait pu envisager de tronquer encore davantage pour épouser mieux la forme de la sphère. Au lieu de l’icosaèdre tronqué, on aurait alors utilisé le rhombicosidodécaèdre (soixante-deux triangles, carrés et pentagones ; soixante sommets de degré 4). Le problème, c’est que, pour un ballon de football d’environ 70 centimètres de circonférence, la longueur totale de la liaison des pièces avoisine déjà les dix-huit mètres ! Le risque au niveau des coutures explique qu’on en soit resté là, le rhombicosidodécaèdre comptant cent vingt (au lieu de quatre-vingt-dix) arêtes… et autant de coutures.

Aujourd’hui, la technologie permet de fabriquer le ballon de football avec moins de pièces, qui sont désormais en polyuréthane et non plus en cuir. Le nombre de pièces des ballons de la Coupe du monde se réduit ainsi comme peau de chagrin : 14 en 2006 (Allemagne, Teamgeist), 8 en 2010 (Afrique du Sud, Jabulani), 6 en 2014 (Brésil, Brazuca) et en 2018 (Russie, Telstar).

Cauchy et le volleyball

L’évolution du ballon de football n’est pas étonnante du point de vue géométrique. En effet, depuis longtemps, une méthode analogue est appliquée pour fabriquer le ballon de volleyball : chaque face du cube est découpée en trois rectangles identiques.

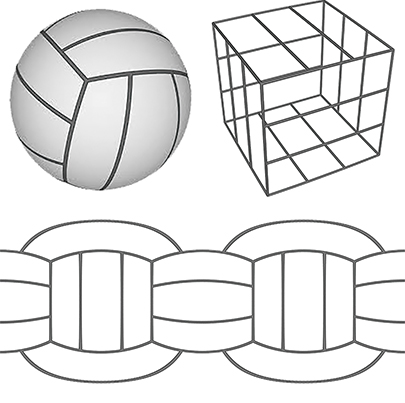
Cette construction repose en partie sur un théorème dû à Cauchy qui énonce que tout polyèdre convexe est rigide : si les faces de deux polyèdres convexes sont deux à deux isométriques, alors ces polyèdres sont isométriques. Ainsi, un patron de polyèdre convexe détermine ce polyèdre de façon unique. Par conséquent, un modèle physique d’un polyèdre convexe obtenu en reliant des faces rigides par des charnières flexibles est indéformable.

 Sans oublier le golf…

La géométrie s’invite également dans la confection des objets de plus petite taille, comme la balle de golf. Si son poids et son diamètre sont très réglementés, ce n’est pas le cas pour sa forme et, surtout, pour le nombre de ses alvéoles (de 250 à 450). Il s’agit d’optimiser portance et traînée aérodynamique, ce qui permet au golfeur d’augmenter son drive (coup joué avec le club n°1) d’une centaine de mètres ou plus par rapport à ce qu’il pourrait faire avec une balle lisse !

Comment disposer les alvéoles ? Considérons le polyèdre dont elles sont les sommets, et notons S le nombre de ses sommets, F celui de ses faces et A celui de ses arêtes. On ne peut pas utiliser que des hexagones, car les angles autour de chaque sommet totaliseraient 360° (trois hexagones jointifs en leurs sommets forment un angle de 360°), ni un polygone à davantage de côtés (heptagone…) car le polyèdre ne serait plus convexe.

Afin de « ressembler le plus possible à une sphère », on ne prend pas de carré ni de triangle : seulement des pentagones (en nombre p) et des hexagones (en nombre h). Chaque sommet du polyèdre est de degré 3 (c’est-à-dire que trois arêtes arrivent sur lui, formant entre elles des angles de 108° et de 120°). On en déduit que 3S = 5p + 6h. Par ailleurs, on a aussi F = p + h, ainsi que 2A = 5p + 6h (puisque chaque arête borde deux faces). La célèbre relation d’Euler S + F – A = 2 (voir Tangente 174, 2017) permet d’éliminer h et de montrer que p = 12 : il y a ainsi le même nombre de pentagones sur une balle de golf que sur un ballon de football classique !

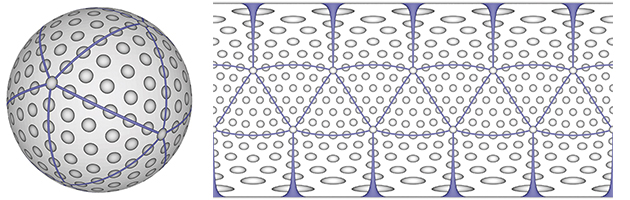
En travaillant encore un peu sur les relations précédentes, il vient aussi que S = 20 + 2h, F = 12 + h et A = 30 + 3h. Le choix qui nous rapprocherait le plus de la sphère est alors celui où chaque sommet appartient à un pentagone et à deux hexagones, les angles y totalisant 108° + 120° + 120° = 348°. On aurait alors S = 5p = 60 et h = 20 : revoilà l’icosaèdre tronqué du ballon de football classique. Plus réaliste pour une balle de golf, on peut prendre h = 171 hexagones (S = 362, F = 183, A = 543), et donc compter 362 alvéoles (vingt triangles avec chacun dix alvéoles à l’intérieur, trente arêtes – bleues – avec chacune cinq alvéoles en dehors des extrémités, douze alvéoles aux sommets des pentagones).