Dans l’introduction de son Traité des épicycloïdes et de leur usage dans les méchaniques daté de 1694, Philippe de La Hire résume bien la situation des engrenages en cette fin de XVII ^e siècle : « Comme personne ne se préoccupe de la forme à donner aux dents des engrenages et que celle-ci est abandonnée aux bons soins de l’ouvrier qui la réalise, la plupart des mécanismes ne marchent tout bonnement pas ! » Dans son traité, il propose une solution : donner aux profils des dents une forme de cycloïde. Est-il le premier à y penser ? Dans cette même introduction, il explique qu’il a eu l’occasion de refaire au château de Beaulieu (Essonne) la roue d’une pompe utilisant ce profil de cycloïde et que la paternité de cette roue revenait à l’« excellent géomètre » Girard Desargues. Celui-ci n’ayant laissé aucun écrit sur le sujet, il était certainement arrivé à ce profil par tâtonnements…

De gauche à droite : Philippe de La Hire (1640–1718). Gottfried Wilhelm Leibniz (1646–1716). Ole Christensen Roemer (1644–1710).

Enquête sur une pompe à eau

Quelques décennies plus tôt, l’ingénieur Sébastien Pontault (1612–1674) avait commandé à Girard Desargues, pour son château de Beaulieu, lieu-dit situé aujourd’hui sur la commune de Marolles-en-Hurepoix, la construction d’une pompe particulièrement performante. Le chantier a eu lieu après 1626, date de la venue de Desargues à Paris. Le château serait devenu la propriété de l’homme de lettres Charles Perrault, qui possédait une autre maison de campagne à Viry (aujourd’hui Viry-Châtillon, également dans l’Essonne). Viry est approximativement située à mi-chemin entre Paris et Marolles-en-Hurepoix.

La pompe fit l’admiration du mathématicien, astronome et physicien néerlandais Christiaan Huygens (1629–1695) lors de sa visite de 1671 à son ami Charles Perrault. Lorsque la roue de la pompe ne fut plus en état de fonctionner, l’astronome et physicien Adrien Auzout (1622–1691) ainsi que l’abbé Edme Mariotte (1620–1684), par ailleurs physicien et botaniste, auraient demandé à La Hire de la restaurer. Ce que fit ce dernier. La Hire aurait-il alors eu accès à des documents de Desargues à cette époque ? Il s’en défend. Mais Desargues était aussi un familier du père de La Hire, le peintre Laurent de La Hire (1606–1656). L’auteur du Traité des épicycloïdes aurait-il eu des informations par ce biais ? Il prétend qu’il a eu l’idée d’utiliser des cycloïdes vingt ans plus tôt, et qu’il en avait parlé à Adrien Auzout, à Edme Mariotte et au géodésien et astronome Jean-Félix Picard (1620–1682). Malheureusement, au moment de la parution du traité, ces trois témoins sont décédés !

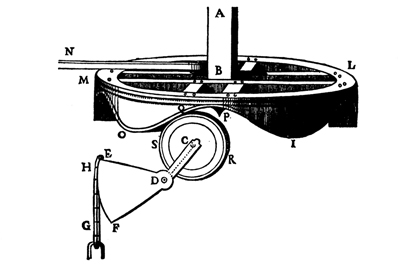Schéma de la pompe de Desargues au château de Beaulieu. 

La cycloïde est une courbe qui va être intensément étudiée, on l’a même surnommée l’Hélène des mathématiciens ! Elle ne semble pas avoir été mise au jour dans l’Antiquité, même si certains astronomes utilisèrent les épicycles pour modéliser les mouvements des planètes… L’un des premiers à s’intéresser à elle est Blaise Pascal (1623–1662), puis Galilée. Le sujet regagne en intérêt avec le père Marin Mersenne (1588–1648), lorsqu’il lance le défi de calculer l’aire sous une arche de cycloïde. Le mathématicien et physicien Gilles Personne de Roberval (1602–1675) montre en 1635 que l’aire d’une arche est trois fois l’aire du cercle générateur. Sir Christopher Wren (1632–1723), architecte de son état, montre que la longueur d’une arche est huit fois le rayon du cercle générateur.

La cycloïde matérialise la trajectoire d’un point situé sur un cercle qui roule sans glisser sur une droite fixe.

L’astronome danois Ole Roemer conseille à Huygens de s’intéresser à la cycloïde ; ce dernier essaiera sans succès de l’utiliser pour fabriquer des pendules isochrones. Roemer arrive à Paris en 1671 d’Uraniborg, le fameux observatoire de Tycho Brahé situé sur l’île de Ven (Danemark). Il est ramené, semble-t-il, par Philipe de La Hire.

Roemer fera une communication en 1676 à l’Académie des sciences sur l’utilisation des cycloïdes pour le profil des dents ; il n’existe malheureusement pas de document relatif à cette communication. Six années plus tard, La Hire reprend le poste de Roemer à l’observatoire de Paris, le Danois étant rappelé au pays. Ainsi, le Français a nécessairement entendu parler des travaux de son confrère sur le sujet.

Leibniz était lui aussi dans la capitale au moment de la communication de Roemer (il est à Paris en 1674, et au moins épisodiquement les deux années suivantes). Or, La Hire ne cite jamais le nom de Roemer dans son traité, d’où la dispute…

Des dents qui grincent…

Le mathématicien et homme politique Nicolas de Condorcet (1743–1794), dans son éloge, nous informe lui aussi de la trouvaille de Roemer.

En 1698, dans une lettre au mathématicien et physicien suisse Jean Bernoulli, Leibniz s’étonne de trouver dans le traité de La Hire des matériaux issus de ses propres travaux ; il pense que le Français a mis la main sur des papiers de Mariotte, à qui Leibniz avait fait des communications orales. Il poursuit : « Je n’approuve pas que les doctes taisent le nom de ceux dont ils tirent profit. » Il se rappelle qu’il avait été instruit à Paris par Roemer, mais aussi par Huygens, de l’utilisation des cycloïdes. On dispose encore de six lettres de Leibniz à Roemer, dans lesquelles il presse ce dernier de publier sur les engrenages et de revendiquer la découverte. Cependant, dans ses réponses, le Danois reste muet sur ce sujet.

La fin du XVII ^e siècle voit la naissance d’un nouvel outil mathématique : le calcul infinitésimal. Aujourd’hui, on peut peut-être dire, d’une certaine manière, que la controverse entre Leibniz et Newton était vaine puisque les deux savants sont parvenus aux résultats que nous connaissons par des voies différentes, mais à l’époque la première dispute est l’adoption ou pas du calcul infinitésimal. Grâce à cette théorie, de nouveaux résultats spectaculaires sont obtenus, comme par exemple la détermination de la courbe brachistochrone étudiée par Leibniz, Jean et Jacques Bernoulli. Mais une opposition se crée. En 1697, La Hire présente un mémoire, Remarque sur l’usage qu’on doit faire de quelques suppositions dans la méthode des infinis petits, ce qui lui vaut d’être rangé par son compatriote Pierre Varignon (1654–1722) comme un mathématicien « de vieux stile ».

La dispute entre Leibniz et La Hire semble donc plus être une controverse autour du calcul infinitésimal qu’autour de la postérité de Roemer, comme paraît en attester un courrier de Jean Bernoulli adressé au philosophe et mathématicien allemand : « Je me demandais aussi quel génie avait conduit cet homme [La Hire], ignorant à peu près de tout notre calcul et de toutes les nouvelles méthodes, à la connaissance de ces figures. Mais depuis que vous m’avez appris que Roemer en est l’inventeur, je ne m’étonne plus. » D’ailleurs Leibniz se radoucit en 1698 dans une lettre, comprenant que La Hire commence à utiliser les infiniment petits. 

Les disputes semblaient assez courantes, puisqu’une autre querelle scientifique opposa La Hire (!) et le mathématicien et physicien allemand Ehrenfried Walter von Tschirnhaus (1651–1708) au sujet des caustiques. La construction de Tschirnhaus fut montrée fausse par La Hire, puis par Jean Bernoulli ; Tschirnhaus corrigea son erreur en 1690.

Le funeste destin de la cycloïde

L’ironie de l’histoire est que les planètes ne parcourent aucunement des cycloïdes. L’utilisation de ces courbes s’est révélée inopérante dans les pendules, au grand dam de Huygens, car la réalisation d’une cycloïde parfaite est délicate (voir Un monde d’oscillations, Tangente 179, 2017). De même, pour les engrenages, l’industrie mécanique adoptera pour des raisons pratiques des profils de dentures en forme de développantes de cercles. Aujourd’hui, seule l’industrie horlogère a conservé les cycloïdes. Funeste destin que celui de l’Hélène des mathématiques, tombée dans l’oubli de la mécanique…

Il faudra attendre le XVIII ^e siècle pour que l’histoire des engrenages se poursuive. Ils deviendront l’objet technologique par excellence, omniprésent dans nos vies et symbole de l’industrie.