Les mesures astronomiques de Tycho Brahe (1546–1601), très précises pour l’époque, furent interprétées par Johannes Kepler (1571–1630), qui en induisit ses lois du mouvement des planètes autour du soleil. Pour cela, il utilisa des ellipses, des courbes connues depuis l’Antiquité comme intersection d’un cône et d’un plan.

Des parterres de fleurs dans l’espace

Pour décrire la première loi de Kepler, on exploite une propriété des ellipses, qui par ailleurs les rend faciles à dessiner. Dans un domaine très différent, ce sont les courbes idéales pour former des parterres de fleurs : esthétiques et faciles à construire ! Pour cela, il faut trois piquets et une corde. On plante deux piquets et on y attache la corde, qui doit rester molle. On prend alors l’autre piquet en main et on tend la corde. La courbe décrite par ce piquet mobile quand on tourne autour des deux piquets fixes est une ellipse, dont les foyers sont ces piquets. Un cercle est donc une ellipse dont les deux foyers sont confondus.

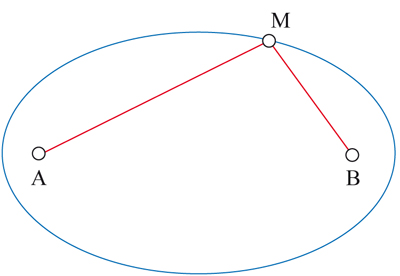Une ellipse de foyers A et B : ensemble des points M tels que AM + MB est constant.

On peut alors énoncer la première loi de Kepler : les trajectoires des planètes sont des ellipses dont le Soleil occupe l’un des foyers. Les deux autres lois fournissent la vitesse de la planète et sa période. Kepler avait donc trouvé une description assez explicite du mouvement des planètes. On aurait pu penser d’ailleurs que le côté elliptique n’était qu’approximatif.

L’explication de la nature de ces trajectoires vint d’Isaac Newton (1643–1727) en utilisant la méthode qu’il a exposée dans la Méthode des fluxions, et des suites infinies, ouvrage traduit en français par Buffon. Tout d’abord, Newton appelle fluente une grandeur variable dans le temps. La fluxion d’une fluente x est alors sa vitesse. En termes modernes, il s’agit de sa dérivée par rapport au temps t. La notation de Newton de la fluxion de x, toujours utilisée par les physiciens, consiste à surmonter x d’un point. Il donne alors les principales règles que nous connaissons concernant la fluxion d’une somme, d’un produit… Le lien avec le calcul différentiel de Leibniz est simple puisque \( {\rm d}x=\dot{x}{\rm d}t\)  . Les deux calculs de Newton et de Leibniz sont équivalents. Si l’on en croit sa parole, Newton a l’antériorité de la découverte. Cependant, comme Leibniz publia sa méthode avant lui, elle est souvent attribuée à ce dernier. L’explication donnée par Newton était qu’il ne voulait pas publier sa définition des fluxions car elle manquait de rigueur. Voici ce qu’il écrit à ce sujet : « Les rapports ultimes dans lesquels les quantités disparaissent ne sont pas réellement des rapports de quantités ultimes, mais les limites vers lesquelles les rapports de quantités, décroissant sans limite, s’approchent toujours, et vers lesquelles ils peuvent s’approcher aussi près qu’on veut. » Pour comprendre la difficulté, il faut penser que la notion de limite ne sera précisée qu’un siècle après la mort de Newton. En fait, Leibniz comme Newton ont apporté leurs pierres à l’édifice. À travers ses fluxions, Newton est l’inventeur de la notion de dérivée, alors que Leibniz est celui de différentielle. Les deux se complètent, même si la notation différentielle est plus commode. Avec son utilisation de la mécanique à travers la notion de vitesse, la théorie des fluxions est autant un apport de la physique aux mathématiques qu’un apport des mathématiques à la physique. Jean Le Rond d’Alembert (1717–1783) dégagea cette notion de dérivée de l’idée de vitesse mais en se reposant sur la notion de limite, tout aussi mal définie. Il faudra attendre Augustin-Louis Cauchy (1789–1857) pour supprimer ce recours à l’intuition.

Les trajectoires sont coniques

Cette méthode des fluxions permit de retrouver la trajectoire elliptique des planètes à partir des lois fondamentales de la mécanique newtonienne, en particulier celle qui lie les forces exercées sur un corps et son accélération, et celle de l’attraction universelle, que Newton expose dans ses Principes mathématiques de la philosophie naturelle, traduits en français par Émilie du Châtelet. À travers ces lois, si on se limite à deux corps (le soleil et une seule planète), le problème se ramène à une équation différentielle du second ordre, que Newton sut résoudre grâce à la géométrie (voir article "La méthode synthétique de Newton"). Il retrouva ainsi les résultats de Kepler à partir de la loi de l’attraction universelle… et découvrit en plus d’autres solutions. Certains objets célestes peuvent avoir des trajectoires hyperboliques ou paraboliques, mais toutes sont coniques !

La théorie de Newton fut un succès car, pour la première fois, on pouvait faire des prévisions fiables sur les mouvements des corps. Cependant, la nature de la force d’attraction avait un côté mystérieux, presque mystique. Comment s’effectuait cette « attraction à distance » ?

Pour l’expliquer, en 1916, Albert Einstein prédit l’existence d’ondes gravitationnelles se propageant à la vitesse de la lumière. On les chercha longtemps, pour finir par les trouver en 2016 dans la fusion de deux trous noirs, plus de trois siècles après Newton.

Suite à la réussite du savant britannique, on découvrit que la plupart des phénomènes physiques étaient régis par des équations différentielles. En ce qui concerne la mécanique, les lois de Newton fournissent des équations de la forme   \( \ddot{x}=f(x,\dot{x},{\rm t})\)  ,
qui expriment que l’accélération est fonction de la position, de la vitesse et du temps, avec des conditions portant sur la position x et la vitesse  \( \dot x\)  à l’instant initial. La question se scinde alors en deux. Tout d’abord elle a un côté qualitatif : existence et unicité de la solution, stabilité, forme des trajectoires… La question a également un côté quantitatif permettant de dessiner les solutions. Il est rare que, pour cela, on trouve des solutions exactes comme dans le cas du problème des deux corps (celui du Soleil et d’une planète par exemple). Dès qu’on en introduit un troisième, on doit avoir recours à des méthodes numériques, la plus simple étant due à Leonhard Euler. 

Dans le cas d’une équation de la forme  \( \dot x = f(x,t)\)   avec la condition x (0) = x₀, la méthode d’Euler consiste à calculer x (Δ t), pour une valeur de Δ t « petite », en utilisant l’approximation  \( x(\Delta t)\simeq x(0)+\dot x (0)\Delta t\)  qui vient de la définition de la dérivée en 0 comme limite du rapport [x (Δ t) – x (0)] / Δ t quand Δ t tend vers 0. On obtient ainsi une approximation de x (Δ t) ; on recommence pour obtenir x(2 Δ t), et ainsi de suite. Le même principe peut être amélioré pour obtenir une meilleure approximation.

Les mathématiques permettent donc de calculer les positions des planètes avec précision et, de même, de faire des prévisions dans le domaine de la physique. Cela peut surprendre ! À la fin du XX ^e siècle, le mathématicien et philosophe Gilles Châtelet l’exprime ainsi : « Comment se fait-il que la mathématique, qui dans les sciences est à la fois la bonne à tout faire et la reine des sciences, soit si utile dans cette cuisine malpropre qu’est la physique ? » Cette interrogation a fait l’objet d’un article célèbre du physicien Eugene Wigner, en 1960. Il est intitulé la Déraisonnable Efficacité des mathématiques dans les sciences de la nature. Wigner y qualifiait cette efficacité de « miracle » ou de « don magnifique que nous ne comprenons ni ne méritons », comme si ses raisons profondes étaient situées au-delà des limites de notre compréhension du monde. Sans doute les raisons de cette efficacité ne doivent pas être cherchées dans un miracle mais plutôt dans le fait que les axiomes des mathématiques cherchent à « coller à la réalité ». De plus, les mathématiques sont faites pour détecter des invariants, le groupe ou la structure cachés dans une théorie. C’est ce qui importe en physique.

Statue d’Isaac Newton, 
Conçu par Louis-François Roubiliac en 1775,
Trinity College Chapel, Cambridge, Angleterre.