Hérodote attribue l’origine de la géométrie au partage de terres gagnées sur des marais, drainés et canalisés sous le règne du pharaon Sésostris II. La géométrie est alors entendue sous son sens étymologique d’arpentage, les connaissances acquises n’étant qu’empiriques. Il faut attendre le génie grec pour que des démonstrations soient établies. Au début du VI ^e siècle avant notre ère, Thalès de Milet avait échoué à appliquer ses techniques mathématiques sur une figure non rectiligne. Au siècle suivant, dit siècle de Périclès, l’orateur Antiphon considérait le cercle comme un polygone régulier d’une infinité de côtés. Cette vision de l’infini était trop en avance sur son temps et n’eut pas d’écho.

Un infini implicite

Par principe, les Grecs excluaient l’infini car il ne peut « entrer » dans aucun raisonnement. Cette notion se limitait à la simple possibilité de poursuivre un processus opératoire pouvant être itéré sans limitation. C’est ainsi qu’Hippias d’Élis établit vers –430 la méthode de construction de la quadratrice, dite de Dinostrate, en un nombre infini d’étapes. L’idée d’Antiphon fut néanmoins reprise par Euclide, qui encadra le cercle par des polygones réguliers circonscrits et inscrits au cercle et en déduisit que l’aire du cercle est proportionnelle au carré de son diamètre.

Astronomes et physiciens, confrontés à la matérialité, ont pu être les premiers à imaginer la notion d’infiniment petits. Zénon d’Elée envisage une divisibilité indéfinie des corps, alors que des astronomes font des approximations en négligeant certaines quantités. Ainsi, Aristarque de Samos, le premier hélio-centriste selon Archimède, considère les rayons du soleil comme parallèles quand il modélise la séparation ombre / lumière sur la lune par un grand cercle. En mathématiques, on peut estimer la théorie des incommensurables de Pythagore, étudiée par Démocrite, comme une introduction de cette notion. L’école de Platon a bien développé la construction de tangentes, mais qui ne s’applique qu’aux coniques, et encore grâce aux propriétés particulières de leurs diamètres (voir FOCUS "Les diamètres des coniques"). Pour Aristote, l’infini ne peut être qu’en puissance (le concept d’infini ne peut être pensé que comme un possible) et non en acte (à savoir, un objet mathématique à part entière, qui pourra être manipulé, sur lequel on pourra effectuer des calculs arithmétiques…) et est synonyme d’inachevé. Il faut en fait attendre Eudoxe de Cnide au IV ^e siècle avant notre ère pour une avancée significative avec la méthode d’exhaustion, terme qui implique de tout prendre en compte, jusqu’à la plus petite partie. Le premier texte connu qui utilise cette méthode est le douzième livre des Éléments d’Euclide.

La méthode d’exhaustion

En langage moderne, cette méthode repose sur le principe suivant :

(I) Si deux quantités variables q et Q restent toujours proportionnelles en tendant vers deux limites l et L, alors ces limites sont dans la même proportion : 

  \( \dfrac{\text {Q}} {q} = \dfrac{\text L} {l}.\)

Deux lemmes sont encore nécessaires :

(II) Si l’on ajoute un certain nombre de fois une grandeur g > 0 à elle-même, le résultat finira par dépasser une quantité A donnée, si grande qu’on la suppose.

C’est une caractéristique dite archimédienne qu’Archimède de Syracuse lui-même signale comme d’un grand usage chez ses devanciers.

(III) Si d’une grandeur g > 0 quelconque on retire la moitié ou plus de sa moitié, du reste, sa moitié ou plus de sa moitié, et ainsi de suite un certain nombre de fois, le reste sera plus petit qu’une quantité donnée, si petite qu’on la suppose.

La méthode d’exhaustion permet de démontrer par exemple que « deux cercles sont entre eux comme les carrés de leurs diamètres ».

Dans un premier temps, Euclide démontre (ce que l’on supposera acquis) que « deux polygones inscriptibles ont leur surface dans le même rapport que le carré des rayons de leur cercle circonscrit », ce qui revient à dire que deux polygones ont leur surface proportionnelle au carré d’une de leurs dimensions caractéristiques. Cette proposition permet au passage l’une des plus belles démonstrations du théorème de Pythagore (voir FOCUS "Pythagore minimaliste").

Considérons deux cercles avec un carré inscrit. Ces carrés seront, en surface, dans le même rapport que les polygones réguliers de huit, seize… côtés, obtenus par doublement du nombre de côtés, à savoir le rapport du carré des diamètres correspondant. Mais, à chaque duplication, on retranche plus de la moitié de l’espace compris entre la circonférence et le dernier polygone (voir ci-dessous). En effet, le triangle BON, ajouté à la surface du polygone par duplication, est en surface la moitié du rectangle BIEN, lui-même strictement supérieur au « segment de cercle » BON. Par conséquent, l’excès de chaque cercle sur les polygones inscrits diminue de plus de la moitié à chaque duplication et, d’après (III), peut devenir plus petit qu’aucune surface donnée. Le théorème d’Eudoxe (I) s’applique donc et les deux cercles sont bien dans le rapport annoncé.

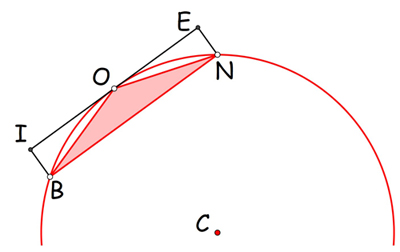Méthode d’exhaustion sur le cercle.

Cette démonstration fait partie de celles qu’Adrien-Marie Legendre (1752–1833) a désiré conserver dans ses propres Éléments de géométrie, évitant ainsi les dangereuses « évidences » d’un passage à la limite.

Archimède, l’esprit supérieur

Archimède a reformulé la méthode d’exhaustion, qu’il applique principalement à la mesure de la sphère. Très fier, à juste titre, de la relation entre la sphère et le cylindre (« La surface d’une sphère vaut les deux tiers de celle du cylindre circonscrit, et son volume également les deux tiers de celui du même cylindre »), il demanda que la figure d’une sphère inscrite dans un cylindre fût gravée sur son tombeau. C’est ce qui permit à Cicéron, près de cent cinquante ans plus tard, de le retrouver : « Voilà que mes yeux tombent sur une petite colonne qui émergeait à peine des buissons : elle était surmontée d’une sphère et d’un cylindre. »

Le Syracusain utilise en outre les principes suivants :

(IV) La ligne droite est le plus court chemin d’un point à un autre. De deux lignes planes concaves du même côté, ayant mêmes extrémités et l’une étant comprise entre l’autre et la corde commune, la première est plus courte que l’autre.

Il a appliqué la même méthode aux coniques. Voici sa démonstration pour le cercle. 

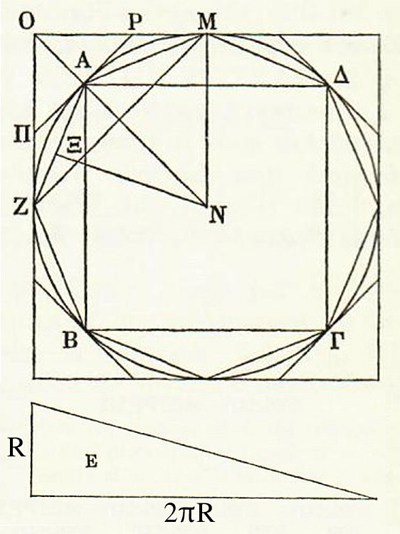
« Tout cercle est équivalent à un triangle rectangle (E) dans lequel l’un des côtés de l’angle droit est égal au rayon du cercle et la base égale au périmètre du cercle. » Supposons le cercle d’aire strictement plus grande que celle de (E) et inscrivons, par duplication, des polygones réguliers de quatre, huit… côtés jusqu’à ce que l’excès du cercle sur le polygone soit plus petit que celui du cercle sur (E). Le polygone est alors plus grand que (E), ce qui ne se peut. Il est en effet constitué de triangles identiques ayant pour hauteur l’apothème NΞ, inférieure au rayon, la hauteur de (E), et dont la somme des bases, sa circonférence, est inférieure à la circonférence du cercle, la base de (E), d’après (IV).

On suppose maintenant le cercle strictement plus petit que (E) et on considère des polygones circonscrits. On duplique de même pour obtenir un polygone de surface strictement nférieure à (E), ce qui est impossible puisque si l’apothème NA est égal au rayon du cercle, sa circonférence est supérieure à celle du cercle. Nous sommes en présence d’un magnifique double raisonnement apagogique (ou par l’absurde), dont la conclusion est que les surfaces… sont égales. 

Archimède utilise une seconde méthode, appelée par échelons, pour mesurer les volumes, conoïdes et sphéroïdes, mais pas les surfaces. Il s’agit de couper le volume à mesurer par des plans parallèles et équidistants et de construire à partir des sections de ces coupes des prismes inscrits et circonscrits. Si la première méthode n’est en somme qu’un théorème sur les limites, cette seconde méthode conduit à la représentation cartésienne d’une fonction continue avec abscisses et ordonnées et est à l’origine immédiate du calcul intégral.

Après Archimède, seul Pappus, qui énonça les théorèmes que Paul Guldin n’a pas démontrés, s’occupe de la géométrie de la mesure, en faisant un premier pas vers une simplification de la méthode d’exhaustion, appelée des indivisibles. L’infini mathématique avait pris consistance, en réaction à la scholastique et à l’autorité d’Aristote dans les écrits d’Oresme quand Kepler initia cette méthode des indivisibles qui séduisit au XVII ^e siècle Bonaventura Cavalieri, René Descartes et Blaise Pascal.

Cette théorie des indivisibles a permis de calculer rapidement des aires, mais n’a pas de fondement théorique rigoureux et, appliquée sans précautions, peut donner des résultats faux. Cependant, on peut la considérer comme ancêtre du calcul intégral. Mais c’est une autre histoire, qui vous est contée dans le Calcul intégral, Bibliothèque Tangente 50, 2014.