Gauss et l’optique géométrique

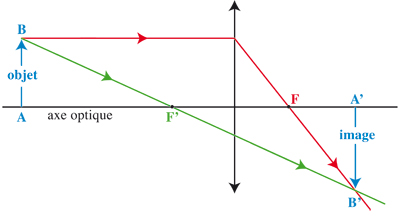
Gauss est connu des mathématiciens comme… mathématicien. Mais nombre de ses recherches couvraient le champ de la physique. On lui doit des découvertes significatives en électricité (loi de Kirchhoff), en optique et en électromagnétisme (équations de Maxwell). Ses travaux en optique reposent sur ce qui est aujourd’hui identifié comme l’approximation de Gauss. En gros, il s’agit de considérer les lentilles sphériques comme des objets sans épaisseur, représentés comme des segments de droite dont on construit la médiatrice : l’axe optique. On se limite aux rayons « peu inclinés et peu éloignés » de cet axe. On suppose que les lentilles sont stigmatiques (l’image d’un point est un point) et aplanétiques (l’image d’un objet perpendiculaire à l’axe optique est perpendiculaire à l’axe optique). Alors pour construire l’image d’un point P il suffit de considérer deux rayons issus de P ; tous les autres issus de P passeront par le point image. Cette approximation en apparence grossière est en fait souvent applicable en pratique et simplifie grandement les relations mathématiques de l’optique géométrique.

Choix du modèle, méthode de résolution…

Le réel est complexe… Pour le gérer, il faut synthétiser des ensembles d’observations cohérentes en lois, qui prennent souvent la forme de relations mathématiques. Ces lois ne décrivent que des approximations plus ou moins fines de la réalité observée. Ainsi, la trajectoire d’une planète relativement au soleil peut s’exprimer dans le cadre du problème des deux corps (ou des n corps) ou dans celui de la relativité générale, qui seule rend compte de l’avance du périhélie de Mercure. Face à un problème physique « réel », la première démarche consiste à poser des hypothèses, qui conduisent à la mise en place d’un modèle mathématique intégrant des niveaux plus ou moins sophistiqués de lois physiques. Il est rare que ce modèle permette des solutions analytiques exactes : le traitement des équations différentielles nécessite souvent un processus de discrétisation et l’usage de méthodes approchées d’analyse numérique. Les résultats obtenus doivent donc être comparés aux observations pour valider, ou non, à la fois le modèle et les méthodes numériques retenues. Les approximations sont donc indispensables en physique ! Elles concernent tantôt le choix d’un modèle, tantôt les méthodes numériques de résolution. Ce qui est extraordinaire, c’est que malgré ces différentes approximations les résultats obtenus soient souvent aussi satisfaisants !

Gaz parfaits : l’approximation de Maxwell–Boltzmann

La théorie des « gaz parfaits », décrivant le comportement de gaz à basse pression, fut développée dès les XVII^e et XVIII^e siècles, donnant naissance aux lois de Boyle–Mariotte et d’Avogadro. Elle est « presque » vérifiée expérimentalement, quelle que soit la nature chimique du gaz. Cette constatation cadre avec les théories les plus modernes : c’est l’approximation de Maxwell–Boltzmann. Dans des conditions ordinaires (température de 273°K et pression d’une atmosphère), les lois des gaz moléculaires ne dépendent pas de la nature des particules, qui se subdivisent en deux catégories déterminées à partir de leur spin, une de leurs propriétés (au même titre que la masse ou la charge électrique). On distingue d’une part les fermions, aux spins de valeur demi-entière (électrons, protons, neutrons), et d’autre part les bosons (photons ou bosons de Higgs), de spin entier ou nul. Les fermions sont soumis au principe d’exclusion de Pauli (deux fermions identiques ne peuvent être dans le même état quantique, c’est-à-dire décrit par une distribution de probabilité) alors que deux bosons peuvent occuper le même état. Cette différence entre fermions et bosons peut être négligée à haute température et basse pression, la probabilité que deux particules occupent le même état étant négligeable. Le principe de Pauli se trouve alors toujours respecté. Dans ces conditions classiques, les deux comportements tendent vers un comportement limite commun décrit par l’approximation de Maxwell–Boltzmann : la fonction de partition (grandeur englobant température, volume, énergie totale, entropie, énergie libre ou pression) d’un ensemble de N particules peut être modélisée par une fonction de N et de la fonction de partition d’une simple particule.