Attention, ce texte nécessite d'avoir lu l'article dand lequel signature et poids des pavages sont introduits.

Pour énumérer les frises du plan, nous allons commencer par… un petit détour dans l'espace, sur le cylindre ! Imaginez que vous enrouliez votre ruban, votre frise préférée, sur un cylindre. Depuis la plus haute Antiquité, les poteries et autres amphores ne sont-elles pas décorées sur leur pourtour avec de charmants motifs ? On y observe une symétrie de rotation, d'axe celui du cylindre, qui permet la duplication d'un motif tout autour de l'objet. Pour passer du cylindre au plan, il suffit de faire tendre le rayon de ce cylindre vers l'infini.

Un peu de combinatoire

Une frise de signature 33.

Une frise de signature 3x.

Le théorème du pavage, appliqué aux frises, affirme qu'une frise possède une signature comprenant un symbole infini et dont le poids total fait 2. Attention cependant à ne pas confondre le symbole 3 (de poids 1) correspondant aux rotations avec celui (de poids 1/2 et coloré en rouge) correspondant aux réflexions. En partant de 3, il ne nous reste plus qu'un poids de 1 à trouver. On trouve ainsi naturellement la signature 33. Pour comprendre complètement cette notation, pensez au même motif dessiné sur la circonférence d'une sphère : un axe de rotation traverserait le pôle Nord et le pôle Sud. Le motif vu du pôle Nord est différent du motif vu du pôle Sud, il y a bien deux centres de rotation différents. Si le diamètre de la sphère tend vers l'infini, il faut faire une infinité de rotations, d'où le choix de la notation.

On trouve tout aussi facilement la signature 3x . Dans ce cas, il n'y a qu'un seul axe de rotation à l'infini. Le motif est le même si l'on retourne la figure. Par contre, on peut passer d'une figure « à droite » à une figure « à gauche » sans traverser de miroir, d'où le miracle x .

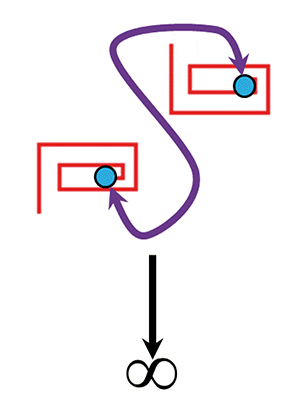Deux éléments de la frise 3x.

En consultant le tableau des poids, on se persuade très vite que la signature 3* convient également. Pour cette frise, nous avons un miroir * et un seul centre de rotation à l'infini. La figure est identique si on la retourne.

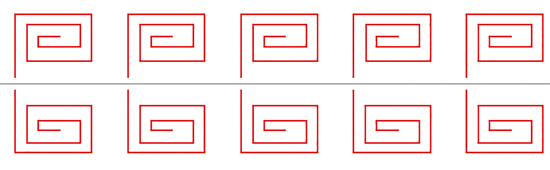
Une frise de signature 3*.

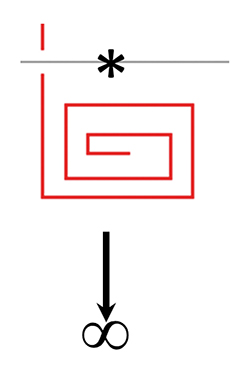
Un élément de la frise 3*.

De même, pour la frise de signature 223, on observe deux sortes de centre de rotation d'ordre 2 et un centre de rotation à l'infini. La figure est identique si on la retourne.

Cela épuise les possibilités avec 3. Passons au symbole 3 correspondant aux réflexions.

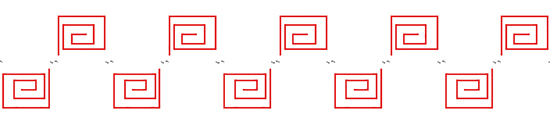
Une frise de signature 3.

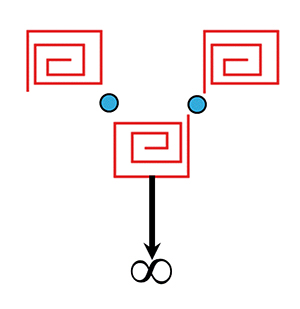
Trois éléments de la frise 3.

À la réflexion…

Le poids du symbole 3 étant de 1/2 et le poids de * étant de 1, il ne reste plus qu'à trouver un poids (ou un ensemble de poids) de 1/2 pour compléter la signature. On peut commencer par *33 . À l'infini, dans une direction perpendiculaire à la frise se coupent une infinité de miroirs (d'où le premier symbole 3 ). Mais dans l'autre direction on a aussi une autre intersection d'une infinité de miroirs, d'où le second symbole. La figure n'est pas la même si on la retourne.

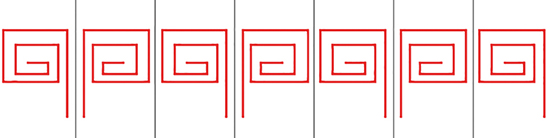
Une frise de signature *33 .

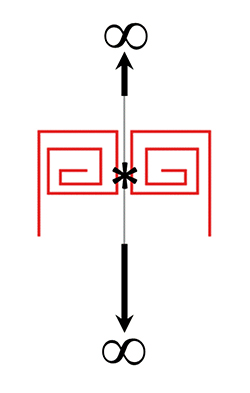
Deux éléments de la frise *33 .

Enfin, on trouve la frise *223 (qui possède deux types de croisements de deux miroirs et un seul croisement à l'infini, puisque si on retourne la frise elle est inchangée) et la frise de signature 2*3 (avec un type de centre de rotation d'ordre 2 et un croisement à l'infini ; la figure reste la même si on la retourne).

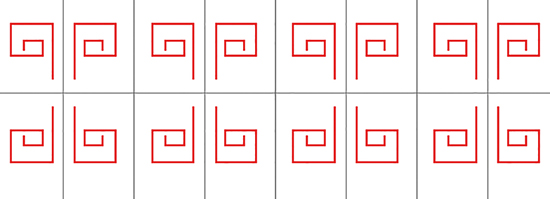
Une frise de signature *223.

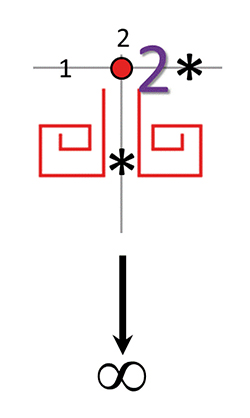
Deux éléments de la frise *223.

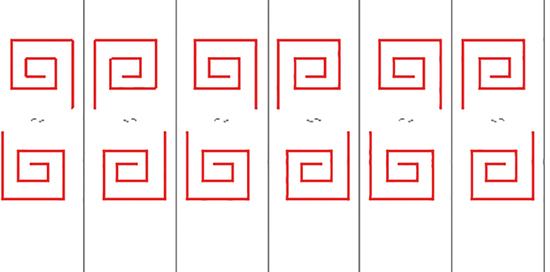
Une frise de signature 2*3 .

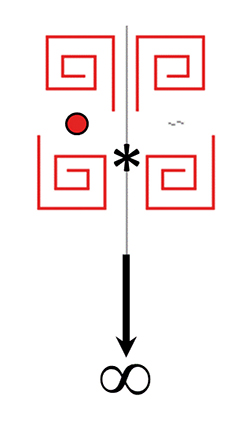
Deux éléments de la frise 2*3 .

Voilà qui termine l'inventaire exhaustif des sept frises ! Vous aurez beau vous creuser la tête, tous les motifs que vous pourrez construire pour votre salon s'y ramèneront nécessairement.