Les rep-tuiles et le Sphinx

Les rep-tuiles (rep-tiles pour les Anglo-Saxons) sont des figures pouvant se décomposer en un assemblage de n exemplaires d'une même pièce pour un certain entier n (on dit alors qu'une telle figure est rep-n), chaque pièce étant semblable à la figure de départ. Ces figures ont été étudiées par le mathématicien Solomon Golomb, connu pour sa redécouverte des polyminos. L'une des rep-tuiles les plus connues est le Sphinx.

Deux figures rep-2. En divisant à nouveau chaque pièce, on peut fabriquer des figures rep-4, puis rep-8, rep-16…

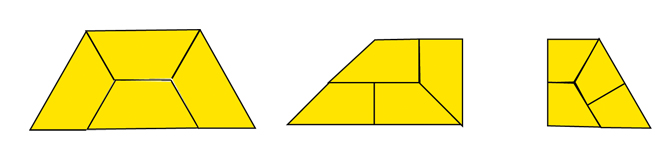Trois figures rep-4, qui permettent de construire des figures rep-16, rep-64…

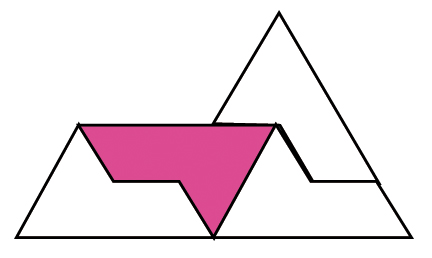 La figure du Sphinx

Défis avec les polyminos

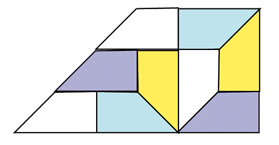Une autre facette de la question est l'étude du « rep-ordre » des polyminos. Le problème peut s'énoncer ainsi : étant donné un polymino (voir en page 8), est-il possible de reproduire un agrandissement de ce polymino en utilisant m exemplaires de ce polymino (et, dans l'affirmative, quel est le plus petit nombre m d'exemplaires dudit polymino le permettant) ?

L'existence d'une réplication d'un polymino donné découle de l'existence d'un pavage de rectangle à l'aide d'exemplaires de ce polymino. En effet, si un rectangle est pavable à l'aide d'un polymino, on peut alors paver un carré avec ce polymino ; par conséquent, on peut reconstituer un assemblage de tels carrés ayant la forme du polymino souhaité.

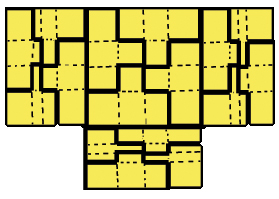Seize exemplaires du quadramino T permettent de réaliser un quadramino T quatre fois plus grand.