Souvent ornés de segments qui s'alignent merveilleusement, les pavages de l'art islamique, généralement non répétitifs (le mathématicien dira non-périodiques), semblent relever d'une magie géométrique. Prolongeant les travaux du Britannique Roger Penrose sur les pavages non-périodiques, deux physiciens américains, Peter James Lu, de l'université de Harvard, et Paul Steinhardt, de l'Université de Princeton, on montré qu'en fait ces pavages que nous admirons tant sont engendrés par cinq polygones simples dont les côtés ont tous même longueur : les tuiles de girih. 

Des tuiles pas comme les autres

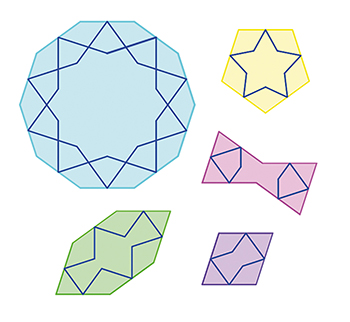
Les cinq tuiles de girih.

C'est en visitant, en 2005, une madrasa (école religieuse) du XV^e siècle à Bukhara en Ouzbékistan que Peter Lu, alors étudiant à l'université de Harvard, est attiré par les dessins aux contours complexes de sa décoration (nommés girih, d'un mot persan signifiant « nœud »). Il croit aussitôt y reconnaître un pavage non périodique de Penrose, mais découvre quelque chose de plus : des étoiles à cinq et à dix branches aiguisent aussitôt sa curiosité. Comment ? Des pavages non-périodiques, cinq cents ans avant Penrose ?

Rentré à Harvard, il se met à scruter un maximum d'images d'art islamique médiéval et c'est là qu'il identifie cinq formes qui forment une trame à tous ces dessins. Il s'agit de cinq polygones très simples, dans lesquels il retrouve les angles des cerfs-volants et des fléchettes de Penrose : un décagone (angles intérieurs de 144°) et un pentagone réguliers (angles intérieurs de 108°), un losange avec des angles de 72° et 108°, un hexagone non régulier avec des angles de 72° et 144°, et une sorte de « nœud papillon » avec des angles de 216° et, à ses pointes, des angles de 72°. Les voilà, les tuiles de girih !

Ces « tuiles » pavent parfaitement le plan, à cause des valeurs de leurs angles, tous multiples de 36°, des longueurs de leurs côtés, toutes les mêmes, et de leurs symétries spécifiques. De plus, les contours (en bleu sur le dessin) qu'on peut y tracer, qui passent tous par les milieux des côtés, et coupent ceux-ci toujours sous le même angle, s'alignent parfaitement une fois les pavés assemblés pour former ces lignes si décoratives.

Peter Lu s'associe ensuite à Paul Steinhardt, son collègue de l'université de Princeton, spécialiste des quasi-cristaux, pour écrire un article relatant cette découverte (Science, 23 février 2007), qui est repris ensuite par la presse grand public (New York Times ou Iran Daily). Les deux chercheurs y décrivent bien sûr « leurs » tuiles et suggèrent aussi – prenant l'exemple du fronton du complexe funéraire de Darb-i Imam à Ispahan (Iran), datant de 1453 – qu'elles peuvent être découpées en « fléchettes » et « cerfs-volants » comme celles de Penrose. C'est bien ce que Lu avait vu dès le début !

Il existe aujourd'hui des jeux en bois reproduisant tuiles de girih et tuiles de Penrose, permettant de réaliser soi-même ses propres pavages islamiques…

Artisans géomètres ?

Plusieurs questions demeurent cependant : dans quelle mesure les artisans de ces œuvres remarquables de précision savaient-ils assez de mathématiques pour reproduire leurs dessins sans erreur sur de grandes surfaces ? L'usage de pavages comme ceux de Penrose était-il pure coïncidence ou relevait-il de l'application délibérée de connaissances géométriques avancées ?

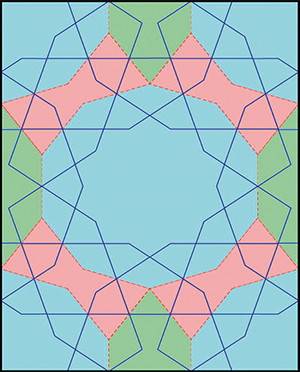
                     Couverture d'un Coran                         Le schéma correspondant.

                        du XIV^e siècle.

Peter Lu a obtenu la réponse à ces questions en consultant une autre de ses collègues, Gülru Necipoğlu, professeure d'art et architecture islamiques à Harvard et auteure d'un livre, Topkapi scroll: Geometry and Ornament in Islamic Architecture (« Le manuscrit de Topkapi : géométrie et décorations dans l'architecture islamique »). Le manuscrit en question, qui date du XV^e siècle, est le mieux conservé de ceux de sa catégorie. Long rouleau de presque trente mètres, sans texte, trouvé au palais Topkapi d'Istanbul, le centre administratif de l'Empire ottoman, il montre une suite de modèles de motifs qu'utilisaient vraisemblablement les artisans de l'époque pour réaliser leurs dessins. Complété par un système de grilles et de codes de couleurs mettant en évidence les symétries et les formes, ce manuscrit pouvait être vu comme le manuel de référence des dessinateurs de motifs muraux ou d'ornement de voûtes. D'ailleurs, le tombeau Darb-i Imam d'Ispahan peut effectivement faire référence aux documents du manuscrit, qui représente, tout comme ce monument, l'architecture de l'empire timouride (du nom de la dynastie qui a régné sur l'Asie centrale, la Perse et la Mésopotamie du milieu du XIV^e siècle jusqu'en 1506). Ce seraient donc les modèles du manuscrit de Topkapi qui auraient servi aux architectes et artisans de l'art islamique médiéval. Peter Lu dit y avoir reconnu les cinq tuiles de girih, et, mieux, en comparant ces dessins avec ceux d'un pavage de Penrose, il n'y a trouvé qu'un infime nombre d'erreurs, ce qui tendrait à prouver que la précision du dessin du fronton de Darb-i Imam n'était pas un simple hasard : les artistes avaient en main les éléments pour construire des pavages presque parfaits et, même si leurs connaissances mathématiques étaient incomplètes, dit Peter Lu, « il est raisonnable de penser qu'ils savaient ce qu'ils faisaient mathématiquement ».

Le manuscrit de Topkapi.