Comment décrire la symétrie d'une figure ? Il est nécessaire pour cela d'utiliser un langage mathématique. L'un des plus connus, réputé pour son efficacité, a été initié par Alexander Murray MacBeath (1923-2014), puis adapté par William Thurston (1946-2012) et John Horton Conway (né en 1937).

Attention, le mot « symétrie » utilisé dans cet article va au-delà de la symétrie par rapport à une droite ou un point. On parlera de symétrie quand une partie d'une figure peut être retrouvée avec la même échelle (on a affaire à une isométrie, une transformation bijective qui conserve les distances). D'ailleurs, le terme grec syn signifie « même » et métrie est la « mesure ». 

Une fois toutes les symétries d'une figure connues, il suffit de transformer le motif source en les lui appliquant afin de reconstituer la figure globale. On se limitera donc ici exclusivement aux isométries, directes ou indirectes, à savoir : les symétries centrales ou axiales (réflexions), les rotations, et leurs composées. 

Miroir, mon beau miroir…

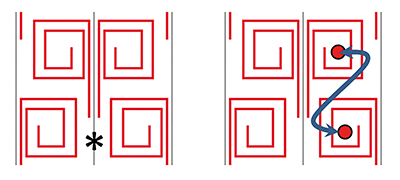
Une isométrie minimale d'une figure est une symétrie bilatérale, la symétrie classique par rapport à une droite, où la figure semble partagée par une ligne, le miroir (en gris sur les figures) : une partie de la figure est le reflet de l'autre partie dans le miroir. Un tel cas est symbolisé par sa signature, une étoile rouge dans la notation de Conway : * . Ainsi, une figure de signature * ne possède pas d'autres isométries qu'une symétrie de réflexion (identifiable dans le texte par la couleur rouge). Si une figure présente deux symétries miroirs, les deux droites se coupant en un point, sa signature sera désignée *2• . L'étoile représente le miroir, le chiffre 2 désigne deux miroirs, le point signale le fait que la figure possède un point fixe. Il peut évidemment y avoir plusieurs miroirs (matérialisés par des symboles * dans les schémas).

 Symétrie de réflexion dans un miroir (signature * ).

Deux symétries miroirs (signature *2• ).

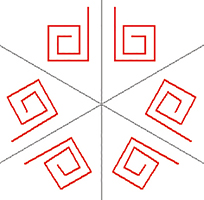
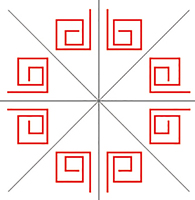
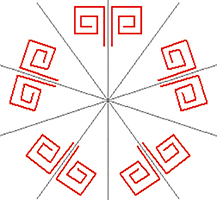
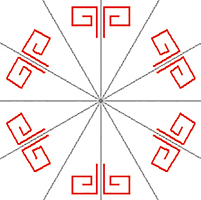
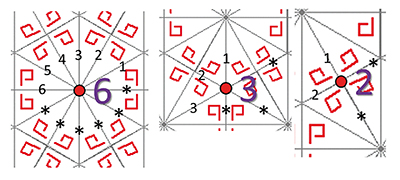
 De gauche à droite, figures de signatures respectives *3• , *4• , *5• et *6• .

Dans le sens qui est donné ici à la symétrie, une figure symétrique peut ne posséder aucun miroir. C'est le cas par exemple si elle présente une symétrie de rotation d'ordre 3, symbolisée par la signature 3• (comprendre : si l'on effectue une rotation d'angle 2π / 3 radians autour du point fixe • , alors la figure est inchangée). En termes de couleur, le bleu sera réservé aux symétries de rotation. Sur les schémas, le nombre m de petits tirets gris indique la présence d'une rotation d'angle 2π / m.

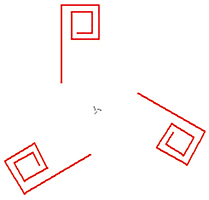
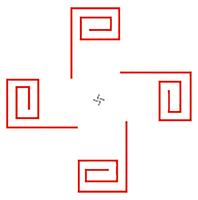
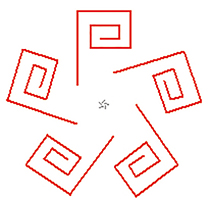
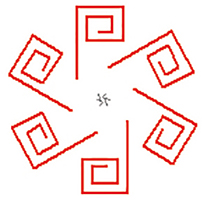
Figures de signatures respectives *3•, *4•, *5• et *6• .

Une figure finie ne peut avoir qu'une symétrie de type *, *2•, *3•, *4• (etc.) ou 1•, 2•, 3• (etc.). Ainsi, 1• correspond à une rotation de 2π, soit à l'identité (chaque point est transformé en lui-même). On sait donc décrire la symétrie de toute figure finie. Évidemment, de nombreuses figures n'admettent aucune symétrie d'aucune sorte.

Passons maintenant aux figures infinies, appelées les groupes cristallographiques (ou groupes de papiers peints, ou encore groupes de pavage du plan). Ce sont des figures pour lesquelles un même motif se répète dans les deux dimensions du plan, pour couvrir le plan tout entier. Les kaléidoscopes sont des figures générées par réflexions (par plusieurs miroirs). Le terme et l'objet ont été inventés en 1816 par le mathématicien écossais Sir David Brewster (1781-1868).

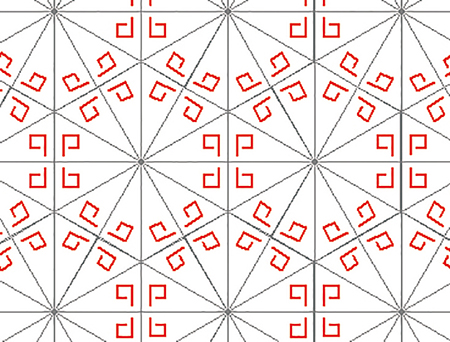
Motif kaléidoscopique de signature *632 .

Les symétries de signature *6•,*3• et *2•.

La région fondamentale  du motif *632.

Dans un kaléidoscope, certains points de la figure sont du type *6•, d'autres sont de type *3•, d'autres enfin sont de type *2•. Au final, ce motif sera symbolisé par la signature *632 (l'étoile se réfère au miroir, et il n'y a pas de point puisque, dans ce motif, il n'existe aucun point fixe). Les six symboles *632, *623, *362, *326, *263 et *236 sont équivalents. En pratique, on donne la liste dans l'ordre décroissant des nombres.

En se reflétant successivement dans les différents miroirs, un triangle suffit à paver tout le plan. Ainsi, la seule connaissance de ce triangle, la zone fondamentale, permet de reconstituer tout le pavage.

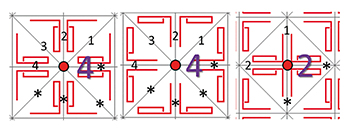
Les symétries de signature *4•,*4• et *2• .                      Figure de signature *442 

                                                                                            (le chiffre « 4 » est répété
                                                                                             car on a deux points
                                                                                              différents d'ordre 4).

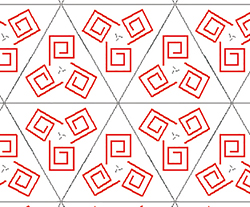
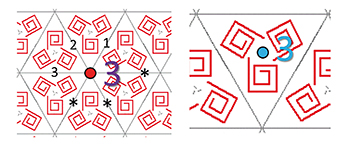
Motif de signature 3*3 .                                    Symétrie de signature *3• et 3• . 

                                                                                      La signature de ce motif est alors notée 3*3,
                                                                                     le premier « 3 » pour la rotation d'ordre 3
                                                                            puis *3 pour les trois miroirs.

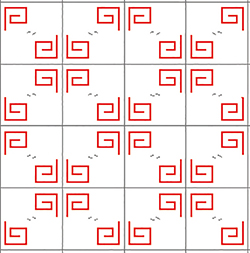
 Motif de signature 2*22 (deux types de symétrie, de signatures *2• et 2• ).

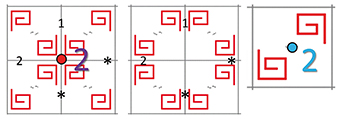
Les symétries de type *2•, *2• et 2•, donc de signature 2*22 .

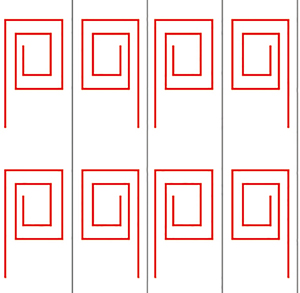
Sur la figure ci-dessous, il n'y a plus de miroir, mais trois types de rotation d'ordre 3. Mais il existe aussi des cas où les miroirs ne coupent pas (puisque la région délimitée par les miroirs est infinie !), comme pour la signature ** .

 Motif de signature 333 (sans miroirs).                                Symétries de signatures 3•, 3•, 3• .

       Motif de signature ** .                                             Les deux types de miroirs
                                                                                     (signature ** ).

Miracles et merveilles 

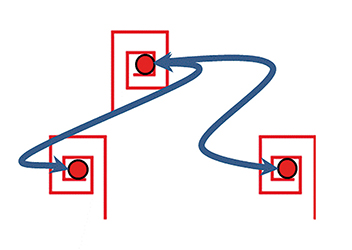
Dans la figure suivante, nous avons toujours des zones infinies délimitées par les miroirs, mais il se passe deux phénomènes : déjà, il n'y a qu'une sorte de miroirs. Ensuite, on peut passer d'une spirale à droite vers une spirale à gauche sans traverser un miroir ! La transformation s'appelle d'ailleurs un miracle dans la terminologie de Conway (on passe d'une figure dextrogyre à une figure sénestrogyre sans miroir). Depuis le début, ce sont les miroirs qui font passer de figures orientées dans un sens à des figures orientées dans l'autre sens ; on note x un miracle, et la signature de ce motif sera donc *x . Le miracle x est en fait une réflexion suivie d'une translation. Quand il y a plus de deux miracles, le motif prend la signature xx .

 Un motif de signature *x .                                Un miroir * et un miracle x .

Un motif de signature xx .                                         Deux miracles xx .

Enfin, on peut remplir l'espace d'un motif sans réflexion, ni rotation, ni miracle ; on a alors affaire à une merveille dans la terminologie de Conway. La signature d'une telle figure est o pour signaler l'absence des éléments déjà rencontrés. Le motif est en fait obtenu par deux translations. Une translation peut être vue comme la composition de deux réflexions, mais appeler cette nouvelle transformation « merveille » permet de contourner l'introduction des translations et met en avant le repérage des réflexions.

Un motif de signature o .

Maintenant que l'on sait caractériser la symétrie de tout groupe de pavage, il est possible d'énoncer le remarquable théorème des pavages : dans le plan, tous les groupes de pavage ne sont générés que par quatre types de symétries (réflexions, rotations, miracles et merveilles). Grâce à cette décomposition, il sera alors possible d'énumérer tous les groupes de pavage et de frises. Mais n'anticipons pas…

Le théorème des pavages 

À chaque symbole d'une signature, on peut attacher un poids. Ce poids se calcule explicitement par des considérations de topologie, ce qui sort du cadre de ce hors-série. On peut ensuite en déduire le poids total de la figure en sommant les poids des éléments des signatures. Le théorème des pavages permet de confirmer si ce poids total est correct, et donc si le calcul a été convenablement réalisé. Inversement, ce même résultat va nous aider à déterminer la signature d'une figure, et ensuite à énumérer les pavages des surfaces (plan, sphère, tore…).

La signature d'une figure est simplement une suite de symboles. À chaque symbole, on associe un poids, en suivant le tableau ci-dessus :

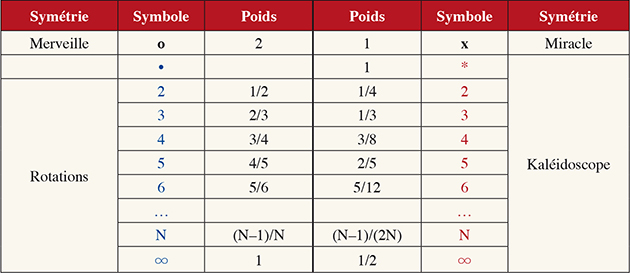
On constate que les poids des symboles de réflexions valent exactement la moitié des poids des symboles de rotations. Calculons le poids de certains motifs rencontrés précédemment :

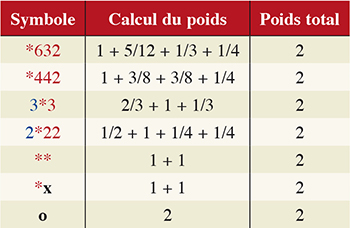
On remarque que le poids total d'un symbole d'un groupe de pavage du plan est toujours égal à 2. C'est en fait exactement ce qu'énonce le théorème des pavages ! Tout groupe de pavages du plan possède une signature de poids total égal à 2. La démonstration, qui sort du cadre de ce hors-série, s'appuie sur la formule d'Euler.

On peut maintenant produire une règle générale pour trouver la signature d'un pavage du plan :

1. Repérer les miroirs. S'il y en a plusieurs, limiter son attention à la plus petite portion du plan limitée par des miroirs (la région fondamentale), noter ses sommets, compter le nombre de miroirs se croisant à chaque sommet. Une région fondamentale ne peut pas être coupée par un miroir.

2. Rechercher les centres de rotations. Noter l'ordre de chaque centre de rotation. Un centre de rotation n'est jamais sur un miroir.

3. Y-a-t-il des miracles ? S'il n'en existe qu'un seul, noter x , s'il en existe plusieurs, noter xx .

4. S'il n'y a ni miroirs, ni rotations, ni miracles, chercher s'il existe des translations. Si oui, noter o .

La somme des poids doit faire 2. Si ce n'est pas le cas, vous avez dû faire une erreur ! L'application principale du théorème des pavages est l'énumération des groupes de pavage du plan. Voilà pour les groupes de pavage du plan. Mais que se passe-t-il sur d'autres surfaces ? Eh bien, il existe des extensions du théorème. Pour la sphère, par exemple, le poids total d'un pavage doit être égal à 2 – 2 / g, où g est l'ordre du groupe pavant la sphère (soit le nombre d'opérations qui vont transformer la figure de base en une autre). Ainsi, il existe quatorze façons de paver la sphère. Pour le pavage du plan, l'ordre du groupe est infini, ce qui correspond au cas où 2 / g tend vers 0. 

Un résultat qui défrise !

Un groupe de pavage du plan couvre le plan en s'étendant dans deux directions, une frise couvre le plan en s'étendant dans une seule direction. Pour les frises, il existe aussi un théorème des pavages : toute frise possède une signature comprenant un symbole infini dont le poids total fait 2. Que signifie ce symbole infini ? Imaginez que vous enrouliez une frise autour d'un cylindre. On peut alors déduire chaque élément de la frise par rotation autour du cylindre. Si le diamètre du cylindre tend vers l'infini, on tend vers notre frise plane. Et le nombre de rotations qu'il faut effectuer tend vers l'infini (ce que matérialise notre symbole). Ce troisième théorème des pavages permet d'énumérer les différents types de frises.