Un pavage du plan est un ensemble de parties, appelées pavés… mais qu'est-ce qu'un pavé ? Si l'on se limite aux pavés que l'on rencontre encore quelquefois dans les rues de nos villes, il s'agit approximativement de rectangles. Un ensemble de pavés pave un domaine du plan si leur réunion est égale à ce domaine et si l'intersection de deux quelconques d'entre eux est incluse dans leur frontière. L'idée se généralise au cas de polygones, convexes ou non, puis de domaines limités par des courbes plus sophistiquées.

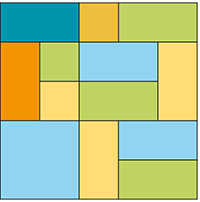
                Un exemple de pavage                                       Pavage du plan avec 

         d'un carré par des rectangles.                              des hexagones réguliers.

Des tomettes dans le plan

En mathématiques, on s'intéresse surtout aux pavages du plan entier. Les plus simples d'entre eux sont construits avec des pavés égaux, ou isométriques pour être plus précis. Il existe ainsi seulement cinq façons de paver le plan si l'on s'interdit de retourner les pavés. Il faut en ajouter douze autres si l'on se l'autorise. On peut en trouver un bon nombre en visitant l'Alhambra de Grenade. Certains prétendent les y avoir tous vus… ce qui est délicat, vu que de nombreuses pièces sont fermées au public. L'équipe de Tangente n'en a trouvé pour sa part qu'une grosse dizaine… Ces pavages sont périodiques, c'est-à-dire que l'on peut y trouver un motif de base qui se reproduit à l'infini au moyen d'un groupe d'isométries. Les plus simples d'entre eux sont utilisés dans nos maisons, comme ce dallage avec des tomettes.

Les artisans persans et arabes sont passés maîtres dans l'art de créer des pavages périodiques originaux, sans doute parce que, comme le judaïsme et le protestantisme dans sa version calviniste, l'islam proscrit la représentation des êtres humains ainsi que celle des animaux dans les lieux de culte. Les artisans décorateurs ont donc dû se tourner vers d'autres inspirations, les arabesques, les tuiles de Girih et les zelliges en particulier.

Mosaïques dans la mosquée du vendredi à Ispahan.

Ces pavages périodiques ont particulièrement intéressé les cristallographes car ils modélisent les arrangements des atomes dans les cristaux (voir Mathématiques et Chimie, Bibliothèque Tangente 43, 2012). Jusque dans les années 1960, on pensait que tout jeu fini de pavés pavant le plan pouvait le paver de manière périodique. Cela pouvait sembler simple bon sens, mais Roger Penrose montra que c'était faux en trouvant des structures apériodiques ! La question se retrouve également en cristallographie et, en ce qui concerne les pavages décoratifs, semble avoir été découverte longtemps avant, comme le montre une mosaïque découverte à Ispahan.

Au-delà du plan

La notion de pavage ne se limite pas au plan euclidien, les définitions se prêtent également aux plans non euclidiens. Cette idée se trouve chez les artistes Escher et Jos Leys, dont on présente ci-dessous un pavage du plan hyperbolique (vu, selon le modèle de Poincaré, comme un disque où la notion de distance dépend de l'éloignement du centre, comme si la marche des êtres vivant dans ce monde devenait plus difficile et plus lente quand ils s'approchent du bord du disque).

Un pavage du plan hyperbolique en hommage à Escher par Jos Leys. Pour les êtres imaginaires qui vivent à sa surface, tous les pavés sont identiques !