Attention, ce texte nécessite d'avoir lu l'article dans lequel signature et poids des pavages sont introduits. 

Dans un groupe de pavage du plan (ou groupe de papier peint), le même motif se répète à l'infini dans les deux dimensions afin de paver tout le plan. Derrière cette variété apparente se cache en fait un groupe qui va transformer un motif de base en tous les autres. Evgraf Fedorov a prouvé qu'il y a exactement dix-sept groupes. Cela se démontre facilement à condition de connaître le théorème du pavage du plan.

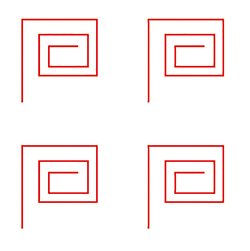
Le papier peint du symbole o .

Faisons les comptes… 

Ainsi, un groupe de papier peint doit avoir une signature de poids total 2. Le cas le plus simple est le symbole o (qui correspond à deux translations) : son poids vaut déjà 2.

En assemblant des symboles de rotations, on trouve quatre possibilités (voir la partie de gauche du tableau suivant). La combinatoire reste élémentaire.

Passons aux miroirs. Une signature de réflexion commence par * , dont le poids est 1. Il ne reste plus que 1 pour compléter. Déjà, la signature ** convient. Ensuite, puisque les poids des symboles de réflexions 2, 3, 4, 5, 6… N, 3 sont moitiés des symboles de rotations 2, 3, 4, 5, 6,…, N, 3 , nous avons les mêmes assemblages de symboles que pour ces dernières, soit *333, *442, *632 et *2222.

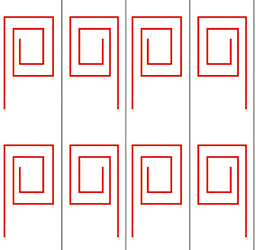
Le papier peint de signature ** .

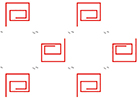
  Le papier peint            Le papier peint         Le papier peint            Le papier peint
de signature 333.       de signature 442.      de signature 632.       de signature 2222.

Le papier peint de signature *333.

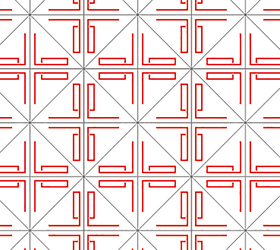
Le papier peint de signature *442.

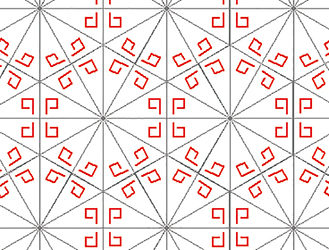
Le papier peint de signature *632.

Le papier peint de signature *2222.

Sans calcul !

Les papiers peints suivants sont obtenus en mélangeant les symboles. On remarque que si l'on remplace *NN par N* (où N est un entier) on ne change pas le poids de la signature. De même pour le remplacement du * final par un x dans une signature. Ainsi, *442 permet d'obtenir, sans calcul, 4*2. De même, *333 fournit directement 3*3. Ensuite, *2222 donne 2*22, puis 22*, et 22x . Enfin, ** produit *x et xx.

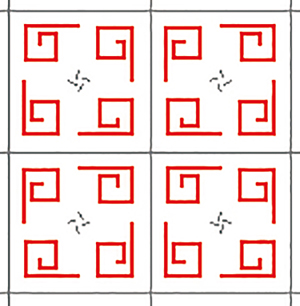
Le papier peint de signature 4*2.

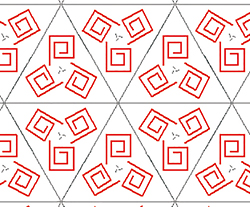
Le papier peint de signature 3*3.

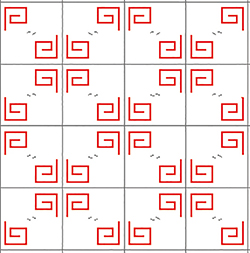
Le papier peint de signature 2*22.

Le papier peint de signature 22*.

Le papier peint de signature 22x.

Le papier peint de signature *x.

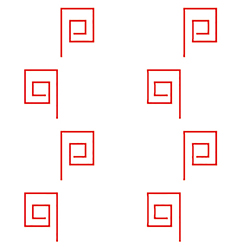
Le papier peint de signature xx.

Aucun autre assemblage de symboles ne possède un poids total de 2. Nous avons donc trouvé, sans difficulté une fois que les bonnes notations ont été introduites et que le théorème des pavages (qui est difficile) est disponible, les dix-sept groupes de pavage du plan.