Que d'éminents mathématiciens comme Lagrange, Euler et D'Alembert, et leur prince Gauss, se soient attaqué à sa démonstration confirme l'importance du théorème fondamental de l'algèbre, dénommé théorème de D'Alembert–Gauss. Il stipule que tout polynôme non constant à coefficients complexes admet au moins une racine. En conséquence, tout polynôme de degré n possède n racines complexes.

Le théorème de Gauss–Lucas 

La dérivée d'un polynôme de degré n étant un polynôme de degré n – 1, la question se pose naturellement d'une éventuelle relation entre les racines de ces deux polynômes. Un théorème existe pour les fonctions réelles. Quand vous redescendez à votre altitude de départ lors d'une randonnée en montagne, il est évident que vous avez dû cesser de monter à un moment pour redescendre. Vous avez alors atteint un maximum local de votre parcours, un endroit où la pente est nulle. C'est la signification du théorème de Rolle, qui spécifie que si une fonction réelle dérivable, comme un polynôme à coefficients réels, prend une même valeur en deux points, alors sa fonction dérivée s'annule, au moins une fois, entre ces deux points. Ainsi, si le polynôme du second degré P(x) = ax² + bx + c possède deux racines réelles, son polynôme dérivé P'(x) = 2a (x + b / 2a) s'annule en x = –b / 2a, demi-somme des racines de P. Cette remarque est d'ailleurs valable pour des racines complexes.

Une généralisation de cette propriété pour les polynômes complexes, utilisée depuis 1836 par Gauss et démontrée par Félix Lucas en 1874, énonce que les racines d'un polynôme dérivé P' appartiennent à l'enveloppe convexe de l'ensemble des racines du polynôme initial P.

Soit donc un polynôme complexe 

$P(z)=C\prod _{i=1}^r(z-a_i{)}^{{\mu }_i}$

dont les racines (a_i)_{1 ≤ i ≤ r}  ont pour multiplicité ( _{${\mu }_i$} )_{1 ≤ i ≤ r}. Si  _{${\mu }_i$} > 1, la racine a_i est multiple et est donc racine de P'(z). Ces racines de P', qui sont aussi racines de P, appartiennent donc, par définition, à l'enveloppe convexe des racines de P. Et une racine de P' au point B d'affixe b, si elle n'est pas racine de P, annule la dérivée logarithmique de P : 

$\frac{P^{\prime }(b)}{P(b)}=\sum _{i=1}^r\frac{{\mu }_i}{b-a_i}$  

En conjuguant cette expression, on obtient 

$\sum _{i=1}^r\frac{{\mu }_i}{\overline{b}-\overline{a_i}}=\sum _{i=1}^r\frac{{\mu }_i}{|b-a_i{|}^2}(b-a_i)=0$

 qui s'écrit sous forme vectorielle 

$\sum _{i=1}^r{\alpha }_i\overrightarrow{A_{i}B}=\overrightarrow{0}$

  avec 

${\alpha }_i=\frac{{\mu }_i}{|b-a_i{|}^2}>0$

Le point B, barycentre des racines (a_i)_{1 ≤ i ≤ r} de P avec des coefficients positifs, se situe donc bien à l'intérieur de l'enveloppe convexe de ces racines. C'est le théorème de Gauss–Lucas.

Pour un polynôme de degré 3, dont les racines ne sont pas alignées sur une droite, le théorème de Gauss–Lucas indique donc que les racines du polynôme dérivé sont intérieures au triangle des racines. Le théorème de Marden précise leur remarquable position, mais sa démonstration nécessite quelques propriétés affines…

Départ affine

Les transformations affines correspondent à des affinités, des « étirements », dans certaines directions, qui ne conservent pas les distances ni les angles, mais qui préservent les relations entre éléments, intersections, tangences et parallélismes. Par une transformation affine, les racines du polynôme image sont les images des racines du polynôme initial. Tout triangle (non dégénéré) peut ainsi avoir pour image un triangle équilatéral par une transformation affine.

Cette correspondance affine permet ainsi de démontrer le théorème des médianes dans tout triangle. En effet, la concourance des médianes, simple à démontrer dans un triangle équilatéral car les médianes sont aussi médiatrices, est conservée par une transformation affine. De même, le plus grand cercle inscrit dans un triangle équilatéral étant tangent à ses côtés en leur milieu, la plus grande ellipse inscrite dans un triangle est, pour ces mêmes raisons affines, tangente aux milieux des côtés.

C'est l'ellipse de Steiner, qui est l'ellipse de plus grande surface interne à un triangle. Elle coupe les médianes en leur tiers et son axe principal est la droite de régression orthogonale des sommets du triangle : la somme des carrés des distances des sommets à cette droite est minimale. Plus généralement, pour trois céviennes (droites passant par un sommet du triangle) concourantes, il existe une ellipse unique passant par les pieds de ces céviennes sur les côtés du triangle et tangente aux côtés en ces points.

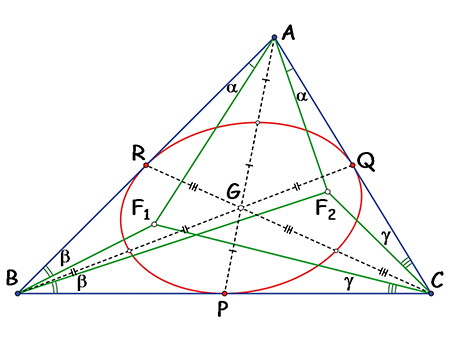
Théorème de Marden et ellipse de Steiner.

Passons maintenant à quelques propriétés elliptiques. D'un point M extérieur à une ellipse, traçons les tangentes à l'ellipse en G₁ et G₂, et les symétriques [MH₁] et [MH₂] des segments [MF₁] et [MF₂] par rapport à ces tangentes. La tangente en un point de l'ellipse étant la bissectrice extérieure des rayons vecteurs joignant ce point aux foyers, les angles $$ $\widehat{F_1{G}_1{I}_1}$ et $\widehat{F_2{G}_{1}M}$  sont égaux. Par construction,

$\widehat{F_1{G}_1{I}_1}=\widehat{H_1{G}_1{I}_1}$

et donc les points F₂, G₁ et H₁ sont alignés. Il en est de même pour les points F₁, G₂ et H₂. De plus, F₁G₁ = H₁G₁ et F₂G₂ = H₂G₂ par construction, d'où F₁H₂ = F₂H₁ = 2a, où a est le demi-grand axe de l'ellipse. Les triangles F₁H₂M et H₁F₂M sont donc isométriques et, par suite, les angles $\widehat{F_{1}M{G}_1}$ et $\widehat{F_{2}M{G}_2}$ aussi.

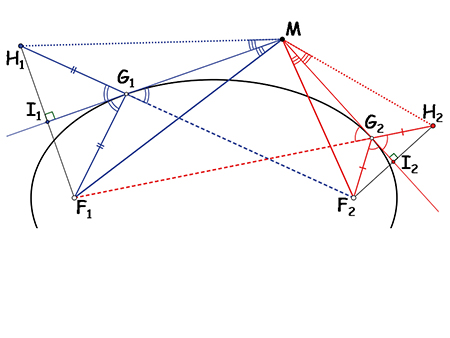
Quelques propriétés elliptiques.

À l'aide de ces propriétés, il devient possible de démontrer le théorème de Marden, qui stipule que, si les trois racines d'un polynôme définissent un triangle, alors son ellipse de Steiner a pour foyers les racines du polynôme dérivé. Puisque l'utilisation de polynômes particuliers n'enlève rien à la généralité par équivalence affine, on considère le polynôme P(z) = (z – 1)(z + 1)(z – u) = z³ – uz² + u, dont la racine u se situe dans le demi-plan supérieur {Im (u) > 0}. Alors les racines z₁ et z₂ du polynôme dérivé P'(z) = 3z² – 2uz – 1 sont telles que (z₁ + z₂) / 2 = u / 3 et z₁z₂ = –1 / 3. Puisque la moyenne des racines, (z₁ + z₂) / 2 = u / 3, est dans le demi-plan supérieur, au moins une des racines s'y trouve. D'autre part, puisque le produit des racines est réel négatif, arg(z₁) + arg(z₂) = π. Cette relation montre que les deux racines sont du même côté de l'axe des abscisses et que, puisque les angles ${\theta }_1$  = arg(z₁) et ${\theta }_2$  = arg(z₂) sont supplémentaires, les angles $\widehat{F_{1}OB}$ et $\widehat{AO{F}_2}$ sont égaux. L'ellipse de foyers F₁ et F₂ passant par l'origine est donc tangente au côté [AB] en son milieu O, comme l'ellipse de Steiner, tangente à chacun des côtés du triangle en son milieu.

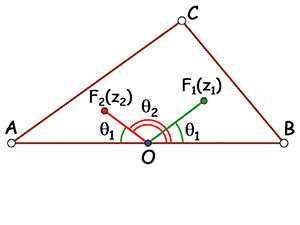
Les angles ${\theta }_1$ et ${\theta }_2$ sont supplémentaires.

On place maintenant l'origine O au sommet A du triangle, ce qui donne le polynôme

P(z) = z (z – 1)(z – u) = z³ – (1 + u)z² + uz,

toujours avec Im(u) > 0. Cette fois-ci, les racines z₁ et z₂ du polynôme dérivé P'(z) = 3z² – 2(1 + u)z + u sont telles que

(z₁ + z₂) / 2 = (1 +  u) / 3 et z₁z₂ = u / 3.

Sachant, d'après ce qui précède, que ces racines sont les foyers d'une ellipse tangente au côté [OB], elles appartiennent au demi-plan supérieur, et nous avons donc 0 <  ${\theta }_1$  <  ${\theta }_2$   < π. D'autre part, puisque z₁z₂ =  u / 3,   ${\theta }_1$  +   ${\theta }_2$   = arg(u). Par conséquent, l'angle entre (OF₂) et le côté [OC] est égal à  ${\theta }_1$  et l'ellipse de foyers F₁ et F₂ est aussi tangente au côté [OC].

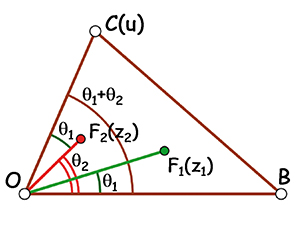
Quand l'origine O est un sommet du triangle.

En itérant le processus, on obtient une ellipse tangente aux trois côtés du triangle en leur milieu. Trois points et trois conditions de tangences déterminent six informations pour l'ellipse, qui n'a pourtant besoin que de cinq points pour être définie avec unicité. L'ellipse de Steiner, unique ellipse tangente aux trois côtés du triangle en leur milieu, a donc bien pour foyers les racines du polynôme dérivé du polynôme admettant les affixes des sommets du triangle pour racines. C'est le théorème attribué au mathématicien américain Morris Marden (1905–1991).

L'ellipse du parallélogramme

La démarche naturelle pour comprendre l'essence d'un théorème est de tenter une généralisation, que nous limiterons ici à un quadrilatère particulier, le parallélogramme.

Par de simples considérations de symétrie, il est manifeste que la plus grande ellipse contenue dans un carré est le cercle inscrit tangent aux quatre côtés en leur milieu. D'autre part, tout parallélogramme peut être transformé en un carré quelconque donné par une application affine bijective, c'est-à-dire de façon unique. Il suffit de composer une rotation, pour orienter deux côtés parallèlement à l'axe (Ox), une affinité d'axe (Oy) de la forme (x, y) $\mapsto$ (x,  $\alpha$ y), qui ajuste la hauteur du parallélogramme, avec une transformation qui « redresse » le parallélogramme, du type (x, y) $\mapsto$ (x +  $\beta$ y, y). La transformation inverse fait correspondre au cercle inscrit du carré une ellipse, tangente aux quatre côtés du parallélogramme en leur milieu. C'est l'ellipse de Steiner du parallélogramme.

L'analyse précédente peut être reproduite pour localiser les foyers de cette ellipse. Toujours à une transformation affine près, considérons un parallélogramme centré à l'origine, donc tel que ses sommets ont pour affixe u, v et leur opposé. Le polynôme associé à ce quadrilatère est alors P(z) = (z² – u²)(z² – v²), admettant pour polynôme dérivé P'(z) = 2z(2z² – (u² + v²)). Le centre du parallélogramme, d'affixe z = 0, est donc une racine de P', les deux autres racines lui étant symétriques.

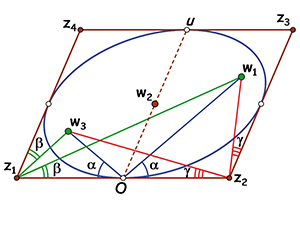
L'ellipse de Steiner d'un parallélogramme.

Pour reprendre la stratégie démonstrative du cas du triangle, considérons les sommets situés en z = –1, z = 1, z = u – 1 et z = u + 1, avec Im (u) > 0. Le parallélogramme est donc situé dans le demi-plan complexe supérieur, avec sa base inférieure sur l'axe des abscisses, et son centre à l'affixe w₂ = u / 2. On a alors

P(z) = (z² – 1)((z–u)² – 1).

Sachant que le centre du parallélogramme est racine du polynôme dérivé, ce dernier peut se mettre sous la forme P'(z) = 4(z – w₂)(z² – 2w₂z – 1). La moyenne des racines w₁ et w₃ est w₂, donc au moins une d'entre elles est dans le demi-plan supérieur. En fait, ce sont les deux, puisque de leur produit w₁w₃ = –1 on déduit que leurs arguments sont supplémentaires : arg(w₁) = a et arg(w₃) = π –  $\alpha$ . La tangente de foyers w₁ et w₃ qui passe par l'origine O est donc tangente à l'axe des x.

D'autre part, en utilisant les valeurs de la somme w₁ + w₃ = 2w₂ = u et du produit w₁w₃ = –1 des affixes des foyers, le calcul donne 

$\frac{(w_1-z_1)(w_3-z_1)}{(z_2-z_1)(z_4-z_1)}=\frac{(w_1-z_2)(w_3-z_2)}{(z_3-z_2)(z_1-z_2)}=\frac{1}{2}.$

Puisque deux nombres complexes dont le rapport est réel ont le même argument, on a

$arg\left[\frac{w_1-z_1}{z_2-z_1}\right]=arg\left[\frac{z_4-z_1}{w_3-z_1}\right]=\beta$

et

$arg\left[\frac{w_1-z_2}{z_3-z_2}\right]=arg\left[\frac{z_1-z_2}{w_3-z_2}\right]=\gamma$

D'après ce qui précède, l'ellipse déterminée par les foyers d'affixe w₁ et w₃ et qui passe par l'origine O est aussi tangente aux côtés passant par les points z₁ et z₂. Par symétrie, cette ellipse est tangente (en leur milieu) aux quatre côtés du parallélogramme. C'est l'ellipse d'aire maximale inscrite dans un parallélogramme.

Si le théorème de Marden peut se généraliser à un parallélogramme, ce n'est pas le cas pour un quadrilatère quelconque. Un quadrilatère postulant à une ellipse inscrite tangente à ses quatre côtés doit pouvoir être l'image par une transformation affine d'un quadrilatère circonscrit à un cercle, c'est-à-dire d'un quadrilatère dont la somme des côtés opposés est constante. C'est justement le cas d'un parallélogramme, image affine d'un carré.