Inventés dès le milieu du xvi^e siècle avant tout pour résoudre des équations, les nombres complexes n'ont acquis un statut mathématique qu'au xviii^e siècle, lorsque leurs propriétés algébriques ont été traduites géométriquement. Leur usage de « facilitateurs » de problèmes géométriques pouvait alors débuter…

Une histoire de nombres et de points

Représentation et multiplication des complexes selon Argand.

Lorsqu'en 1797 le Norvégien Caspar Wessel (1745–1818), arpenteur de son état, qui voyait sans doute dans les nombres complexes une manière de résoudre les triangles de son métier, présenta à l'Académie royale du Danemark son mémoire Essai de représentation analytique de la direction, il fut accepté car jugé d'un très bon niveau… mais resta dans l'oubli jusqu'à ce qu'un antiquaire le retrouve, en 1895 (!), où il fut enfin reconnu puis publié par Sophus Lie. L'approche de Wessel, qui utilise l'addition des « lignes possédant une longueur et une direction », nos actuels vecteurs, définit leur multiplication en ajoutant leurs angles polaires et en multipliant leur longueur.

En réalité, Wessel était un précurseur, car le Suisse Jean-Robert Argand (1768–1822), qui n'était pas non plus un mathématicien professionnel puisque comptable et libraire à Paris, publie en 1806, dans un petit livre cette fois, mais édité à compte d'auteur, Essai sur la manière de représenter les quantités imaginaires par des constructions géométriques. Le comble, c'est qu'il oublie de faire figurer son nom sur l'ouvrage, qui ne doit sa notoriété qu'à Jacques Français, frère du mathématicien alsacien François Français ! Voilà maintenant que paraît l'article dans les Annales de Gergonne, de manière anonyme. Argand, qui reconnaît son texte, en revendique la paternité et propose même quelques subtiles modifications. Rien de tel pour se faire connaître et déclencher une belle polémique sur le bien-fondé de la représentation géométrique des complexes face à leur simple utilisation algébrique.

C'est néanmoins le texte d'Argand qui reste dans les mémoires, avec ses définitions à partir de « moyennes proportionnelles » : \( \sqrt{-1}\) , représenté par KE, est moyenne de 1, représenté par KA, et –1, représenté par KI. Argand exprimera « ordinairement » sa « ligne dirigée » KA, qu'il écrira \( \overline{KA}\) par 1, puis  \( \overline{KI}\)  par –1,  \( \overline{KE}\) et  \( \overline{KN}\)  respectivement par  \( \sqrt{-1}\)  et  \( -\sqrt{-1}\) , à qui Euler a donné le nom de i et – i.

Additionner les « lignes dirigées » se fait, comme pour additionner les vecteurs, en construisant des parallélogrammes. Mais pour les multiplier ? Le principe d'Argand se fonde sur le fait que le rapport de deux rayons unitaires faisant entre eux les mêmes angles ne dépend que de cet angle. Ainsi, si  \( \widehat{AKB}=\widehat{CKD}\) , Argand écrira 

\( \overline{KA}:\overline{KB}::\overline{KC}:\overline{KD}\)

 ou 

\( \overline{KA}\times\overline{KD}=\overline{KB}\times \overline{KC}\)

 et comme  \( \overline{KA}=1, \)   \( \overline{KB}\times \overline{KC}=\overline{KD}\) Si les rayons ne sont pas unitaires, on les mettra sous la forme  \( m.\overline{KB}\)  ou  \( n.\overline{KC}\)  et le produit sera alors  \( mn.\overline{KD}.\)  Argand ira même jusqu'à noter r \( \theta\) la « ligne dirigée » de longueur r et d'angle \( \theta\) avec la direction principale, et à écrire 

\( r\theta=re^{\theta\sqrt{-1}}=r\sin\theta+r\cos\theta\sqrt{-1}\) .

Voilà donc réinventés géométriquement les nombres complexes, ce qui permettra d'éclairer d'un jour simplificateur certaines démonstrations de géométrie.

Les complexes en géométrie, pour quoi faire ?

Il est aisé de traduire en termes de nombres complexes les propriétés de nombreuses configurations géométriques. Tout d'abord, les notions élémentaires de géométrie, comme la distance de deux points, ont une expression complexe immédiate : si le point A a pour affixe a et B pour affixe b, la distance AB s'exprime par |a – b|, module de a – b. On peut aussi définir l'affixe du vecteur  \( \vec{AB}\)  par b – a, et exprimer la colinéarité ou l'orthogonalité de deux vecteurs. Soient  \( \vec{v}, \vec{v'}\)  d'affixes respectives z = a + ib et z' = a' + ib', alors 

\( \overline{zz'}=(aa'+bb')+i(a'b-ab')\)

 et ainsi, dire que  \( \vec{v}\)  est colinéaire à  \( \vec{v'}\) équivaut à dire que la partie imaginaire de  \( z\overline{z'}\)  est nulle, donc que \( z\overline{z'}\) est réel. C'est dire aussi qu'il est égal à son conjugué :  \( z\overline{z'}=\overline{z}z'\) . De même, dire que \( \vec{v}\) est orthogonal à \( \vec{v'}\) équivaut à dire que la partie réelle de \( z\overline{z'}\) est nulle, donc que \( z\overline{z'}\) est imaginaire pur, ou encore qu'il est égal à l'opposé de son conjugué :  \( z\overline{z'}=-\overline{z}z'\)  On peut tout aussi simplement exprimer l'angle des deux vecteurs \( \vec{v}\) et \( \vec{v'}\) , si  \( \vec{u}\)  est le premier vecteur de base :

\( (\vec{v},\vec{v'})=(\vec{u}, \vec{v'})-(\vec{u}, \vec{v})=arg(\vec{v'})- arg(\vec{v})= arg(\frac{\vec{v'}}{\vec{v}}).\)
 

On arrive maintenant à l'équation complexe d'une courbe (Γ), que l'on cherchera à mettre sous la forme f (z) = 0, où f est une application de \( \mathbb{C}\) dans \( \mathbb{C}\) , ce qui signifie que le point M d'affixe z appartient à (Γ) équivaut à f (z) = 0. Une façon simple d'écrire par exemple l'équation complexe d'une droite d passant par un point A d'affixe a et orthogonale à un vecteur d'affixe v est de dire que : M appartient à d si, et seulement si  \( \vec{AM}\) est orthogonal à  \( \vec{v}\) , soit 

\( (z-a)\bar{v}+(\bar{z}-\bar{a})v=0\)

soit encore 

\( z\overline{v}+\overline{z}v-(a\overline{v}+\overline{a}v)=0\)

Or,  \( a\bar{v}-\bar{a}v\)  est réel et la forme générale de l'équation complexe d'une droite est :  \( z\bar{v}+\bar{z}v-\lambda=0\)  avec \( \lambda\) réel.

Pour l'équation complexe d'un cercle (C) de centre A (d'affixe a) et de rayon R, on écrit que : M d'affixe z appartient à (C) équivaut à AM² = R², soit  \( (z-a)(\bar{z}-\bar{a})=R^2\) ou \( z\overline{z}-a\overline{z}-\overline{a}z+\left | a^2 \right |-R^2=0\) , et comme |a²| – R² est réel, l'équation complexe d'un cercle est :

  \( z\bar{z}-a\bar{z}-\bar{a}z+\mu=0\)

où \( \mu\) est réel.

On peut alors mettre à profit la forme de ces équations pour reconnaître certains lieux géométriques, comme l'ensemble des points M(z) dont le rapport des distances à deux points fixes A(a) et B(b) est une constante k. On trouve, si k = 1, une équation du type 

\( (\overline{a-b})z+(a-b)\bar{z}-(|a^2|+|b^2|)=0\)

 qui est bien l'équation d'une droite : c'est la médiatrice de [AB]. Si k est différent de 1, on tombe sur l'équation 

\( z\bar{z}-\left(\frac{a-k^2b}{1-k^2}\right)\bar{z}-\left(\frac{\overline{a-k^2b}}{1-k^2}\right)z+|a^2|-k^2|b^2|=0\)

 qui est bien celle d'un cercle, le cercle d'Apollonius des points A et B pour le rapport k : centré sur la droite (AB), il a pour diamètre [PQ], où P et Q sont les barycentres de {(A, 1), (B, k)} et de {(A, 1), (B, – k)}. Tout ceci est établi grâce aux équations complexes.

Allons plus loin et exprimons par exemple qu'un triangle ABC, où les abscisses respectives de A, B et C sont a, b et c, est équilatéral direct. Il suffit d'écrire que  \( \vec{BA}\) est l'image de \( \vec{BC}\) dans la rotation de centre A et d'angle π / 3, soit 

\( z_{\vec{BA}}=e^{i\pi/3}z_{\vec{BC}}\)

ou encore a – b = e^iπ/3 (c – b). Une facilité est ici de mise : elle consiste à écrire j = e^2iπ/3 et à remarquer que e^iπ/3 = – j². La relation précédente devient alors a + bj + cj² = 0, condition qu'il suffira de vérifier pour voir si ABC est équilatéral direct. On aura, pour un triangle équilatéral indirect, a + bj² + cj = 0.

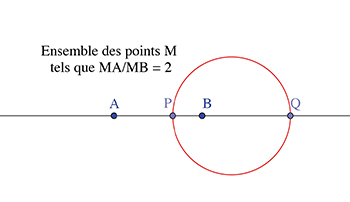
Le cercle d'Apollonius de A et B, pour le rapport k = 2.

De même, exprimer qu'un quadrilatère ABCD, où les affixes respectives des sommets sont a, b, c et d, est un parallélogramme devient très simple, en écrivant par exemple que ses diagonales ont même milieu, soit a + c = b + d.

Si l'on ajoute la condition supplémentaire que ce quadrilatère soit un carré direct, il faudra en outre que l'image par la rotation vectorielle d'angle + π / 2 du vecteur  \( \vec{BD}\) soit le vecteur \( \vec{AC}\) , soit, en termes de nombres complexes, (c – a) = i(b – d), ou encore a + ib = c + id.

Même la condition de cocyclicité de quatre points ABCD s'exprime très rapidement en traduisant que les angles  \( (\vec{DB},\vec{DA})\) et  \( (\vec{CB},\vec{CA})\) sont égaux modulo π :

\( arg(\frac{a-d}{b-d})=arg(\frac{a-c}{b-c})\)

soit

\( arg(\frac{a-c}{b-c}:\frac{a-d}{b-d})=0\)  

C'est dire que \( \frac{a-c}{b-c}:\frac{a-d}{b-d}\) est réel. On retrouve là la notion de birapport, si fructueuse en géométrie projective. Vous voyez comme tout devient simple, avec les complexes !

De beaux problèmes ainsi résolus

Les « ha ha », sortes d'éclairs de génie mathématiques, permettaient de se sortir de situations difficiles (voir Tangente 172). Un exemple en est un résultat dont Monge a donné une démonstration originale. L'énoncé tient en quelques mots : trois cercles de rayons inégaux ont des tangentes communes extérieures qui se coupent en trois points ; montrer que ces points sont alignés. Monge, pour le prouver, avait fait un détour par l'espace, en considérant des cônes tangents à des sphères. Il aurait pu tout aussi bien faire un détour par les complexes…

En effet, avec les notations de la figure, en prenant, de manière astucieuse, le point A comme origine, on peut considérer l'homothétie positive de centre A qui transforme le cercle rouge en cercle bleu. Son rapport est le rapport m du rayon « bleu » sur le rayon « rouge » et son expression en termes de nombres complexes est z' = mz. De même, en appelant b et c les affixes respectives des points B et C, l'homothétie positive de centre B qui transforme le cercle bleu en le cercle jaune a pour expression complexe z'' – b = n (z' – b), d'où z'' = nmz + (1 – n)b, ce qui permet de déduire deux choses : déjà que la transformation qui permet de passer directement du cercle rouge au cercle jaune est une homothétie (car elle en a la forme complexe), ensuite que le point fixe C de cette transformation a pour affixe  \( c=\frac{(1-n)b}{1-mn}\)  et qu'il est aligné avec l'origine A et le point B.

Un autre problème, plus spectaculaire encore, est celui des cercles de Clifford, dont on doit la démonstration au mathématicien et philosophe britannique William Kingdom Clifford (1845–1879). L'énoncé, d'apparence touffue, se fait mieux comprendre à la lecture du dessin :

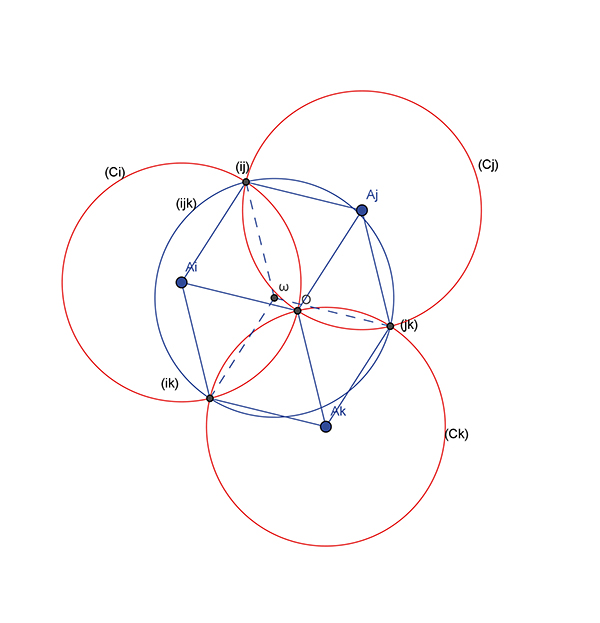
Trois cercles de Clifford.

(C_n) est une famille infinie de cercles de même rayon r, deux à deux distincts et qui passent tous par un même point O. On note commodément (ij) le point d'intersection autre que O des cercles C_i et C_j puis (ijk) le cercle circonscrit au triangle de sommets les points (ij), (ik) et (jk), pour des indices i, j et k deux à deux distincts.

On peut alors (merci les complexes !) commencer par prouver que le cercle que (ijk) a pour rayon r. Pour cela, deux remarques préliminaires s'imposent :

Le cercle (C_i), dont le centre A_i pour affixe a_i, est l'ensemble des complexes z de la forme z = ai +  \( \lambda\) , où \( \lambda\) est un complexe de module 1, puisque |z – a_i| = 1 ;

Écrire que ce cercle (C_i) passe par le point O se traduit par |a_i| = r.

Compte tenu de ces propriétés, le résultat se démontre en prouvant d'abord que le point (ij) a pour affixe z_ij = a_i + a_j, car le quadrilatère OA_j(ij)A_i est un losange. Or, il en est de même pour les quadrilatères OA_j(jk)A_k et OA_i(ik)A_k, ce qui permet d'envisager le polygone dont le contour est (ij)A_i(ik)A_k(jk)A_j comme une vue en perspective d'un cube d'arête r dont l'origine O et le point v_ijk d'affixe a_i + a_j + a_k, seraient deux sommets opposés. Et c'est ce point v_ijk qui est le centre du cercle (ijk), puisque |v_ijk – z_ij| = |a_k| = r; de même, |v_ijk – z_jk| = |a_i| = _r, et |v_ijk – z_ik| = |a_j|= r.

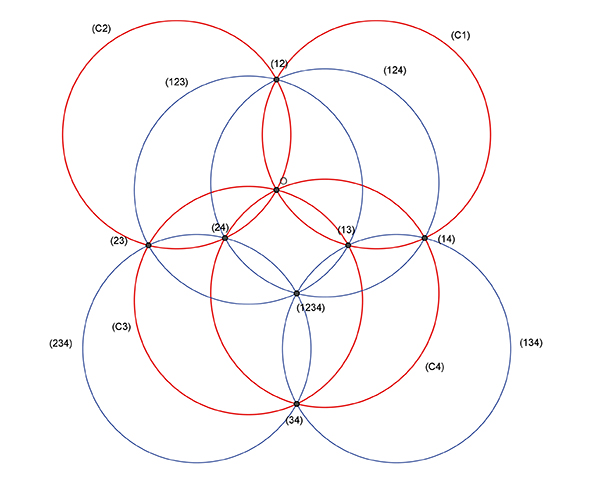Quatre cercles de Clifford.

Le résultat s'étend : en considérant quatre indices distincts, par exemple 1, 2, 3, 4, les cercles (1 2 3), (1 2 4), (1 3 4) et (2 3 4) passent tous par un même point, que l'on notera (1 2 3 4). On obtient avec les cinq points (1 2 3 4), (1 2 3 5), (1 2 4 5), (1 3 4 5) et (2 3 4 5) un résultat du même style : ils appartiennent tous à un même cercle, de rayon r, puis les \( \binom{6}{5}\)   cercles (12345), (12346), (12356), (12456), (13456), (23456) passent par un même point, etc. jusqu'à l'infini !

L'invention de Jean-Robert Argand qu'en 1813 le mathématicien franc-comtois François-Joseph Servois qualifiait encore de « masque géométrique » a pourtant mis longtemps à s'établir, et il a fallu attendre jusqu'à la publication de la Théorie des résidus biquadratiques de Gauss en 1883 pour qu'elle prenne toute sa place et nous permette aujourd'hui encore d'arriver à de bien belles démonstrations.