Cette transformation géométrique associe à chaque point M différent de l'origine le point M' aligné avec O et M tel que OM × OM' = 1. Son principal intérêt est de laisser stable l'ensemble des cercles et droites du plan. Son expression complexe est tout simplement  \( 1/\bar{z}\)

L'inversion peut être utilisée pour démontrer le théorème de Mohr–Mascheroni, qui affirme que toute construction à la règle et au compas peut être effectuée au compas seul. D'un point de vue plus pratique, c'est sur l'inversion que repose l'inverseur de Peaucellier, un dispositif qui doit son nom à son inventeur et qui transforme un mouvement circulaire en mouvement rectiligne.

Image d'une droite par l'inversion

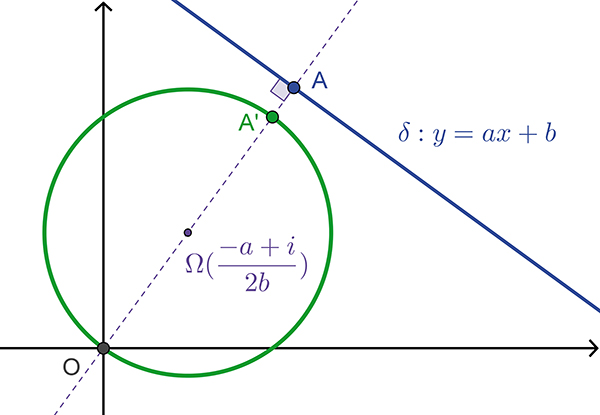
Considérons une droite Δ d'équation y = ax. Tout point de cette droite à une affixe z de la forme z = x + iax. On en déduit que 

\( \frac{1}{\overline{z}}=\frac{1+ia}{x(1+a^2)}\)

On remarque que 

\( Im\left ( \frac{1}{\overline{z}}\right )=aRe\left (\frac{1}{\overline{z}}\right )\)

 En fait, l'image de Δ (privée de l'origine) par l'inversion est la droite Δ elle-même ! D'autres cas peuvent se traiter aisément. Considérons une droite D d'équation x = k (avec k non nul). Tous les points de D ont une affixe z de la forme z = k + iy. Si l'on note  \( \frac{1}{\bar{z}}=x'+iy'\)  on trouve

\( x'=\frac{k}{k^2+y^2}\)

et

  \( y'=\frac{y}{k^2+y^2}\) .

On peut alors s'assurer que 

\( \left(x'-\frac{1}{2k}\right)^2+y'^{2}= \left(\frac{1}{2k}\right)^2\)

Cela permet d'établir que l'image de D est le cercle (privé de l'origine) de rayon 1 / (2 | k |) dont le centre a pour affixe 1 / 2k. 

Après quelques calculs, on peut aussi établir que l'image d'une droite \( \delta\)  d'équation y = ax + b (avec b non nul) par l'inversion est le cercle C (privé de l'origine) de centre Ω (d'affixe \( \frac{-a+i}{2b}\) ) et de rayon  \( R=\frac{\sqrt{a^2+1}}{2|b|}\) . Géométriquement, \( \delta\)  et (OΩ) sont perpendiculaires et se coupent en un point A ; C est le cercle de diamètre [OA'], où A' est l'image de A par l'inversion.

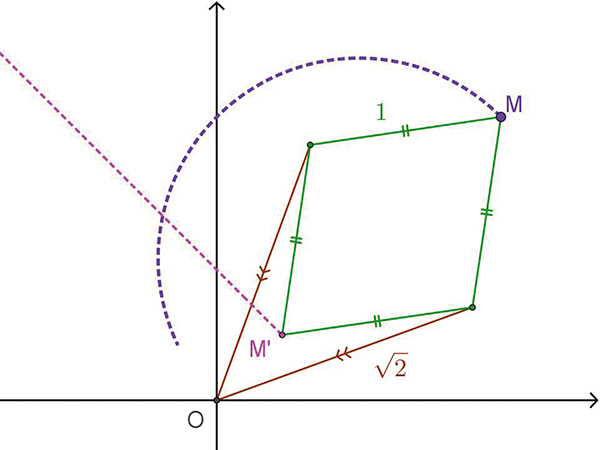
L'inverseur de Peaucellier

Le dispositif mécanique inventé par Charles Peaucellier est composé de six segments articulés. Sur le schéma suivant, les quatre segments verts forment un losange et les deux segments marron sont de même longueur. Lorsque le point M décrit un cercle bien choisi (passant par O), M' décrit une droite (et réciproquement). En effet, M' est alignés avec O et M et, si les longueurs des segments sont bien choisies (dans un rapport de  \( \sqrt{2}/2\) ), alors OM × OM' = 1. Autrement dit, M' est l'image de M par l'inversion !