La plus simple des rotations consiste sûrement à effectuer un demi-tour. Plaçons-nous dans le plan complexe d'origine O et considérons un point M d'affixe z = x + iy. Son image M' par la rotation de centre O et d'angle π radians (ou 180 °) a pour affixe z' = –x – iy. On a donc z' = –1 × z.

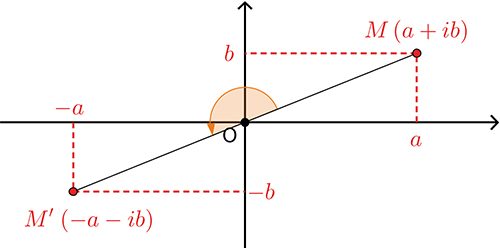
Et pour effectuer un quart de tour seulement ? Existe-t-il un nombre a tel que cette rotation soit décrite par une relation du type z' = az ? Si c'est le cas, on aurait a² = – 1. En effet, appliquer deux fois une rotation d'un quart de tour revient à effectuer un demi-tour ! Les seules solutions sont a = i et a = – i : tout dépend du sens dans lequel on tourne.

Une autre façon de voir les rotations

En fait, ce petit résultat se généralise assez facilement. Les rotations de centre O et d'angle \( \theta\) correspondent exactement aux applications qui, à z, font correspondre \( z' = e^{i\theta} z.\)

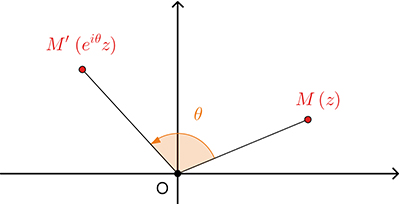
Et si le centre de la rotation n'est pas l'origine du repère ? La situation n'est pas beaucoup plus difficile, il suffit de faire appel aux translations. Comment ces dernières sont-elles décrites dans le cadre des nombres complexes ? Par une addition, tout simplement ! Appliquer à un point la translation de vecteur \( \vec{u}\binom{a}{b}\)   revient à ajouter à son affixe le nombre complexe a + ib.

Revenons à notre rotation d'angle \( \theta\) et de centre \( \Omega\) d'affixe \( \omega\) . Comment l'obtenir en combinant des translations et des rotations de centre O ? L'idée est la suivante : on applique d'abord une translation de vecteur  \( \vec{\Omega O}\)   pour se ramener à l'origine, on effectue ensuite une rotation de centre O et d'angle \( \theta\) , puis on enchaîne finalement avec une translation de vecteur  \( \vec{O \Omega}.\)   Dans le cadre des nombres complexes, nous avons fait correspondre à z le nombre

\( z'=e^{i\theta}(z-\omega)+\omega\)

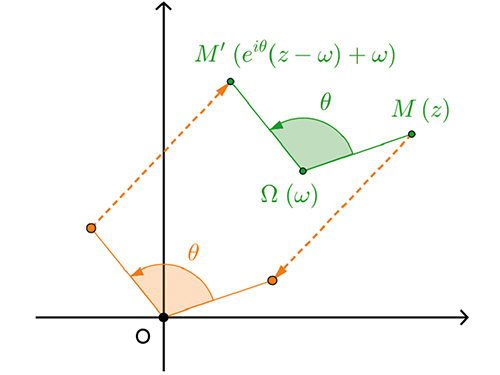
La transformation complexe obtenue est de la forme \( z\mapsto e^{i\theta}z+b\) (avec \( b=\omega(1-e^{i\theta})\) ). En fait, cette correspondance est « parfaite » dans le sens où toute transformation du type \( z\mapsto e^{i\theta}z+b\) correspond bel et bien à une rotation d'angle \( \theta\) (ou à une translation si jamais \( \theta\) , exprimé en radians, est un multiple de 2π). On retrouve d'ailleurs facilement l'affixe du centre en résolvant l'équation \( z = e^{i\theta}z+b\) .

Des résultats qui se conjuguent bien

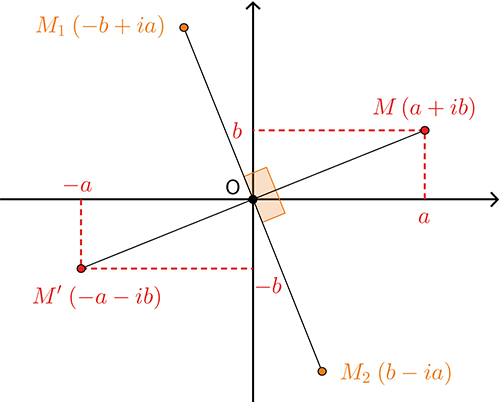
Les rotations et les translations conservent les distances ; on dit que ce sont des isométries. Mais ce ne sont pas les seules : il y aussi les symétries axiales ! L'une d'elles en particulier se décrit facilement à l'aide des nombres complexes ; voyez-vous laquelle ? C'est celle par rapport à l'axe des réels (ou l'axe des abscisses) : il suffit de conjuguer ! L'image du point M d'affixe z par cette symétrie est le point M' d'affixe  \( \bar{z}\) .

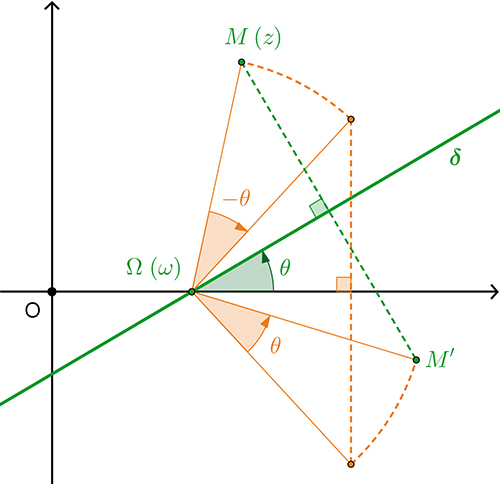
Comme précédemment, la symétrie par rapport à n'importe quel axe \( \delta\) peut être décrite par une transformation complexe en se ramenant à un cas bien connu. Par exemple, dans le cas où  \( \delta\)  coupe l'axe des abscisses en Ω avec un angle \( \) \( \theta\) , la symétrie d'axe  \( \delta\)  s'obtient comme composition (« enchaînement ») de la rotation de centre Ω et d'angle –  \( \theta\) , de la symétrie par rapport à l'axe des réels, et enfin de la rotation de centre Ω et d'angle \( \theta\) . On sait décrire ces trois transformations sous forme complexe, et un calcul (un peu long) permet de constater que la symétrie d'axe  \( \delta\) correspond à une transformation complexe de la forme  \( z\mapsto a\bar{z}+b\) où a  \( a\)  est de module 1.

Là aussi, avec un peu d'attention, on peut remarquer que la correspondance entre transformations géométriques et transformations complexes est idéale. Toute application de la forme  où a est de module 1 correspond en fait bien à une symétrie axiale ou à une symétrie axiale suivie d'une translation (ce qu'on appelle aussi symétrie glissée).

Comment savoir si l'on a affaire à une symétrie ou à une symétrie glissée ? Rien de plus simple : on applique deux fois la transformation ! Pour une symétrie, cela ne change rien (on revient au point dont on est parti). Assurez-vous par exemple que 

\( \phi_1 \, : \, z \mapsto i\bar{z}+(1-i)\)

est une symétrie, alors que 

\( \phi_2 \, : \, z \mapsto i\bar{z}+(2-i)\)

est une symétrie glissée.

Ainsi, les isométries du plan correspondent exactement aux applications complexes de la forme \( z \mapsto az + b\) ou \( z \mapsto a\bar{z} + b\) où a est un nombre complexe de module 1. Rien de bien méchant finalement !

Tournons, tournons !

Attardons-nous un moment sur l'étude des rotations. Quelle transformation obtient-on en enchaînant deux rotations ? Ici, le point de vue complexe… simplifie bien les choses ! Considérons donc deux rotations, r et r' de centres respectifs Ω et Ω' (d'affixes respectives  \( \omega\) et \( \omega\) ') et d'angles \( \theta\) et \( \theta\) '. On a donc, du point de vue des applications complexes,

\( r (z) = e^{i\theta} (z - \omega) + \omega \; \textrm{ et } \; r''(z) = e^{i\theta} (z - \omega') + \omega'.\)

L'enchaînement de ces deux rotations, r puis r', est donc une isométrie \( \phi\) définie par  :

\( \phi(z) = e^{i\theta'} (e^{i\theta}(z - \omega) + \omega - \omega')+\omega'.\)

En développant, on a :

\( \phi(z) = e^{i (\theta+\theta')} (z - \omega) + e^{i\theta'}( \omega - \omega')+\omega'\)

Plusieurs cas se présentent. Supposons que \( \theta+\theta'=2k\pi\) , avec k un entier relatif. L'expression de \( \phi\) se simplifie et on a alors

\( \phi(z)=z+e^{i\theta'}(\omega-\omega')+\omega'-\omega.\)

La transformation obtenue est donc dans ce cas une translation ! Comme \( e^{i\theta'}(\omega-\omega')+\omega'\) est l'affixe de l'image de Ω par r', on en déduit même que c'est la translation de vecteur   \( \overrightarrow{\Omega r' (\Omega)}.\)

Étudions maintenant le cas où  \( \theta+\theta'\) n'est pas un multiple de 2π. Si Ω et Ω' sont confondus, alors

\( \phi(z)=e^{i(\theta+\theta')}(z-\omega)+\omega\)

La composée des deux rotations de même centre est encore une rotation de même centre, il suffit juste d'additionner les angles. Aucune surprise !

Si Ω et Ω' ne sont pas confondus, alors \( \phi(z)\) est de la forme \( e^{i(\theta+\theta')}z+b\) avec

\( b=-e^{i(\theta+\theta')}\omega+e^{i\theta'}(\omega-\omega')+\omega'\)

C'est donc encore une rotation, d'angle \( \theta+\theta'\) , dont le centre a pour affixe l'unique solution de l'équation \( z=e^{i(\theta+\theta')}z+b\) , c'est-à-dire 

\( \frac{b}{1-e^{i(\theta+\theta')}}.\)

La boucle est bouclée !