Si vous demandez à votre voisin de choisir « un nombre au hasard », il y a de grandes chances pour que la réponse soit un entier naturel. Très peu de personnes vous répondront –2, 1/3,
Les entiers naturels sont en effet les premiers nombres que l'on rencontre : ils nous servent à dénombrer, ce que l'on fait depuis tout petit. Les nombres complexes ne sont étudiés que plus tard : il est préférable d'avoir déjà vu ce qu'est une équation du second degré pour pouvoir en comprendre l'utilité. Ce qui fait la particularité des nombres complexes, c'est bien sûr leur partie imaginaire, qui a donné du fil à retordre aux mathématiciens durant des siècles pour enfin leur accorder un statut valide au sein des mathématiques. Ils étaient d'ailleurs autrefois appelés nombres impossibles car ils avaient été créés pour résoudre des équations qui n'avaient pas de solution.
L'un des premiers à comprendre leur importance est René Descartes, qui, le premier, introduit les termes « nombres imaginaires » lorsqu'il étudie le nombre de racines des polynômes de degré au moins égal à 2. Il désigne alors des racines « vraies » (positives) et des racines « fausses » (négatives), qui peuvent être réelles ou « seulement imaginaires ». Il ne donne pas encore une validité à ces nouveaux nombres mais emploie déjà un vocabulaire moins radical. Ainsi, en mathématiques, l'impossible peut être contourné dès lors que l'on fait appel à son imagination : l'imagination, bien plus qu'un esprit rationnel, est indispensable à la pratique des mathématiques !
Les ensembles de Julia et la nouvelle calculatrice Graph 90+E
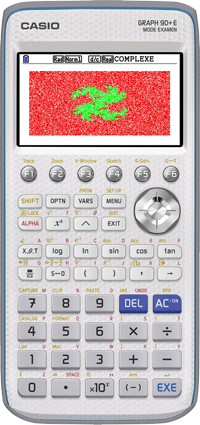
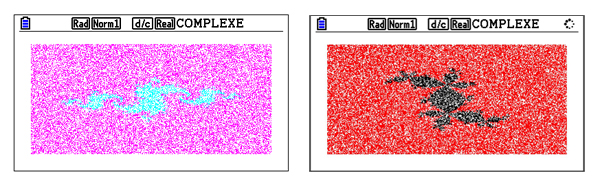
Dans les siècles qui ont suivi, les mathématiciens ont essayé de donner une légitimité aux nombres complexes, en particulier en cherchant à leur donner une représentation géométrique, puisque pouvoir visualiser un objet lui donne « plus de réalité ». Ils ont alors compris que l'on pouvait assimiler un nombre complexe z à un point P du plan, en associant les coordonnées de P aux parties réelles et imaginaires de z. Les abscisses sont leurs parties réelles et les ordonnées leurs parties imaginaires. Et cela donne parfois des représentations particulièrement intrigantes, comme les ensembles de Julia (du nom du mathématicien Gaston Julia), qui sont des ensembles particuliers de nombres complexes. Qui aurait pu penser que l'on obtienne de tels dessins en construisant ces ensembles ?
Soient z et c deux nombres complexes. On considère la suite ((zn)n ≥ 0 ) définie par zn+1 = z2n + c et z0 = z. On appelle ensemble de Julia rempli associé à c (et l'on note Jc) l'ensemble des nombres z tels que, pour tout entier n, le module de zn reste borné. Si le module d'un terme zn ou de c est supérieur à 2, alors la suite diverge (le module de zn tend vers l'infini avec n). D'autre part, comme une calculatrice ne peut calculer le module de zn pour toutes les valeurs de n, il est nécessaire de définir un nombre maximum I d'itérations. Plus ce nombre sera grand, plus le dessin sera précis… mais plus le calcul sera long.
Ci-dessous est figurée une approximation d'un ensemble de Julia en utilisant la nouvelle calculatrice graphique CASIO Graph 90+E. Avec son grand écran couleur et son menu Graphes 3D permettant d'étudier la géométrie dans l'espace, cette calculatrice permet de mieux visualiser les différentes représentations mathématiques. Vous allez pouvoir le constater par vous-même avec les résultats de notre algorithme pour différents nombres.