Traité comme un épiphénomène par Euclide, Archimède ou Apollonius, le problème des tangentes est devenu beaucoup plus prégnant au XVIIe siècle où l'idée « d'approcher le courbe par le droit » a guidé les travaux de Fermat, Torricelli ou Roberval et des géomètres en général. Cette quête les a menés à la notion actuelle de tangente, donc de dérivée, et d'asymptote, donc de limite à l'infini, bâtissant tous les concepts de l'analyse.
Tangentes : une aventure mathématique
Tangente, l'aventure mathématique. Si notre revue a pris ce nom, c'est qu'il évoque l'une de ces équipées dont les mathématiques ont le secret, celle de parcourir l'histoire, d'apparaître, de disparaître puis de réapparaître sous une autre forme, grâce à une nouvelle approche, pour arriver à une notion plus actuelle, plus générale, en un mot plus aboutie.
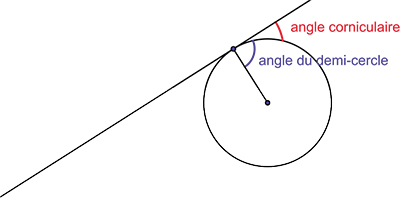
La notion de tangente n'était pas la préoccupation majeure des géomètres de l'Antiquité, mais certains l'ont évoquée à leur manière. Euclide (IIIe siècle avant notre ère) dans ses Éléments évoque la tangente au cercle, sans parler d'autres courbes, proposant au Livre III sa définition : « Une droite qui, rencontrant un cercle et prolongée, ne le coupe pas, est dite tangente au cercle. » Il nous offre même une propriété caractéristique de cette fameuse droite : « La droite menée à angles droits avec le diamètre du cercle à partir d'une extrémité du cercle tombera à l'extérieur du cercle, et dans le lieu compris entre la droite et la circonférence, une autre droite ne sera pas intercalée ; en outre, d'une part l'angle du demi-cercle est plus grand, d'autre part l'angle restant plus petit que tout angle rectiligne aigu. » L'angle « restant », le fameux angle corniculaire, l'angle entre la courbe et sa tangente, a fait couler beaucoup d'encre chez les géomètres, qui se demandaient entre autres s'il pouvait être bissecté.
Archimède, à peu près à la même époque, dans son traité Des spirales, démontre que « si une droite est tangente à une spirale, elle sera tangente en un seul point ». Rappelons qu'une spirale d'Archimède est l'ensemble décrit par un point M parcourant à vitesse constante une demi-droite [Ox) du plan, cette dernière tournant elle-même autour de O à vitesse angulaire constante. Il propose de la tangente à cette courbe une construction approchée, d'ailleurs dans le but de régler le problème de la quadrature du cercle. Apollonius, lui, dans le même temps, cherche à étendre aux coniques les propriétés du cercle et de ses tangentes.
On a pratiqué essentiellement dans l'Antiquité une géométrie de longueurs mais c'est par des démarches très diverses que la notion de tangente va être approchée à partir du xviie siècle. Il faut à présent pouvoir répondre à la demande : on a créé de nouvelles courbes et il faut inventer les tangentes qui vont avec.
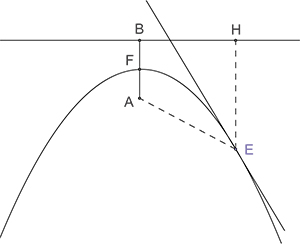
Sur la construction de la tangente à la parabole de foyer A et de directrice la droite (BH) que décrit le point E, tel que EH = EA, reprenons le texte et les notations de Roberval : « Le mouvement du point E décrivant la parabole est composé de deux mouvements droits égaux, dont l'un est [selon] la ligne AE et l'autre est la ligne HE sur laquelle il se meut de même vitesse. »
Avec Pierre de Fermat (vers 1601-1665) et René Descartes (1596-1650), on pratique une géométrie de coordonnées et on travaille sur la « propriété spécifique » d'une courbe, ce que nous nommons « équation ». La recherche d'une tangente sera celle de la position limite d'une sécante lorsque les points d'intersection avec la courbe tendent à se rapprocher et on quantifiera les calculs en termes d'infiniment petits, qui seront cette fois numériques plus que géométriques. Le procédé d'« adégalisation » cher à Fermat fera plus que les faire tendre vers 0 puisqu'il les annulera purement et simplement après les simplifications d'usage du calcul !
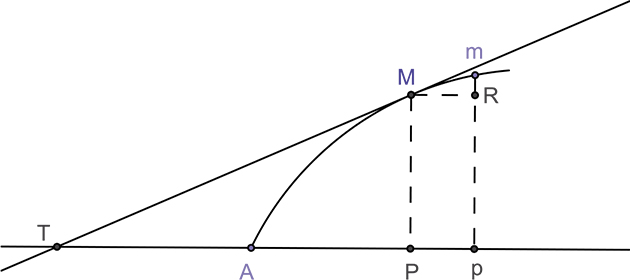Vient ensuite le calcul différentiel, initié par Gottfried Wilhelm Leibniz (1646-1716), popularisé en 1696 par le marquis de L'Hospital dans son Analyse des infiniment petits pour l'intelligence des lignes courbes : « Soit une ligne courbe AM telle que la relation de la coupée [abscisse] AP à l'appliquée [ordonnée] PM soit exprimée par une équation quelconque, et qu'il faille du point M sur cette courbe mener la tangente MT. […] On concevra une autre appliquée mp infiniment proche de la première avec une petite droite MR parallèle à AP. » Quelques calculs plus loin, faisant intervenir y = PM, Pp = MR = dx et Rm = dy, les triangles mRM et MPT étant semblables, on obtient dy / dx = y / PT, on en déduira « une valeur de la sous-tangente PT en termes entièrement connus […] laquelle servira à mener la tangente cherchée MT. »
Isaac Newton (1642-1727) a lui aussi une approche mécanique de la tangente, et met la notion de limite au cœur de l'analyse, l'obtenant comme on le ferait d'une vitesse instantanée. On arrive donc à la notion de dérivée par l'intermédiaire de celle de vitesse, à l'inverse de ce que feront Leonhard Euler (1707-1783) et Augustin Louis Cauchy (1789-1857), qui partiront de la dérivée pour introduire la vitesse.
On arrive donc à la fin du XVIIIe siècle à une définition rigoureuse du nombre dérivé par Jean Le Rond D'Alembert (1717-1783), la notion de dérivée étant véritablement formalisée par Karl Weierstrass (1815-1897), ce qui fournira à la tangente à une courbe son équation.
De la tangente à l'asymptote
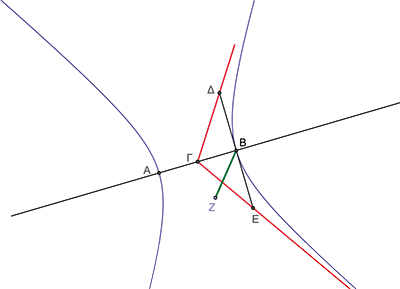
Les géomètres de l'Antiquité, comme Apollonius, s'étaient déjà penchés longuement sur la question. Ce dernier a par exemple étudié abondamment le sujet dans le Livre II de son traité les Coniques, où il explique par exemple que, étant donnée une hyperbole H de centre Γ, de diamètre AB, et de « côté droit » (la demi-corde focale) matérialisé par BZ, avec AB = d et BZ = c, si, sur la tangente en B on porte les longueurs
alors les droites (ΓΔ) et (ΓE) ne rencontrent pas H. Il en fait la démonstration par l'absurde.
En utilisant la « géométrie de coordonnées » chère à Descartes, on dit aujourd'hui, pour la courbe représentative d'une fonction f, qu'elle admet la droite d'équation y = ax + b pour asymptote (oblique si a ≠ 0) si
qu'il s'agisse de
Lire la suite