Céviennes et ménéliennes

Une cévienne (autrement dit « droite de Céva ») est une droite qui passe par l'un des sommets d'un triangle. Son nom est bien sûr lié à celui du mathématicien italien Giovanni Ceva, qui a démontré en 1678 le théorème qui porte son nom.

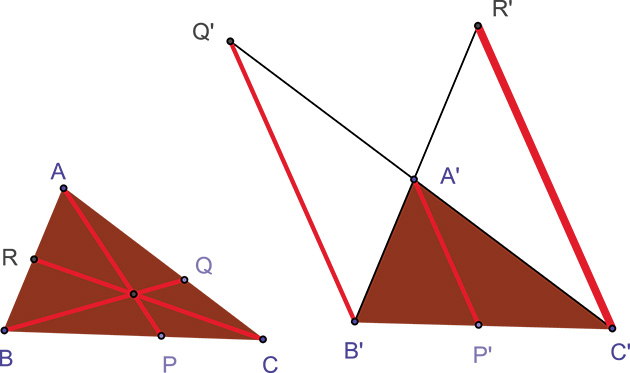
Dans un triangle ABC, pour trois points P, Q, R différents des sommets A, B et C, situés respectivement sur les droites (BC), (CA) et (AB), les céviennes (AP), (BQ) et (CR) sont concourantes ou parallèles si, et seulement si, 

(la notation  signifie que l'on considère la mesure algébrique de la distance entre P et B).

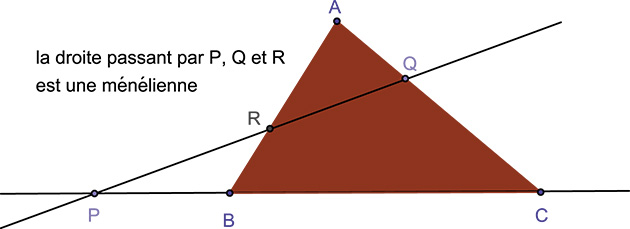
Une ménélienne (pour « droite de Ménélaüs ») est une droite qui rencontre les trois côtés (éventuellement prolongés) d'un triangle ABC. Si elle porte ce nom, c'est évidemment en référence au théorème de Ménélaüs (fin du 1^er siècle) : soient, sur les côtés d'un triangle ABC, trois points P, Q et R. Une condition nécessaire et suffisante pour qu'ils soient alignés est que 

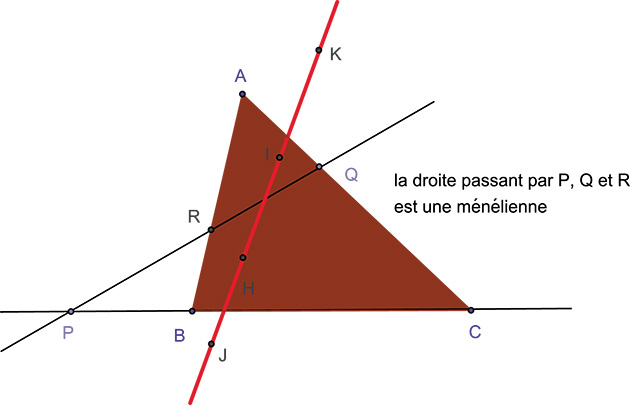
Voici maintenant un joli résultat, que Jacob Steiner a lui-même proposé parmi une liste de questions dans les Annales de Gergonne en 1828 : les orthocentres respectifs I, J, K et H des triangles ARQ, BPR, CPQ et ABC sont alignés !

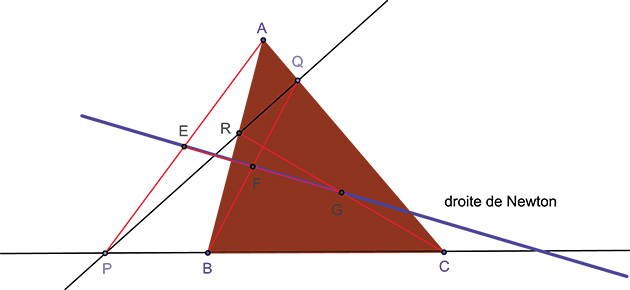
La droite de Newton

Le triangle ABC et la ménélienne passant par P, R, Q (voir ci-contre) permettent de définir un quadrilatère complet BCQR (complet car caractérisé par quatre droites se coupant deux à deux en six points). Les milieux respectifs E, F et G des diagonales [AP], [BQ] et [CR] de ce quadrilatère sont alignés. C'est dans lesPrincipia de Newton, recueil de théorèmes purement géométriques sur les coniques, que l'on trouve en particulier cet alignement, à qui Jacob Steiner donna le nom de droite de Newton. Gauss, en 1810, redécouvre cette droite, si bien qu'on l'appelle parfois aussi droite de Gauss.

La droite et le point de Lemoine

Mathématicien pour le plaisir, Émile Lemoine lance la géométrographie. On retrouve dans son ouvrage de 1873 Sur quelques propriétés d'un point remarquable du triangle tout son art de la construction géométrique, dont le point vedette est précisément le point de Lemoine. Défini comme l'intersection des symédianes (symétriques des médianes par rapports aux bissectrices intérieures) d'un  triangle, on peut en faire une construction moins exigeante en tracés. À partir du triangle tangentiel UVW, on démontre que les symédianes ne sont autres que les droites (AU), (BV) et (CW) et qu'elles se coupent en L, le fameux point de Lemoine du triangle ABC.

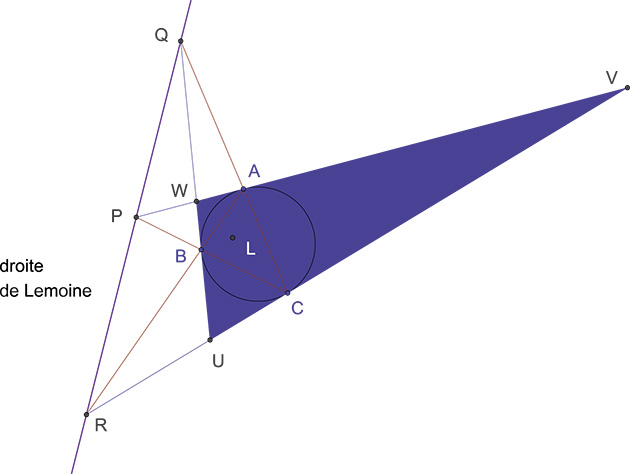
Il y a même plus : si les côtés du triangle UVW (éventuellement prolongés) coupent ceux de ABC en P, Q et R, alors ces derniers sont alignés sur… la droite de Lemoine du triangle ABC.