Ouvrons, avec les faisceaux de droites, thème un peu désuet qui n'est plus ni enseigné ni beaucoup pratiqué, une séquence « nostalgie » : il ne s'agirait pas d'oublier que cette notion de géométrie affine, que l'on peut interpréter en géométrie analytique, peut être constructive et amener à des simplifications bienvenues.

Desargues : innovation et modernité

Moins connu que d'autres géomètres comme Pascal ou Descartes, Girard Desargues (1591-1661) a eu de la géométrie une approche innovante. Il a su, en 1639, dans son Brouillon project d'une atteinte aux événemens des rencontres d'un cône avec un plan, un opuscule de trente pages seulement, définir une « ordonnance de lignes droites » comme une famille de droites soit toutes concourantes en un point, soit toutes parallèles : les faisceaux de droites étaient nés. Desargues est même allé assez loin dans la modernité en introduisant un point à l'infini pour chaque droite et le traite sans le distinguer des points à distance finie, mettant en place de facto la géométrie projective.

En géométrie affine plane, on distinguera donc les faisceaux de droites concourantes, ensemble de droites se coupant toutes en un même point, des faisceaux de droites parallèles, ensemble de droites toutes parallèles entre elles. Pour définir un faisceau , deux droites d₁ et d₂ suffisent : si elles se coupent, les autres droites de passent par le point d'intersection ; si elles sont parallèles, les autres droites de F leur seront parallèles aussi.

Les définitions géométriques sont claires, et pourtant, comment faire concrètement pour prouver que des droites sont en faisceau ? C'est là que la géométrie analytique chère à Descartes, c'est-à-dire la géométrie dans un repère, nous est d'un grand secours.

Pour définir un faisceau, deux droites suffisent : d₁, d'équation ax + by + c = 0 dans un certain repère du plan ou, en posant D₁ = ax + by + c, d'équation D₁ = 0. Puis d₂, d'équation a'x + b'y + c' = 0 ou, en posant D₂ = a'x + b'y + c', d'équation D₂ = 0.

La famille de droites d d'équations respectives D= , où et sont deux paramètres, est précisément le faisceau que définissent D₁ et D₂. En effet :

• dire que d₁ et d₂ se coupent en un point P équivaut, en remplaçant, dans D₁ et D₂, x et y par les coordonnées de P, à D₁ = D₂ = 0, soit , ou D = 0. C'est donc que d passe aussi par P ;

• dire que d₁ et d₂ sont parallèles équivaut à dire que ab' – ba' = 0. Comme dans l'équation les coefficients de x et de y sont respectivement et , et si on calcule
on trouve bien 0. C'est donc que d est parallèle à d₁ et à d₂.

C'est que l'on appellera l'équation du faisceau déterminé par d₁ et d₂ et il sera souvent plus facile de l'utiliser pour prouver qu'une droite d appartient à un faisceau que de se fier à la seule géométrie : cela reviendra à vérifier que le premier membre de l'équation de d est combinaison linéaire de D₁ et D₂.

Un outil puissant

Le détour par un faisceau de droites peut s'avérer intéressant, facilitant les démonstrations. Voici un exemple de cette « économie » : ABCD est un parallélogramme dont les côtés (ou les droites qui les portent) sont coupés par deux droites passant par un point M, (EF) parallèle à (AB) et (GH) parallèle à (BC), comme sur le dessin. Il s'agit de prouver que les droites (AC), (FG) et (EH) se coupent en un même point I.

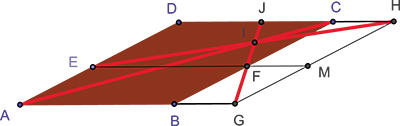
Si (AC) et (FG) se coupent en I, on va montrer que (EH) passe aussi par I. Une première méthode, purement géométrique mais un peu sophistiquée, fait intervenir deux homothéties : h₁, de centre I, qui transforme F en G et h2, de centre I, qui transforme A en C. Les homothéties h₂ o h₁ et h₁ o h₂, toutes deux de centre I et de rapport le produit de ceux de h₁ et de h₂, sont une seule et même transformation h, de centre I, qui transforme (AD) (par h₂) en (BC) puis (BC) en (GH) par h₁. Elle transforme aussi (EF) en (AB) (par h₁) puis (AB) en (CD) (par h₂), si bien que, par intersections, h transforme E en H. C'est donc que (EH) passe aussi par I.

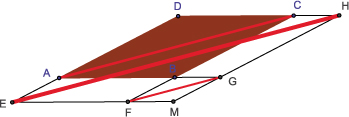
Une seconde méthode, plus expéditive, utilisera le repère . Dans ce repère, l'équation de la droite (AC) est D = x – y = 0 et, si le point M a pour coordonnées (a, b), l'équation de la droite (FG) est D₁ = bx + (a – 1) y – ab = 0, celle de (EH) est D₂ = (b – 1) x + ay – ab = 0. Comme D₁ – D₂ = D, c'est que les droites (AC), (FG) et (EH) forment un faisceau. Là, inutile de considérer, comme précédemment, deux cas ; on obtient immédiatement que les droites (AC), (FG) et (EH) sont ou toutes trois concourantes ou toutes trois parallèles. La théorie des faisceaux de droites est donc un outil de démonstration puissant. Pourquoi s'en passer ?