Si l'on efface une courbe plane après avoir tracé un grand nombre de ses tangentes, la figure obtenue « garde le souvenir » de la courbe originelle comme enveloppe de l'ensemble des droites. Plus généralement, pour une famille de courbes à un paramètre d'équation f (x, y, \( \lambda\) ) = 0, l'enveloppe est une courbe tangente à chacune des courbes de cette famille. La détermination des enveloppes est l'un des grands problèmes de la géométrie différentielle, qui revient à résoudre le système : 

\( \left\{ \begin{array}{l} f(x,y, \lambda)=0\\ \frac{\partial f}{\partial \lambda}(x,y, \lambda)=0 \end{array} \right.\)

Sa résolution fournit dans le cas général une solution paramétrée

\( \left\{ \begin{array}{l} x=u(\lambda)\\ y=v(\lambda) \end{array} \right.\)

et, si l'on arrive à éliminer le paramètre \( \lambda\) , une solution implicite g (x, y) = 0.

Savoir prendre la tangente

Des enveloppes de solutions régulières peuvent apparaître comme solutions singulières d'équations différentielles. Prenons l'exemple d'une famille (F) de cercles de rayon R centrés sur l'axe des abscisses. Leur équation est \( (x-\lambda)^2+y^2=R^2\) . En dérivant cette équation par rapport à x, on obtient la relation \( (x-\lambda)+yy'=0\) , ce qui conduit à l'équation différentielle y² (y'² + 1) = R² vérifiée par cette famille de cercles. Outre les solutions circulaires régulières, on voit apparaître des solutions singulières à notre problème, les solutions constantes y = ± R, qui sont bien tangentes à tout cercle de cette famille (F)

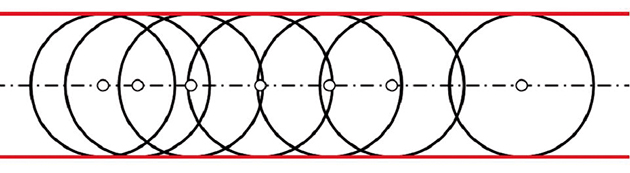
Dans le cas particulier où les courbes enveloppantes sont des droites, l'équation familiale est de la forme \( a(\lambda)x+b(\lambda)y+c(\lambda)=0\) . La seconde équation du système, \( a'(\lambda)x+b'(\lambda)y+c'(\lambda)=0,\) où les dérivées sont prises par rapport au paramètre \( \lambda\) , est alors elle aussi l'équation d'une famille de droites. Le système linéaire à résoudre fait donc apparaître le point courant de l'enveloppe comme l'intersection de deux droites, ce qui peut en permettre une construction, comme l'illustre le cas des coniques.

Les coniques sont les enveloppes d'une famille de droites. Ces droites sont les médiatrices d'un segment dont une extrémité est un foyer et dont l'autre extrémité décrit un cercle centré sur l'autre foyer (pour le cas parabolique, l'un des foyers doit être considéré comme étant à l'infini).

Soient F₁ et F₂ les foyers de la conique à construire et (C₁) le cercle de centre F₁ et de rayon R = 2a (voir la figure). En prenant pour centre du repère cartésien le milieu O des foyers tel que OF₁ = OF₂ = c, un point courant P du cercle (C₁) a pour coordonnées \( (R \cos(\alpha)-c, R\sin(\alpha))\) . D'après le théorème de Thalès, le milieu I du segment F₂P a pour coordonnées \( (a \cos(\alpha), a\sin(\alpha))\)   puisque OI = R/2 = a. Le point I appartient donc toujours au cercle (C₂), image du cercle (C₁) par l'homothétie de centre F₂ et de rapport 1/2. Puisque le vecteur  \( \) \( \overrightarrow{F_2P}\) a pour coordonnées \( (R \cos(\alpha)-2c, R\sin(\alpha))\) , la médiatrice (D) du segment [F₂P], passant par le point I, a pour coefficient directeur  \( p = (c – a \cos (\alpha) / a \sin (\alpha))\) et pour équation :

\( \) \( x(a \cos(\alpha)-c+ay\sin(\alpha)+ca\cos(\alpha)-a^2=0.\)

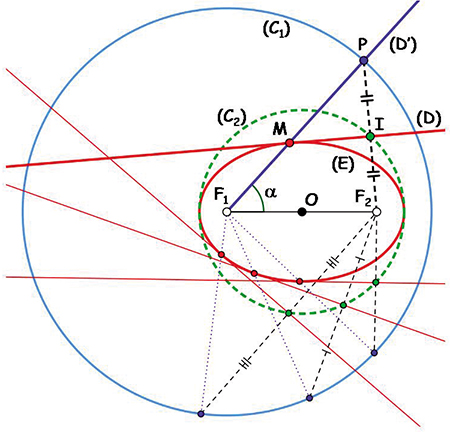Il faut alors dériver cette équation par rapport au paramètre angulaire \( \alpha\)   pour obtenir la seconde équation (D') du système. Après simplification, on obtient \( y=(x+c)\tan(\alpha)\) , qui n'est autre que l'équation de la droite (F₁P). Ainsi, la droite (D), obtenue par le pliage amenant le point P sur le foyer F₂, est une tangente de l'ellipse (E), mais en outre son intersection avec la droite (F₁P) détermine le point M de tangence avec l'ellipse (E).

Le même type de construction est encore valable pour une hyperbole avec, dans ce cas, le foyer F₂ hors du cercle (C₁), c'est-à-dire a < c.

Pour la parabole, il suffit de considérer le second foyer à l'infini pour obtenir une construction en tous points similaire à celles de l'ellipse et de l'hyperbole. Les cercles (C₁) et (C₂) deviennent des droites, toujours images l'une de l'autre par une homothétie de centre F et de rapport 1/2.

Sous des caustiques

Propriétaire d'une verrerie où il fabriquait des lentilles « d'une grandeur qu'on avait point encore vue », le physicien allemand Ehrenfried Walther von Tschirnhaus fut le premier à étudier d'un point de vue géométrique les enveloppes des rayons réfléchis par des surfaces, qu'il nomma caustiques, du grec katein (brûler). Sa première étude, en 1682, concerne la caustique « au soleil » (source lumineuse à l'infini) d'un cercle : la néphroïde, nommée ainsi pour sa ressemblance à un rein. La réflexion d'un rayon incident en un point P du cercle (C₁) de rayon R est la droite (D) symétrique par rapport au rayon vecteur \( \overrightarrow{OP}\) . Un peu de géométrie élémentaire montre que la droite (D) forme un angle 2 \( \alpha\) avec la direction des rayons incidents, d'où son équation,

\( x \sin(2\alpha)-y\cos(2\alpha)=R\sin(\alpha).\)

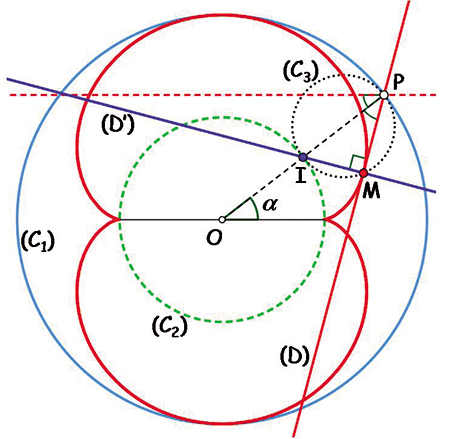En la dérivant par rapport au paramètre \( \alpha\) , on trouve l'équation de la droite (D') :

\( x \cos(2\alpha)+y\sin(2\alpha)=R\cos(\alpha)/2,\)

qui est perpendiculaire à (D). La résolution du système constitué des équations des droites (D) et (D') donne bien sûr les coordonnées paramétrées du point M de la néphroïde, mais on peut aussi en déduire une méthode constructive. Le segment [OP] est constitué de points de coordonnées \( (r \cos(\alpha), r\sin(\alpha))\) . L'intersection des droites (D') et (OP) est alors le point I tel que r = R / 2, qui appartient au cercle (C₂), et même au cercle (C₃) de diamètre IP, puisque les droites (D) et (D') sont perpendiculaires. Ces deux cercles étant tangents en I, on retrouve le fait que la néphroïde est une épicycloïde à deux points de rebroussement, en tant que trajectoire d'un point du cercle (C₃) roulant sans glisser sur le cercle (C₂), de rayon double.

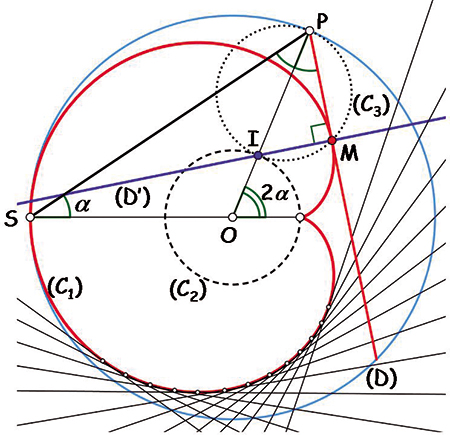\( \alpha\) et son équation est alors

\( x\sin(3\alpha)-y\cos(3\alpha)=R\sin(\alpha).\)
 

On en déduit l'équation, \( x\cos(3\alpha)+y\sin(3\alpha)=R\cos(\alpha)/3\) , de la droite (D') qui intercepte, cette fois-ci, le rayon  \( \overrightarrow{OP}\) au point I du cercle (C₂) et de rayon R / 3. Les cercles (C₂) et (C₃) ayant même rayon, la cardioïde est donc une épicycloïde à un point de rebroussement.

Et si vous continuez cette marche au flambeau en cherchant la caustique par réflexion (ou catacaustique) d'une cardioïde avec un point lumineux en son point de rebroussement, vous retrouvez… une néphroïde !