Peut-on imaginer figure plus simple qu'un triangle ? Et pourtant, on ne se rend pas toujours compte de là où peuvent nous mener trois inoffensifs points dans un plan. Les droites remarquables du triangle ne manquent déjà pas de nous étonner. Les trois médiatrices (les perpendiculaires à chaque côté et passant par leurs milieux) sont concourantes, les trois médianes (qui passent par le milieu d'un côté et par le sommet opposé) le sont aussi, et les trois hauteurs (droites passant par un sommet et perpendiculaires au côté opposé) également. On définit ainsi le centre O du cercle circonscrit, le centre de gravité G et l'orthocentre H du triangle. Il n'en faut pas plus pour obtenir le plus célèbre des théorèmes d'alignement : O, G et H sont sur une seule et même droite, la droite d'Euler (voir en page 24). Plus remarquable encore, ces trois points sont toujours alignés dans cet ordre et OH = 3 OG.

 
Des points, des cercles et des quadrilatères

Les pieds des hauteurs, les milieux des segments reliant les côtés à l'orthocentre et les milieux des côtés du triangle sont tous sur un même cercle, dit cercle de Feuerbach (voir le Cercle, Bibliothèque Tangente 36, 2009). Et le centre  de ce cercle, dont le rayon est deux fois plus petit que celui du cercle circonscrit, se trouve… sur la droite d'Euler, au milieu de [OH].

Robert Simson connaissait déjà l'existence de la droite d'Euler. Ce sont deux brillants géomètres français, Jean-Victor Poncelet et Charles-Julien Brianchon, qui mettront en évidence le cercle de Feuerbach en 1821. Mais l'histoire de s'est pas arrêtée là et nombreux sont ceux qui, à l'instar d'Olry Terquem, ont découvert que d'autres points remarquables se trouvaient sur ce cercle.

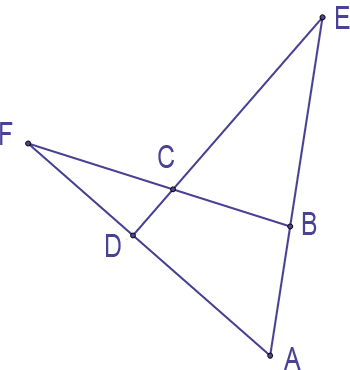Un quadrilatèrecomplet.

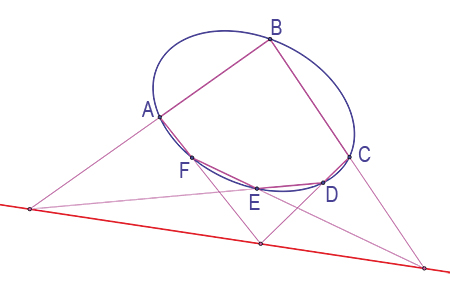
Vous voyez certainement ce qu'est un quadrilatère, mais connaissez vous le quadrilatère complet ? Rien de bien compliqué, il suffit de prendre un quadrilatère ABCD et de lui ajouter les intersections des droites portées par les côtés opposés. On obtient alors la figure ci-contre.  

Cet objet cache bien des surprises lui aussi. Il possède trois diagonales, (AC), (BD) et (EF), dont les milieux sont alignés sur la droite de Newton (voir en page 22). Mais si l'on note M le second point d'intersection des cercles circonscrits à AED et ABF, ce sont les quatre projetés orthogonaux de M sur les côtés du quadrilatère complet qui sont alignés !

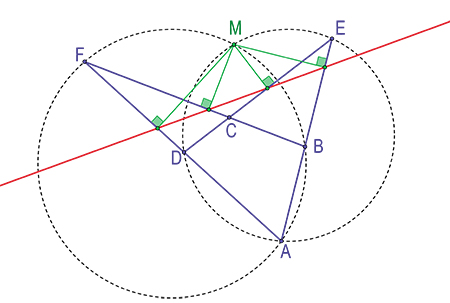 Nouveau coup de théâtre, les orthocentres des quatre triangles formés par les côtés d'un quadrilatère complet sont eux aussi alignés !

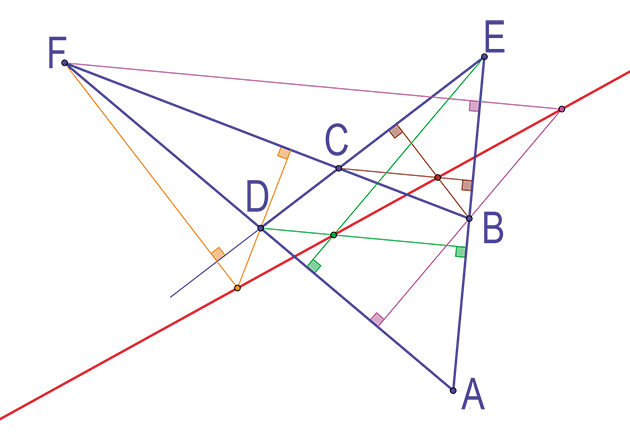 Et si ABCD est un trapèze ? Difficile de construire un quadrilatère complet dans ce cas, mais le trapèze complet est aussi source d'étonnement. En effet, ici encore, quatre points remarquables sont alignés : l'intersection des diagonales, les milieux des bases et l'intersection des droites portées par les deux autres côtés.

Le trapèze complet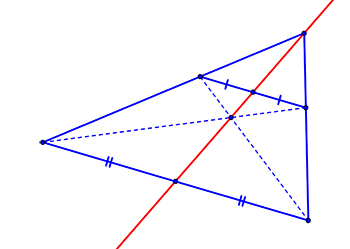Avec des droites et des coniques

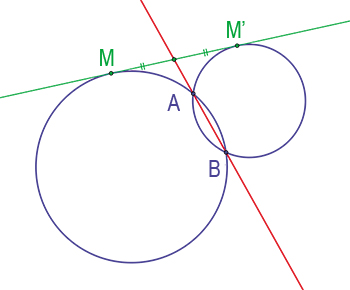
Le théorème de l'axe radical

En 1640, alors qu'il n'est âgé que de 16 ans, Blaise Pascal publie un Essay pour les coniques dans lequel figure une démonstration d'un théorème d'alignement devenu célèbre et nommé alors hexagramme mystique (voir Tangente SUP 48, 2009). L'ouvrage est d'une qualité si rare que René Descartes croit d'abord à une erreur d'attribution et pense que cette publication est du père de l'auteur des Pensées, Étienne Pascal, qui fréquentait alors assidûment les cercles scientifiques de son époque avec Mersenne et Roberval !

Considérons donc maintenant une conique, c'est-à-dire une courbe obtenue par section d'un cône. Il peut s'agir d'un cercle, d'une ellipse, d'une parabole ou encore d'une hyperbole. Si ABCDEF est un hexagone inscrit dans cette conique, alors les points d'intersection des droites portées par ses côtés opposés sont alignés.

La géométrie projective est le contexte idéal des questions d'alignement. On peut facilement y démontrer deux célèbres résultats dont la saveur toute particulière est justement due au fait que seules les notions d'alignement de points et d'intersections de droites y interviennent.

Le théorème de Pappus indique ainsi que, si A, B, C sont alignés et si D, E, F le sont aussi, alors les points M, N et P intersections respectives de (AE) et (BD), (AF) et (CD) et enfin (BF) et (CE) sont encore alignés.

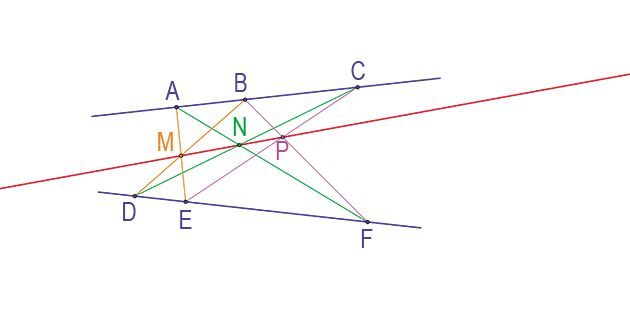 Le théorème de Pappus

Le théorème de Desargues affirme quant à lui que si (AA'), (BB') et (CC') sont trois droites concourantes, alors les points M, N et P, intersections respectives de (AB) et (A'B'), (AC) et (A'C') et enfin (BC) et (B'C') sont alignés.

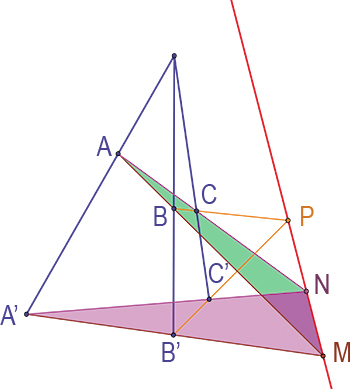 Le théorème de Desargues, limpide si l'on considère la figure comme étant une représentation des plans sécants (ABC) et (A'B'C').

Un autre célèbre problème ne fait référence qu'à des questions d'alignement : le problème de Sylvester. En 1893, James Joseph Sylvester, éminent géomètre britannique, propose cette énigme qu'il n'a pas réussi à résoudre lui-même. La question consiste à montrer que tout ensemble fini E de points du plan tel que toute droite contenant deux points de E en contient un troisième est en fait constitué de points tous alignés sur une même droite. C'est au Hongrois Tibor Gallai, spécialiste de théorie des graphes, que l'on doit la première démonstration, quelques décennies après l'énoncé du problème. Elle utilise la notion de distance (voir en encadré). D'autres démonstrations, plus difficiles mais ne faisant appel qu'à des notions d'incidence « pures », ont été trouvées ensuite. Les questions d'alignement sont simples à exprimer mais pour les justifier, il est parfois difficile d'aller… droit au but !