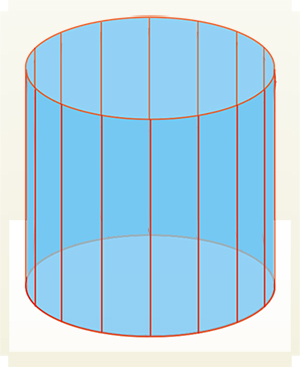
Imaginez que l'on cherche à construire une surface… à partir de droites. La première surface réglée qui vienne à l'esprit quand on veut échapper au plan est le cylindre, une sorte de plan enroulé. On peut le construire également à partir de deux roues montées sur un même axe métallique, en tendant des élastiques entre elles.

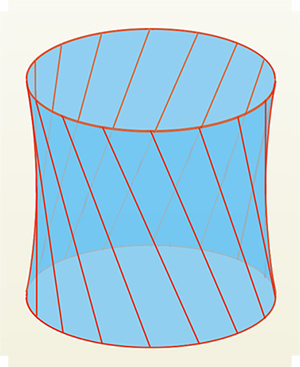Il suffit de tourner l'une des roues, celle du dessus par exemple, pour obtenir un objet plus surprenant. Les élastiques se déplacent et une nouvelle surface apparaît. Elle porte le nom compliqué d'hyperboloïde de révolution à une nappe. Son équation dans un repère orthonormé bien choisi est de la forme x² + y² – k² z² = 1 où k > 0 (l'axe (Oz) est donc l'axe des roues et l'unité a été choisie pour simplifier l'équation).

Pourquoi un tel nom ? Tout simplement parce qu'on l'obtient également en faisant tourner une hyperbole autour de l'un de ses axes. Si on fait tourner la même hyperbole autour de son autre axe, on obtient une surface en deux parties, ou deux nappes. Pour distinguer ces deux surfaces très différentes, on précise toujours le nombre de nappes.

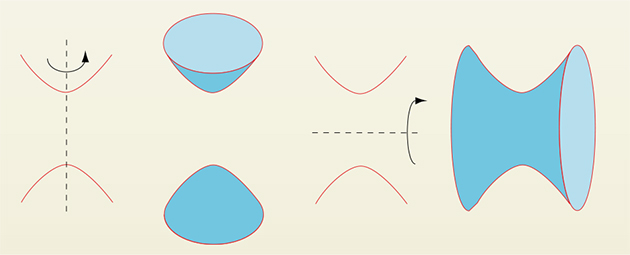
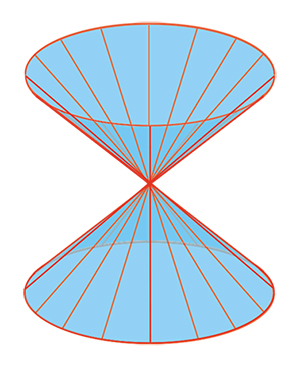Par construction, ces surfaces sont de révolution autour de l'axe des roues, et engendrées par des droites (les élastiques), que l'on nomme génératrices pour cette raison. Tordez maintenant le cylindre dans l'autre sens. Vous obtenez la même surface, qui est ainsi pourvue de deux familles de génératrices ! Cette propriété assure sa rigidité si on la construit avec des tiges indéformables fixées aux deux cercles du départ.

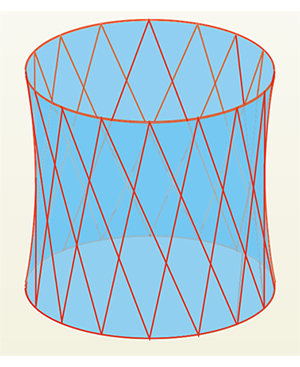Cette surface se retrouve fréquemment dans le paysage car, pour des raisons physiques, les tours de refroidissement des centrales thermiques ou nucléaires adoptent cette forme. On l'utilise aussi pour construire des châteaux d'eau. Les deux familles de génératrices ont un avantage en architecture : elles simplifient le ferraillage du béton armé. Les deux familles permettent d'ailleurs que la ferraille tienne debout seule.

Au Népal, les tabourets traditionnels sont fabriqués avec des morceaux de bambous de même longueur, liés par des cordes en plusieurs endroits, et décalés du même angle, dans un sens comme dans l'autre, si bien que l'on obtient un hyperboloïde de révolution.

Des toits originaux

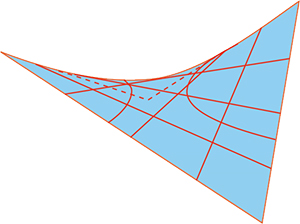La méthode utilisée pour construire l'hyperboloïde peut être reproduite en remplaçant le cylindre par un plan. Autrement dit, on garde le dispositif initial, axe et roues, mais, au lieu de tendre les élastiques entre les deux roues, on les tend entre deux rayons parallèles, avant de tourner les roues. On obtient une nouvelle surface admettant deux familles de droites génératrices comme la précédente. Elle porte le nom de paraboloïde hyperbolique, car on peut y voir des paraboles et des hyperboles. Pour les mêmes raisons, cette nouvelle surface est également utilisée en architecture. Elle sert notamment à fabriquer des toits. Dans un repère orthonormé bien choisi, cette surface a pour équation xy = kz.

Les surfaces réglées précédentes sont toutes des quadriques, c'est-à-dire qu'elles ont des équations de degré deux. Ce sont les plus utilisées dans la pratique. Bien entendu, il en existe de degrés supérieurs, par exemple les hélicoïdes, utilisés dans les rampes d'accès de certains parkings souterrains. On peut en admirer une réalisation plus esthétique dans la tour cavalière du château d'Amboise, une sorte d'escalier en colimaçon… sans les marches.

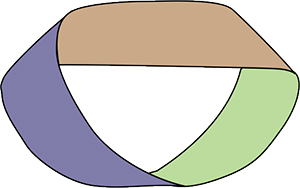
Le ruban de Möbius est également une surface réglée ! Pour l'obtenir, on commence par enrouler une bande de papier, comme pour former un cylindre, mais on la tourne d'un demi-tour avant de la coller pour obtenir une surface naturellement réglée mais… ne possédant qu'une face !