Les mathématiques, telles que nous les connaissons aujourd'hui, sont universelles. Elles peuvent être comprises par tous de la même manière : les vérités qu'elles véhiculent ne sont pas fondées sur des récits personnels ni révélées, mais sont toutes prouvées à l'aide de démonstrations dont les règles de construction sont précises et peuvent être comprises de tous. En ce sens, les mathématiques sont démocratiques ! L'apparition des démonstrations va d'ailleurs de pair avec celle de la démocratie en Grèce antique.

Un apport décisif dans cette direction se trouve dans les Éléments d'Euclide.

Un mystérieux encyclopédiste didacticien

Euclide a eu une très grande influence sur les mathématiques en général, et sur la géométrie en particulier : la géométrie de base que l'on enseigne encore aujourd'hui lui est redevable. Et pourtant, cet auteur est assez méconnu : on ignore presque tout de sa famille, de son éducation, de ses maîtres… On ne connaît même pas de façon précise sa ville d'origine, ni ses dates de naissance et de mort. En fait, les seuls renseignements connus à propos de sa vie proviennent de commentaires sur son œuvre. Certains de ses successeurs l'appellent Euclide d'Alexandrie. Proclus (412– 485) a signalé, dans un commentaire des Éléments, qu'Euclide connaissait des travaux d'Eudoxe (environ – 408 ; environ – 355) et de Théétète d'Athènes (environ – 415 ; environ – 369), mais qu'il était « plus ancien » qu'Archimède (environ – 287 ; – 212) et qu'Ératosthène (environ – 276 ; – 194). Avec de tels renseignements, on peut estimer qu'Euclide est né vers – 330 et mort vers – 275. Ces dates restent très incertaines.

copyright : m@ths et tiques (www.maths-et-tiques.fr)

En outre, certains écrivains ont émis des doutes à propos de l'existence même du mathématicien ! En effet, certains historiens du Moyen Âge pensaient que le personnage était purement mythique et symbolisait les mathématiques grecques (son nom se compose des deux mots grecs  et  , qui signifient respectivement « la clef » et « le nombre 2 », qui, pour les pythagoriciens, faisait référence à la droite et par extension à la géométrie).

Enfin, des scientifiques contemporains ont observé des différences de style dans les écrits attribués à Euclide ; ils ont émis l'hypothèse qu'il n'y aurait pas un seul auteur, mais bien un collectif, qui fait un peu penser à ce que l'on a connu récemment avec Bourbaki.

Le mystère reste donc entier. Quoi qu'il en soit, ce qu'il faut retenir d'Euclide ce sont ses publications, multiples et variées. Elles concernent l'astronomie, la mécanique, la musique, l'optique, et bien entendu les mathématiques, avec plusieurs ouvrages de géométrie. Le plus célèbre est un recueil de treize Livres intitulé les Éléments ; d'ailleurs, les Anciens surnommaient Euclide le Stoicheiôtês, ce qui signifie précisément « l'auteur des Éléments ».

Les Éléments constituent une sorte d'encyclopédie qui rassemble les connaissances de l'époque en géométrie (du plan et de l'espace) et en arithmétique. Cette œuvre se distingue par son exposé synthétique et sa construction didactique sous forme déductive. Elle présente les objets et leurs relations en allant systématiquement du plus simple vers le plus compliqué : en partant de définitions et d'hypothèses explicitement admises, des propriétés sont démontrées par déduction logique en exploitant uniquement des principes ou des acquis antérieurs. Ainsi, elle a servi de modèle pour les générations suivantes en mettant en avant la « démarche hypothético-déductive » qui est utilisée de nos jours en mathématiques. Elle a été traduite dans la plupart des langues anciennes ou modernes, au départ de l'édition originale en grec (évidemment perdue).

Un concept qui ne va pas forcément de soi

Comme Euclide a visiblement opté pour une construction progressive de ses Éléments en étant rigoureux (pour l'époque), les objets géométriques (abstraits) de base sont introduits dans le Livre I. Celui-ci se compose de vingt-trois définitions (qui précisent les objets étudiés, ainsi que certaines de leurs propriétés : angles, triangles, carrés, cercles, perpendiculaires, parallèles, diamètres…) ; cinq demandes ou postulats (vérités géométriques admises a priori) ; neuf notions communes ou axiomes (des évidences, également admises sans preuve, qui déterminent l'usage des égalités et inégalités d'une manière générale) ; quarante-huit propositions ou propriétés des objets définis (démontrées à partir des postulats, axiomes et résultats antérieurs).

Euclide n'avait pas pris le parti d'introduire le concept de droite en se basant sur une expérience du monde sensible. Il cherchait à présenter les objets étudiés de manière abstraite, « en partant de rien ». C'est pourquoi il ne considérait pas de suite le concept, pourtant fondamental en géométrie, de droite.

L'ouvrage de référence Éléments d'Euclide (volume 1, Livres I–IV), traduit et commenté par Bernard Vitrac (Presses universitaires de France, 1990) commence par l'introduction de trois concepts primitifs :

Définition 1. « Un point est ce dont il n'y a aucune partie. »

Définition 2. « Une ligne est une longueur sans largeur. »

Définition 3. « Les limites d'une ligne sont des points. »

Si ces formulations peuvent paraître floues et abstraites, l'ensemble est toutefois cohérent. Par exemple, la première définition est essentiellement « négative » car elle ne peut pas faire appel à des notions ultérieures.

À ce stade, une ligne désigne aussi bien une courbe qu'une portion de courbe. Elle est donc bornée ou non, et peut être rectiligne ou incurvée. C'est dans la définition suivante que l'auteur introduit le type de ligne qui nous intéresse :

Définition 4. « Une ligne droite est celle qui est placée de manière égale par rapport aux points qui sont sur elle. »

Cette présentation de la droite a suscité de nombreuses interprétations dans des commentaires (notamment par Proclus) de l'œuvre. Visiblement, Euclide évitait de recourir à une approche intuitive ou matérielle de la « rectitude ». Il ne faisait donc pas référence à la représentation (tactile) d'une droite comme idéalisation d'un fil tendu (ce qui semblait connu depuis Platon), ni à celle, visuelle, de la trajectoire d'un rayon lumineux (idée qu'il développe pourtant dans un ouvrage consacré à l'optique).

Il ne pouvait pas non plus définir la droite de façon géodésique (comme le fera son successeur Archimède), comme ligne la plus courte entre deux de ses points : en effet, le concept de distance n'était pas encore introduit !

Selon certains historiens contemporains, l'auteur avait en vue l'« homéomérie », c'est-à-dire la possibilité d'amener n'importe quelle partie de la ligne en coïncidence avec toute autre partie. Cependant, cette propriété n'est pas caractéristique d'une droite : elle est aussi vérifiée par le cercle et certaines spirales. Toujours est-il qu'Euclide éprouvait le besoin de préciser et compléter cette Définition 4 au moyen de trois demandes :

Demande 1.  Qu'il soit demandé de mener une ligne droite de tout point à tout point. »

Demande 2. « Et de prolonger continûment en ligne droite une ligne droite limitée. »

Demande 5.  « Et que, si une droite tombant sur deux droites fait les angles intérieurs et du même côté plus petits que deux droits, les deux droites, indéfiniment prolongées, se rencontrent du côté où sont les angles plus petits que deux droits. »

La première demande garantit l'existence, et aussi, d'après Proclus, l'unicité d'une droite passant par deux points ; elle est parfois énoncée sous cette forme plus commode :

Postulat 1 : Par deux points distincts, il passe une droite et une seule.

La deuxième demande permet de prolonger un segment de droite (qui peut être une ligne au vu de ce qui précède) au-delà de ses deux extrémités. Elle peut s'énoncer de façon équivalente comme suit :

Postulat 2 : Tout segment est prolongeable en une droite.

Après deux demandes intermédiaires permettant de tracer un cercle (demande 3) ou garantissant l'égalité des angles droits (demande 4), la cinquième et dernière demande traite de positions relatives de droites. Le mathématicien britannique John Playfair l'a exprimée, en 1795, sous cette forme équivalente, qui est le plus souvent utilisée :

Postulat 5 : Par un point extérieur à une droite D, il passe une droite et une seule parallèle à D.

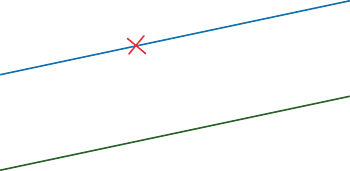
De nombreux mathématiciens se sont efforcés en vain de démontrer ce cinquième postulat à l'aide des quatre premiers. On sait désormais que ceci est impossible : le postulat peut être nié, ce qui donne alors naissance à d'autres géométries que celle d'Euclide.