Il existe depuis toujours des compétitions d'athlétisme ou de ski pour filles, il y a depuis 1927 des compétitions d'échecs pour les filles... Alors, pourquoi ne pas envisager des compétitions de maths au féminin ? Faisons le point sur les initiatives existantes.

Partant du constat que les filles participent peu aux compétitions mathématiques (la participation à l'Olympiade internationale de mathématiques plafonne à 11 %, tous pays confondus) et sont peu attirées par les études scientifiques en général, mathématiques en particulier, des compétitions mathématiques réservées aux filles ont été créées dans certains pays où l'enseignement est mixte : la Chine en 2002 avec la China Girls Mathematical Olympiad, les États-Unis en 2009 avec le richement doté Math Prize for Girls, et l'Europe en 2012 avec l'European Girls' Math Olympiad (EGMO).
Lutter contre les stéréotypes
Quel est le but des organisateurs de telles compétitions ? Sans nul doute encourager les filles à développer leur intérêt pour les mathématiques en les plaçant dans un environnement où peut-être elles se sentiront plus à l'aise. Par exemple, le Murray Edwards College de Cambridge, au Royaume-Uni, qui a organisé la première EGMO, avait été encouragé en lançant avec succès dès 2010 la participation de filles à la China Girls Mathematical Olympiad.
On peut cependant se poser la question du bienfondé de telles compétitions, comme l'explique Michèle Artigue, professeure émérite à l'Université Paris-Diderot et ancienne présidente de l'International Commission on Mathematical Instruction (ICMI).
« Il est clair pour moi qu'il faut mener des actions pour attirer plus de filles vers les mathématiques et lutter contre les stéréotypes qui continuent à sévir, comme celles que mène notamment en France l'association Femmes et Maths […] et je me réjouis que l'Union mathématique internationale ait récemment créé un comité sur ce thème. […] En revanche, il me semble que la solution n'est absolument pas dans la séparation entre d'un côté des mathématiques pour les filles et de l'autre des mathématiques pour les garçons. Il y a tant de formes d'action possible où l'on peut favoriser la participation des filles en préservant les mixités, l'inclusion et la solidarité, je n'ai pas envie de privilégier forcément l'esprit de compétition. »
Notre interlocutrice mentionne par exemple que certains pays d'Afrique organisent déjà des camps d'excellence pour filles ou des ateliers de sensibilisation au problème du genre en mathématiques pour les enseignants de tous niveaux d'enseignement.
Les compétitions qui existent présentent des sujets intéressants, tout particulièrement EGMO, dont les énoncés font souvent preuve d'originalité, comme ceux qui suivent (EGMO 2014 et 2015 respectivement).
Alors, ces sujets : pour les filles ou pour les garçons ?
- Déterminer tous les entiers m pour lesquels le carré m×m peut être découpé en cinq rectangles dont les longueurs des côtés sont 1, 2, 3… 10 dans un certain ordre.
Pensez à évaluer le maximum et le minimum du total des aires des rectangles et vous trouverez que les seules valeurs possibles de m sont 11 et 13.
- m et n sont des entiers positifs avec m > 1. Anastasia fait de l'ensemble des entiers de 1 à 2m une partition en m paires. Boris choisit ensuite un entier de chaque paire et calcule la somme de tous ceux qu'il a choisis. Prouver qu'Anastasia peut choisir ses paires de manière que Boris ne puisse pas obtenir de somme égale à n.
Tiens, une compétition fille-garçon dans la compétition ! Voulez-vous une piste de solution ? L'idée est, à travers un certain nombre de partitions, d'éliminer toutes les valeurs possibles des sommes de Boris.
On pourra considérer pour cela trois partitions :
• La première : 1 3… 2m – 1
2 4… 2m
Ici, la somme de Boris serait comprise entre m2 et m2 + m et Alice pourra la choisir pour tous les n extérieurs à l'intervalle [m2 ; m2 + 1].
• La seconde : 1 3… m
m + 1 m + 2… 2m
On voit ici, en calculant modulo m (c'est-à-dire en ramenant les nombres à leur reste dans la division euclidienne par m), que la somme de Boris a toujours même reste dans cette division que la somme Sm de tous les entiers de 1 à m (on dit aussi que les nombres obtenus par Boris sont congrus à Sm modulo m). Les autres entiers de l'intervalle [m2 ; m2 + 1] sont inatteignables.
• On peut démontrer que c'est une troisième partition : 1 2… m
2m 2m + 1… 2m – 1
qui permettra d'éliminer les « survivants », c'est-à-dire précisément les entiers congrus à Sm modulo m.
- On pose un caillou (noir ou blanc) sur chaque sommet d'un polygone régulier à treize côtés. Prouver que l'on peut échanger la position de deux de ces cailloux de telle sorte que la couleur des cailloux soit symétrique par rapport aux axes de symétrie du polygone.
Ces treize axes de symétrie sont les diamètres passant par les treize sommets et le milieu du côté opposé. On raisonne sur le nombre n de cailloux noirs.
On peut supposer que 0 ≤ n ≤ 6, quitte à échanger « noir » et « blanc ». Les cas n = 0, 1 ou 2 sont évidents.
Pour n = 3, l'axe de symétrie à considérer passe par le milieu de l'arc formé par deux des points et on déplacera la troisième pierre au point diamétralement opposé à ce milieu. On pensera, pour n = 4, à construire un trapèze isocèle. Pour n = 5, on peut astucieusement faire jouer le principe des tiroirs : vu que les huit pierres blanches peuvent former vingt-huit paires, pour seulement treize axes de symétrie, trois d'entre elles auront même axe de symétrie. Reste une paire, c'est une de ces deux pierres qu'il faut déplacer.
D'autres problèmes ? En voici deux, le premier issu de la China Girls Mathematical Olympiad 2011 et le second du Math Prize For Girls 2014 :
- Trouver avec x ≤ y tous les entiers positifs n tels que l'équation 1/x + 1/y = 1/n ait exactement deux mille onze solutions (x, y) en entiers positifs.
- Un rectangle 4 × n (avec n un entier strictement positif) est divisé en 4n carrés unités. Chaque carré unité est colorié en blanc ou en rouge. On suppose que chaque carré unité blanc partage un côté avec au moins un carré unité rouge. Prouver qu'il y a au moins n carrés unités rouges.
L'idée pour le premier problème est de mettre l'équation sous la forme (x – n)(y – n) = n2, et le tour est joué ! On démontre que n2 doit posséder quatre-mille-vingt-et-un diviseurs, donc n doit être de la forme p2010 avec p premier.
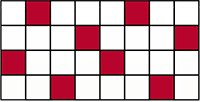
Pour le second problème, vous pouvez jouer, sur un rectangle à quatre lignes et n colonnes, à déplacer les carrés rouges, tout en conservant leur nombre et la règle du jeu, de manière à avoir au moins un carré rouge par colonne : voilà le chemin vers la solution, comme celle que voici, pour n = 8.
À la lumière des commentaires de Michèle Artigue, soulignons qu'il existe d'autres façons d'attirer les filles vers les mathématiques et de développer leur goût pour cette discipline qui nous est chère. Certaines filles – et même certains garçons – ne seraient pas porté(e)s sur la compétition ? Et alors ? Les mathématiques ne sont-elles toujours que compétition ? Pourquoi donc limiter les clubs de maths des établissement scolaires à un entraînement intensif aux Olympiades ? Pourquoi ne pas y proposer une animation autour de saines lectures d'ouvrages mathématiques, de vulgarisation (comme ceux de la Bibliothèque Tangente) ou d'autres plus académiques, des visites d'expositions ou de musées à thème mathématique, l'organisation dans l'établissement d'un évènement lié aux mathématiques, des échanges avec des mathématiciens, des visites de labos de maths, des projections de films où les maths interviennent, toutes initiatives qui se font déjà ici ou là, mais ne sont pas encore assez répandues ?
Autant de voies possibles que l'on peut tracer, en plus de celles de la compétition, pour ouvrir les jeunes esprits aux mathématiques.
Lire la suite gratuitement