Des équations pour les courbes

Une courbe paramétrée est définie par la position d’un point M(t) de la courbe en fonction d’un paramètre, souvent noté t car, historiquement, c’était le temps. Les coordonnées (x,y) du point M sont donc fonction de t : on peut écrire x = f (t) et y = g (t), où f et g sont des fonctions numériques. Selon les cas, elles sont continues, de classe C¹ (les dérivées existent et sont continues), de classe C ⁿ (les dérivées existent et sont continues jusqu’à l’ordre n), de classe C^∞ (les dérivées existent pour tous les ordres et sont donc continues) …

Si l’on veut éviter les courbes trop « pathologiques », comme celles de Peano et de Lebesgue (voir article « Donner une définition précise ? Pas si simple ! »), on ne s’intéressera qu’aux cas où  f et g sont au moins de classe C¹ sur leurs domaines de définition. Dans la pratique, la classe C² suffit, en général, pour étudier la courbe de manière satisfaisante, qu’il s’agisse du comportement local (tangente, centre et rayon de courbure, point d’inflexion…) ou de son aspect global (variations, branches infinies, convexité…). Voyons un cas particulier important. Lorsque l’on se donne une fonction f de variable réelle et à valeurs réelles, on cherche souvent à avoir sa représentation graphique, c’est-à-dire la courbe d’équation y =  f (x). Il s’agit d’un cas particulier de courbe paramétrée : une telle courbe peut en effet être définie par x (t) = t et y (t) = f (t), où t est le paramètre. L’étude d’une courbe paramétrée est relativement aisée. La dessiner, après l’étude, l’est tout autant. De plus, depuis l’avènement des outils informatiques (ordinateurs, calculatrices graphiques…), elle peut être tracée point par point, sans étude. Attention dès lors à ne pas réduire la notion de courbe paramétrée à sa représentation graphique !

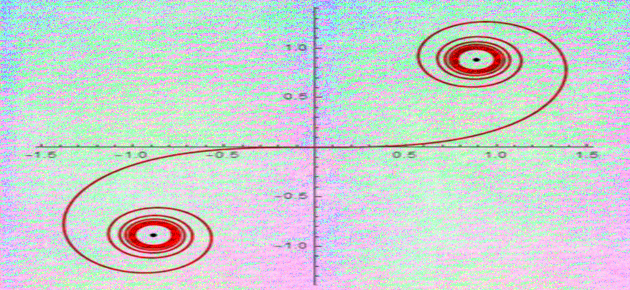
Représentation graphique de la courbe définie par
\( x(t) = \dfrac{t^3}{t^2-4}\)    et  \( y(t) = \dfrac{t(t-3)}{t-2}.\)

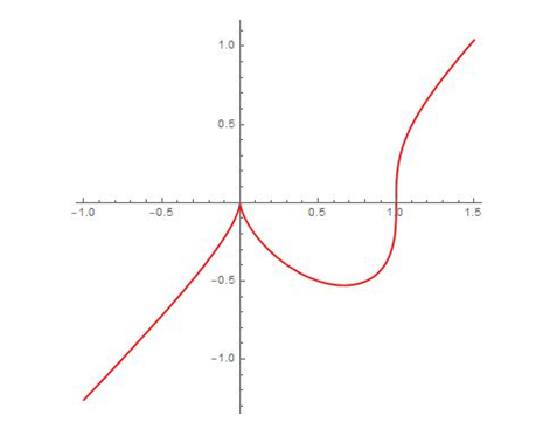
Représentation graphique de la courbe définie par  \( y= \sqrt[3]{x^2(x-1).}\)

Des points bien singuliers…

Quand le vecteur de coordonnées ( f ’(t), g’(t)) est non nul en un point M(t) d’une courbe, le point est dit régulier et ce vecteur est vecteur directeur de la tangente en M(t). Si ce vecteur est nul, le point est singulier.

Pour une courbe dont les fonctions coordonnées sont « suffisamment dérivables », le comportement local de la courbe au voisinage d’un point M( t₀), qu’il soit régulier ou singulier, est déterminé par les valeurs des dérivées successives
f ’( t₀), g’(t₀), f ’’(t₀), g’’( t₀)…

L’une des raisons de la difficulté à définir ce qu’est une « courbe » en général tient au phénomène suivant : certaines notions dépendent du paramétrage de la courbe considérée ! En effet, plusieurs paramétrages peuvent produire la même représentation graphique : cette image visuelle est souvent appelée courbe géométrique pour la distinguer de la notion de courbe paramétrée. Par exemple, un point d’une courbe peut être régulier pour un paramétrage et singulier pour un autre… même si l’aspect visuel de la courbe est le même en ce point. Ainsi, les deux paramétrages suivants définissent la même lemniscate de Bernoulli :

  \( \left( x(t) = \dfrac{\sin t}{1+ \cos^2t}, \; y(t) = \dfrac{(\sin t)(\cos t)}{1+ \cos^2 t} \right) \)  

avec 0 ≤ t ≤ 2π,

et  \( \left( x(u) = \dfrac{u+u^3}{1+ u^4}, \; y(u) = \dfrac{u-u^3}{1+ u^4} \right) \)   avec u un réel.

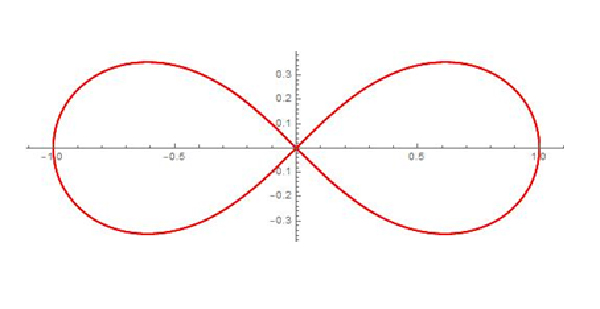
Une lemniscate de Bernoulli.

Si le passage d’un paramètre à l’autre est une application bijective de classe C¹ dont la dérivée ne s’annule pas (en terme plus savant, s’il s’agit d’un difféomorphisme), alors les propriétés géométriques des deux courbes paramétrées seront bien les mêmes. C’est le cas dans l’exemple des deux paramétrages de la lemniscate (à vérifier avec un peu de calculs…) avec u = tan( t /2).

Une courbe paramétrée est rationnelle (on dit parfois unicursale) s’il existe un paramétrage où ses composantes f et g sont des fractions rationnelles. Typiquement, la lemniscate de Bernoulli est unicursale. Toute courbe unicursale est algébrique, c’est-à-dire qu’elle admet une équation cartésienne du type P(x, y) = 0 où P est un polynôme de deux variables. On en déduit que la lemniscate de Bernoulli est une courbe algébrique. C’est en fait une quartique ; son équation cartésienne est (x ² + y ²)² – (x ² – y ²) = 0.

[encadre]

Les coordonnées polaires

Dans le plan habituel, une fois un système orthonormé de coordonnées choisi, un point est repéré par ses coordonnées (x, y) où x est l’abscisse et y l’ordonnée.

Mais on peut aussi repérer un point par ses coordonnées polaires ρ et θ, où θ est l’angle que fait l’axe (Ox) avec le vecteur  \( \overrightarrow{\text{OM}}\) et la valeur absolue | ρ | de ρ est la longueur OM. Le changement de coordonnées est donné par les formules x = ρ cos θ et y = ρ sin θ .

L’intérêt de ce changement de repère est qu’il existe des techniques particulières pour étudier les courbes en coordonnées polaires.

[/encadre]

On peut aussi définir une courbe paramétrée en coordonnées polaires : on donne ρ en fonction de l’angle θ, soit ρ = ρ(θ ). Cela revient à définir la courbe, avec θ comme paramètre, par x = ρ(θ ) cos θ et y = ρ(θ ) sin θ.

Ainsi, si  \( \rho = \dfrac{\theta}{\theta -1}, \) on a la courbe ci-dessous. En noir figure une droite asymptote (quand θ tend vers 1) et un cercle asymptote (lorsque θ tend vers l’infini).

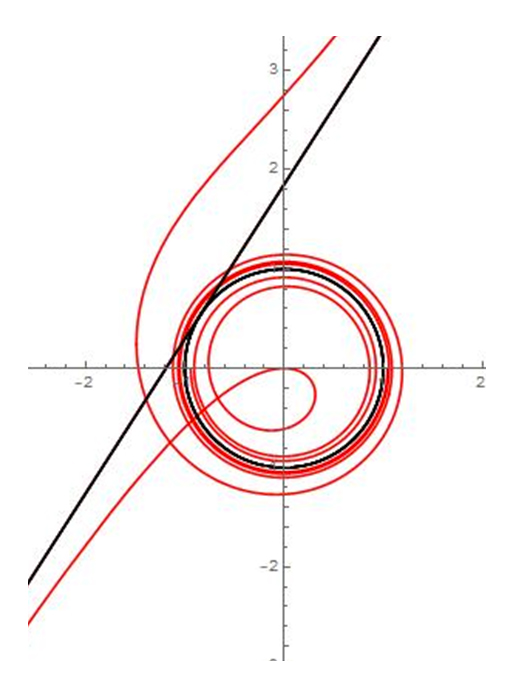
Autant il est, en général, assez facile de tracer une courbe paramétrée, autant il est plus difficile de déterminer si un point particulier y appartient. Pour savoir si le point M₀ de coordonnées ( x₀, y₀) appartient à la courbe paramétrée définie par x = f (t) et y = g (t), il faut résoudre le système d’équations suivant, où t est l’inconnue : x₀ = f (t) et y₀ = g (t). Cela n’est pas toujours évident, ni même possible…

Une équation cartésienne

Une équation cartésienne (appelée aussi équation implicite) d’une courbe est du type f (x, y) = 0, où f est une fonction numérique (c’est-à-dire à valeurs dans ℝ) de deux variables. Au minimum, f doit être continue. Il est préférable qu’elle soit de classe C¹ (c’est-à-dire que les deux dérivées partielles, par rapport à chacune des variables, existent et sont continues) pour éviter les courbes « pathologiques » et pour avoir l’existence de tangentes.

La classe C² (c’est-à-dire que les dérivées partielles existent jusqu’à l’ordre 2 et sont continues) pour f donnera des courbes « plus régulières » ; il sera alors plus aisé de calculer de nombreuses caractéristiques de la courbe (points d’inflexion, rayon et centre de courbure…).

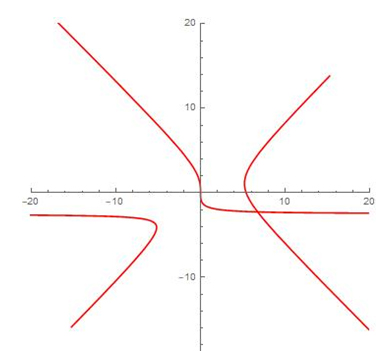
Prenons la représentation de la courbe d’équation (x ² + y ² – 1)³ – x ²y ³ = 0. Il s’agit d’une sextique (courbe algébrique de degré 6), que l’on appelle le cœur d’Eugène Beutel, du nom de celui qui, sans doute, l’a dessinée pour la première fois, en 1907, dans un ouvrage sur les courbes algébriques.

Quand  f est un polynôme en x et y (comme dans l’exemple précédent), la courbe est dite algébrique. De nombreux mathématiciens, depuis René Descartes et Pierre de Fermat au XVII ^e siècle, puis Isaac Newton, se sont intéressés à ces courbes qui sont de classe C ^∞.

Toutes les courbes algébriques peuvent être construites, au moins par morceaux, par un système composé d’un nombre fini de tiges rectilignes rigides articulées entre elles ou à des points fixes. La réciproque est aussi vraie (voir Tangente 176, 2017). C’est un résultat de 1875 démontré par Alfred Kempe (1849 – 1922), connu aussi pour ses recherches sur le théorème des quatre couleurs.

Voilà une courbe qui n’est pas algébrique : la spirale de Fermat. Son équation est
x sin( x ² + y ²) – y cos( x ² + y ²) = 0. Elle a été étudiée par Ménélaüs d’Alexandrie à la fin du Ier siècle et par Fermat en 1636.

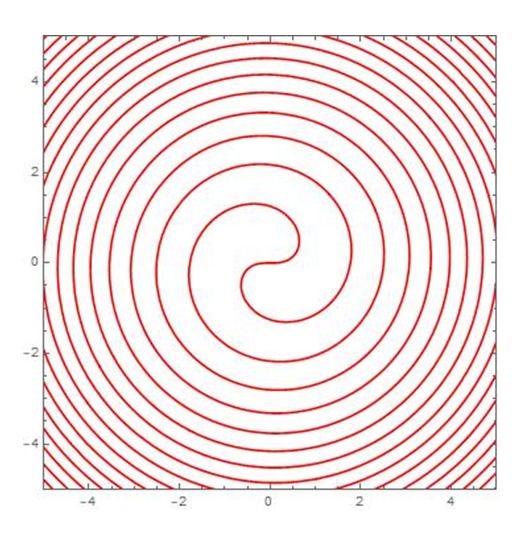
Revenons au cas général d’une courbe définie à l’aide d’une équation cartésienne. Il est alors facile de vérifier qu’un point donné de coordonnées ( x₀, y₀) y appartient. Il suffit simplement de calculer f (x₀, y₀) et de vérifier que cette valeur est nulle ! Par contre, en général, il est plus difficile de la construire…

L’intérêt de l’implicite

Pourtant, on dispose d’un théorème local, le théorème des fonctions implicites, qui nous indique qu’au voisinage d’un point M₀ de coordonnées ( x₀, y₀) de la courbe tel que la dérivée partielle  \( \dfrac{\partial f}{\partial y} (x_0, y_0)\)  ne s’annule pas, il existe une fonction ϕ d’une variable réelle définie sur un voisinage V de x₀ telle que « f  (x, y) = 0 » soit équivalent à « y = ϕ (x) ». Autrement dit, au voisinage d’un tel point M₀, la courbe est la représentation graphique d’une fonction numérique de classe C¹. Ce théorème donne, par exemple, une formule pour calculer les points d’inflexion de la courbe ou la courbure en un point. Mais il est de peu d’utilité pour la construction effective de la courbe.

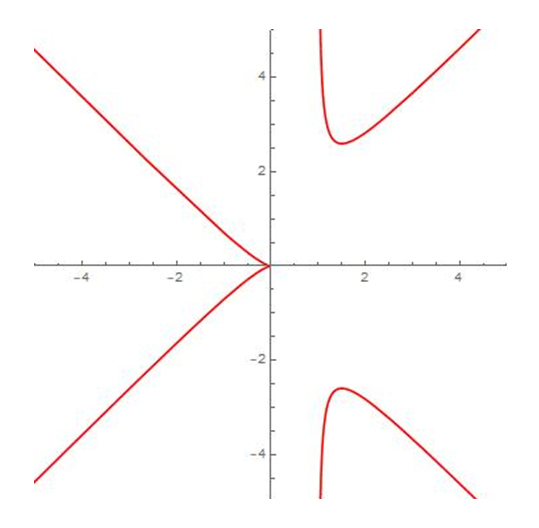
Il n’y a pas de méthode générale ! Après l’étude des branches infinies, on peut, par exemple, chercher les points situés sur des droites verticales (x constant) et horizontales (  y constant). On peut essayer de paramétrer la courbe : par exemple si elle passe par l’origine O, on étudie l’intersection avec les droites passant par O, d’équation y = tx.

Par exemple, considérons la cubique d’équation y ²(x – 1) – x ³ = 0. Elle passe par le point O. Considérons les points de la courbe situés sur la droite d’équation y = t x autres que O. Ils vérifient t ²x ²(x – 1) – x ³ = 0, d’où l’on tire  \( x= \dfrac{t^2}{t^2 -1}\) et  \( y= \dfrac{t^3}{t^2 -1}.\)

La construction de la courbe s’en déduit.

Plus subtil, une équation intrinsèque

Voyons un cas plus subtil, celui d’une équation intrinsèque. Il s’agit de décrire une courbe par une équation utilisant exclusivement les invariants de la géométrie différentielle : l’abscisse curviligne (associée à la longueur) et le rayon de courbure, respectivement notés s et R. La courbe est alors définie à un déplacement près : en effet, un déplacement du plan (rotation ou translation) ne modifie ni l’abscisse curviligne, ni la courbure en un point quelconque.

La courbe définie par l’équation R s = 1 est la clothoïde (appelée aussi spirale d’Euler ou spirale de Cornu). Elle a été étudiée dès 1705 par Jacques Bernoulli et, en 1743, par Leonhard Euler. Elle tient l’un de ses noms du physicien français Alfred Cornu (1841 – 1902). De nos jours, elle trouve des applications techniques dans le tracé des voies ferroviaires et routières et aussi en conception assistée par ordinateur (CAO).

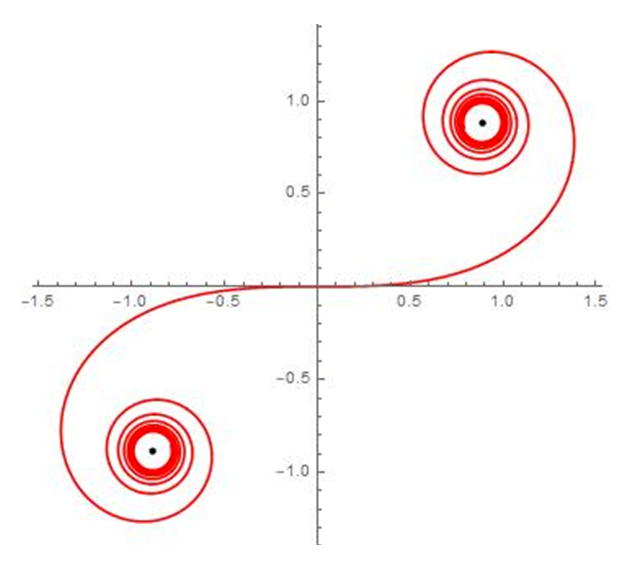
La clothoïde.

La clothoïde admet aussi une représentation paramétrique :

  \( \left \{ \begin{array}{l} x=\sqrt{2} \int^t_0 \cos (u^2) du, \\[2mm] y=\sqrt{2} \int^t_0 \sin (u^2) du. \end{array} \right.\)  

Euler a mis trente-cinq ans pour obtenir les coordonnées des points asymptotes.

Ici, ce sont  \( \left( \dfrac{\sqrt{\pi}}{2}, \dfrac{\sqrt{\pi}}{2}\right) \)  et  \( \left( -\dfrac{\sqrt{\pi}}{2}, -\dfrac{\sqrt{\pi}}{2}\right) .\)

Comme quoi, l’étude des courbes réserve encore bien des surprises et des sources d’émerveillement à l’amateur de géométrie !