
Après l’« invention » par René Descartes, dans son ouvrage fondamental Géométrie (1637), de la géométrie analytique, avec l’introduction des coordonnées, et les travaux de Pierre de Fermat à la même époque, les mathématiciens ont étudié de manière systématique les courbes définies par une équation du type P(x, y) = 0, où P est un polynôme en deux variables. Dénommées courbesgéométriques par Descartes, elles sont appelées maintenant courbesalgébriques. Par exemple, la courbe algébrique donnée par l’équation x 2 + 2 y 2 − 2 x − 2 = 0 est une ellipse. Celle définie par y 2 (1 + x) = x 2 (1 − x) est une cubique particulière : c’est une strophoïde. On y voit un point double. La courbe d’équation (x 2 + y 2 − 1)3 − x 2 y 3 = 0 est une sextique : c’est le cœur de Beutel. On y devine deux points de rebroussement.
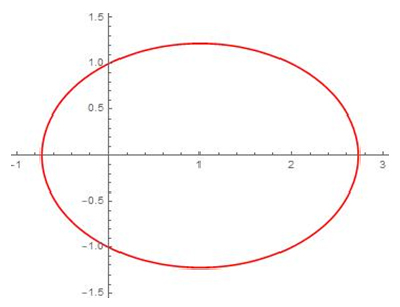
Une ellipse.

Une strophoïde.
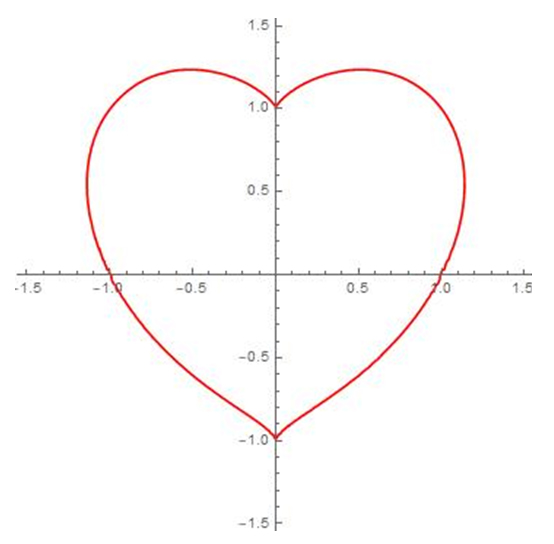
Le cœur de Beutel.
Quand les degrés montent…
Les courbes algébriques sont classées selon le degré du polynôme P. Or, si l’on élève P au carré, l’équation correspondante produit la même courbe que celle définie par P (x, y) = 0, mais le degré n’est alors plus le même ! De manière générale, on supposera que le polynôme P ne contient pas de facteur carré. Dans ce cas, le degré du polynôme est le degré de la courbe algébrique.
Si le degré de P est 1, P (x, y) = a x + b y + c : l’équation associée est celle d’une droite. Si le degré de P est 2, P(x, y) = a x 2 + b x y + c y 2 + d x + e y + f : l’équation associée est celle d’une conique. Selon les coefficients, ce sera une ellipse, une parabole, ou une hyperbole, ou elle sera dégénérée (en un cercle, deux droites, une droite, voire un ensemble − qui peut être vide − de points). De fait, les courbes algébriques sont classées selon leur degré.

Dans le plan affine réel ℝ2, le nombre maximum de points d’intersection d’une courbe algébrique avec une droite est un minorant du degré de la courbe et lui est très souvent égal. Par exemple, si l’on prend une parabole, le nombre de points d’intersection avec une droite est égal à 0 si la droite ne coupe pas la parabole (en orange), 1 si la droite est tangente à la parabole (en vert) ou la coupe selon la direction de son axe (en bleu), 2 si elle la coupe transversalement à son axe (en violet).
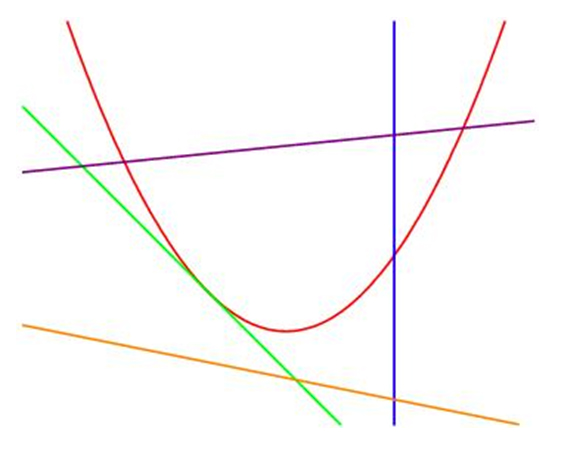
Le maximum est donc 2 : c’est le degré de l’ellipse en tant que courbe algébrique. Pour la droite (en vert) tangente à la parabole, on peut considérer que le point d’intersection est double (on peut voir la tangente comme position limite d’une sécante), donc dire qu’il y a deux points d’intersection. Dans le cas où la droite (en bleu) est parallèle à l’axe de la parabole, en plus du point d’intersection avec la parabole, on peut considérer que la droite et la parabole ont un « point commun à l’infini » (c’est ce qu’il se passerait si, au lieu de considérer la parabole dans le plan affine, on l’étudiait dans le plan projectif réel).
Pour trouver les coordonnées des points d’intersection de la parabole avec une droite non parallèle à son axe, on peut résoudre le système des deux équations y = x 2 et y = a x + b. On a alors, selon le signe du discriminant de l’équation du second degré obtenue en éliminant y, deux solutions, ou une solution double, ou aucune. On retrouve alors ce que l’on voit graphiquement. En considérant les deux équations dans l’ensemble des nombres complexes, il y a toujours deux solutions (ou une solution double) : dans le plan complexe projectif, l’intersection d’une droite et d’une parabole est toujours constituée de deux points, l’un étant éventuellement à l’infini.
En fait, dans le plan projectif complexe, une droite coupe une courbe algébrique de degré n en exactement n points. C’est Jean-Victor Poncelet (1788 – 1867) qui, en 1822 dans son Traité des propriétés projectives des figures, a introduit ce point de vue unificateur.
Si l’on se place dans le plan affine habituel ou dans le plan projectif réel, la valeur obtenue est un maximum. On retrouve cette situation dans de nombreux résultats sur les courbes algébriques. Dans le plan projectif complexe, la valeur est toujours prise… C’est plus simple !
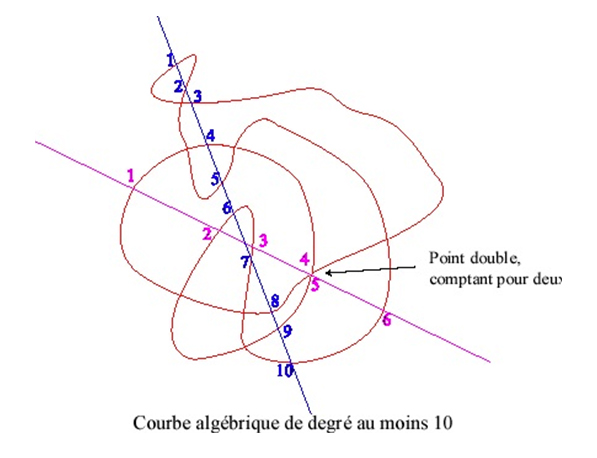
À l’intersection
Un autre problème, très vite abordé au XVIII e siècle, est celui de l’intersection de deux courbes algébriques de degrés respectifs m et n. Le mathématicien écossais Colin MacLaurin (1698 – 1746) a conjecturé dès 1720 qu’en général le nombre de points d’intersection de ces deux courbes est égal au produit mn. Les mathématiciens suisses Gabriel Cramer (1704 – 1752) puis Leonhard Euler (1707 – 1783) s’y sont intéressés ; ce dernier se rend compte des difficultés liées à la présence dans les équations de racines multiples ou de racines dont les valeurs ne sont pas réelles.
[encadre]
Le paradoxe de Cramer
Dans une lettre adressée à Leonhard Euler en 1744, Gabriel Cramer soulevait le problème que neuf points déterminent une cubique de manière unique et que, deux cubiques se coupant en 3 × 3 = 9 points, par ces neuf points, il passe deux cubiques. Cela semble contradictoire.
Euler travailla sur la question et sa réponse fut publiée en 1748. Sans avoir les concepts de l’algèbre linéaire, découverts au cours du XIX e siècle, le génial mathématicien explique que, dans le cas des neuf points d’intersection, ces points ne sont pas quelconques et le système des équations linéaires qu’il faut résoudre n’admet pas de solution unique car les équations ne sont pas indépendantes (en termes plus modernes, le système linéaire n’est pas de rang maximal). Le paradoxe était résolu et le décor planté pour la naissance de la théorie des déterminants et l’invention de l’algèbre linéaire !

[/encadre]
En 1764, Étienne Bézout (1730 – 1783) démontre, dans des cas simples, le résultat conjecturé par MacLaurin. En fait, il prouve que deux courbes algébriques sans composantes communes respectivement de degré m et de degré n possèdent au plus mn points d’intersection. Pour avoir l’égalité, il faut considérer les courbes dans l’espace projectif complexe et tenir compte des multiplicités.
Combien de points distincts sont-ils nécessaires pour définir une courbe algébrique ? Pour une droite, la réponse est évidemment 2. Pour un cercle, la réponse est 3. Malheureusement, trois points ne permettent pas de définir une unique ellipse. Quatre non plus ! Alors, combien de points pour déterminer une ellipse ?
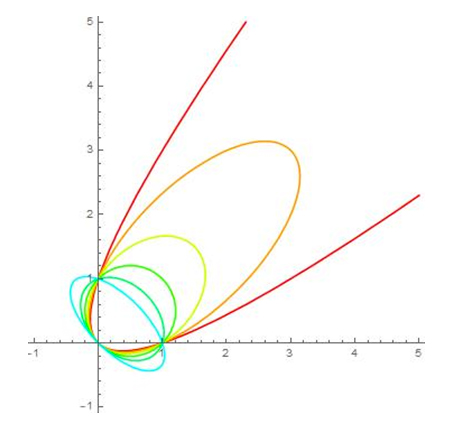
Toutes ces ellipses passent par les trois mêmes points.
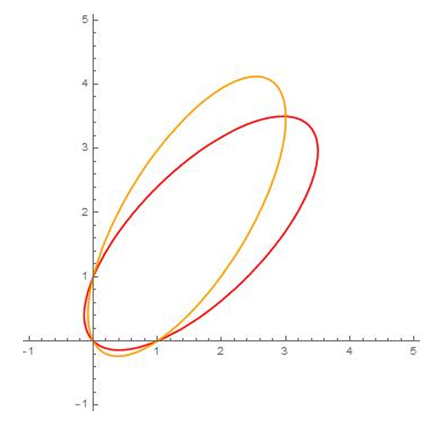
Ces ellipses passent par les quatre mêmes points.
Prenons une courbe algébrique définie par une équation P(x, y) = 0 où P est un polynôme des deux variables x et y. Le degré de P étant n, P s’écrit comme une somme de termes du type ax h y k avec les trois relations 0 ≤ h ≤ n, 0 ≤ k ≤ n et 0 ≤ h + k ≤ n. Pour chaque valeur de h, k peut prendre n − h + 1 valeurs, ce qui donne (n + 1) + n + (n − 1) +… + 1 termes possibles. Cette somme de tous les entiers de 1 à n + 1 vaut
Le polynôme P étant déterminé à une constante multiplicative près, le nombre Cn de coefficients « libres » est donc égal à
Pour déterminer une courbe algébrique de degré n, il faut se donner Cn points et résoudre alors un système de Cn équations linéaires à Cn inconnues (les coefficients du polynôme P). Pour une ellipse, qui est une courbe de degré 2, la réponse est donc cinq points : cinq points définissent une ellipse… s’il en existe une passant effectivement par ces points ! Car le calcul précédent indique que par cinq points distincts passe une unique conique, pas obligatoirement une ellipse. En outre, on peut avoir des cas particuliers : si les cinq points sont alignés, la conique est une droite double ! Et il ne faut pas oublier que tout ceci se passe dans le plan projectif complexe. Ce qui explique au passage qu’il suffit de trois points non alignés pour déterminer un cercle : tous les cercles du plan (projectif complexe) passent par les deux points cycliques (qui sont deux points à l’infini) introduits par Poncelet. D’ailleurs, on pourrait définir un cercle comme une conique passant par ces deux points cycliques !
D’un trait de crayon
Les courbes rationnelles (voir encadré) sont aussi appelées unicursales. Étymologiquement, « unicursal » veut dire que l’on peut tracer la courbe d’un trait de crayon : elle possède une seule composante connexe. En fait, une courbe rationnelle possède bien une seule composante connexe… dans l’espace projectif complexe ! L’hyperbole est particulièrement trompeuse avec ses deux branches qui se rejoignent à l’infini et ne forment donc qu’une seule composante connexe.
Mais la réciproque est fausse : une courbe qui ne possède qu’une seule composante connexe (unipartite) n’est pas obligatoirement rationnelle.
L’étude des courbes algébriques, les concepts introduits pour surmonter les difficultés (par exemple les notions de composante ou de multiplicité d’intersection) puis les généralisations à des espaces différents sont à la base d’une branche des mathématiques en plein essor au cours du XX e siècle : la géométrie algébrique, au carrefour de la géométrie, de l’algèbre et de l’arithmétique.
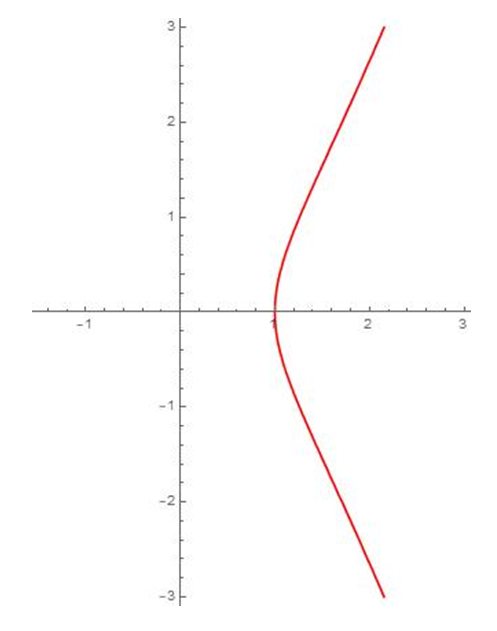
Cette cubique d’équation y 2 – x 3 + 1 = 0 ne possède qu’une seule composante connexe mais n’est pas unicursale.
[encadre]
Des courbes rationnelles… ou non
On appelle courbes rationnelles les courbes d’équations
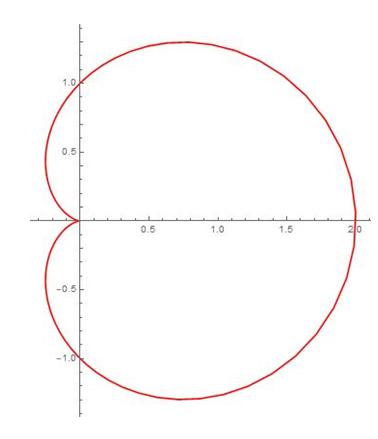
La cardioïde est une courbe rationnelle ;
ses équations sont
En éliminant t, on obtient l’équation (x 2 + y 2 − x)2 = x 2 + y 2 qui montre que c’est une quartique.
Toute courbe rationnelle est algébrique : son degré est le plus grand des degrés des polynômes P, Q et R à condition que la représentation soit propre, c’est-à-dire que chaque point de la courbe, à l’exception d’un nombre fini d’entre eux, ne soit obtenu que pour une seule valeur du paramètre. Se pose la question de la réciproque : une courbe algébrique est-elle rationnelle ? Les courbes algébriques de degrés 1 et 2 sont rationnelles mais la réponse est négative en général. En fait, on peut définir un invariant géométrique associé à la courbe, le genre, qui est un entier positif. On montre alors qu’une courbe est rationnelle si, et seulement si, son genre est égal à 0.
Le calcul du genre n’est pas toujours évident mais, pour une courbe régulière (sans point double ni point de rebroussement) de degré n, il est égal à
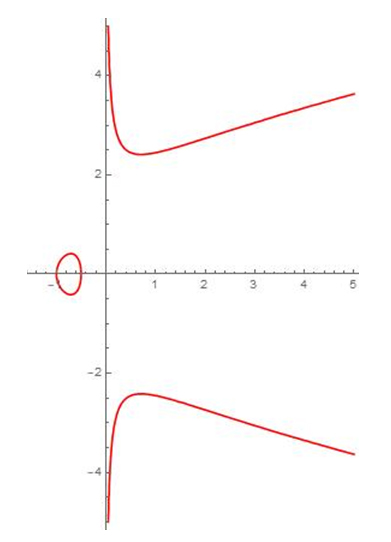
Cubique d’équation x y 2 – (x + 1)(2x + 1) = 0, et qui n’est pas rationnelle.
[/encadre]
Lire la suite